1控制系统的校正
系统性能
稳定性、准确性、快速性
动态性能-超前校正
阶跃曲线、频域(bode图)、根轨迹(增加零点-根轨迹左移稳定性提高)、PID控制(PD)
静态性能-滞后校正
阶跃曲线、频域(bode图)、根轨迹(增加极点-根轨迹右移稳定性提高)、PID控制(PI)
2系统模型
超前校正未校正系统模型:
超前校正:增加一对零极点,使得零点更靠近坐标原点
滞后校正未校正系统模型:
滞后校正:增加一对零极点,使得极点更靠近坐标原点
3运行效果分析
3.1未校正
num=[4];
den=[conv([1 0],[1 2])];
G=tf(num,den)
G1=feedback(G,1)
figure(1)
step(G1)
figure(2)
bode(G)
grid on阶跃响应

伯德图
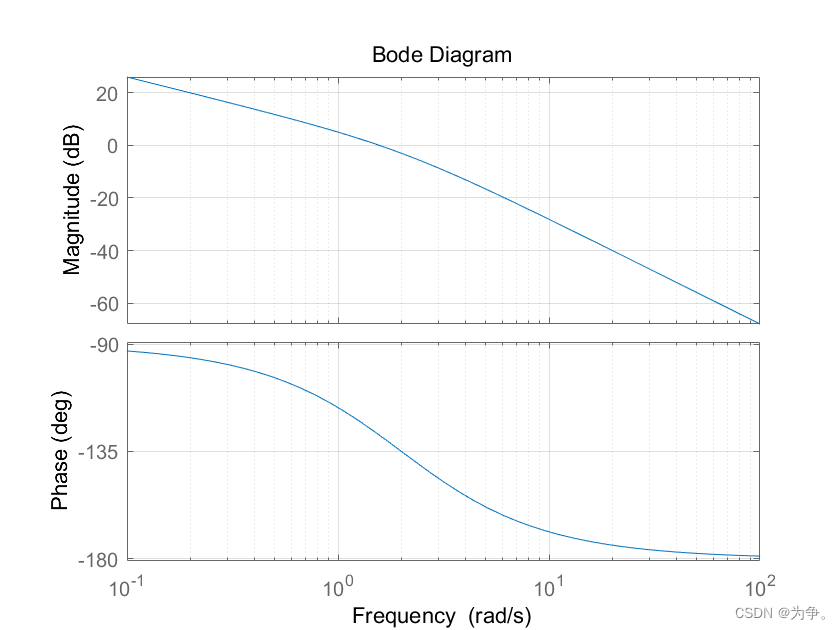
3.2 使用第一个函数进行超前校正
num=[4];
den=[conv([1 0],[1 2])];
G=tf(num,den)
G1=feedback(G,1)
num1=[18.7 18.7*2.9];
den1=conv(conv([1 0],[1 2]),[1 5.4])
G2=tf(num1,den1)
G3=feedback(G2,1)
figure(1)
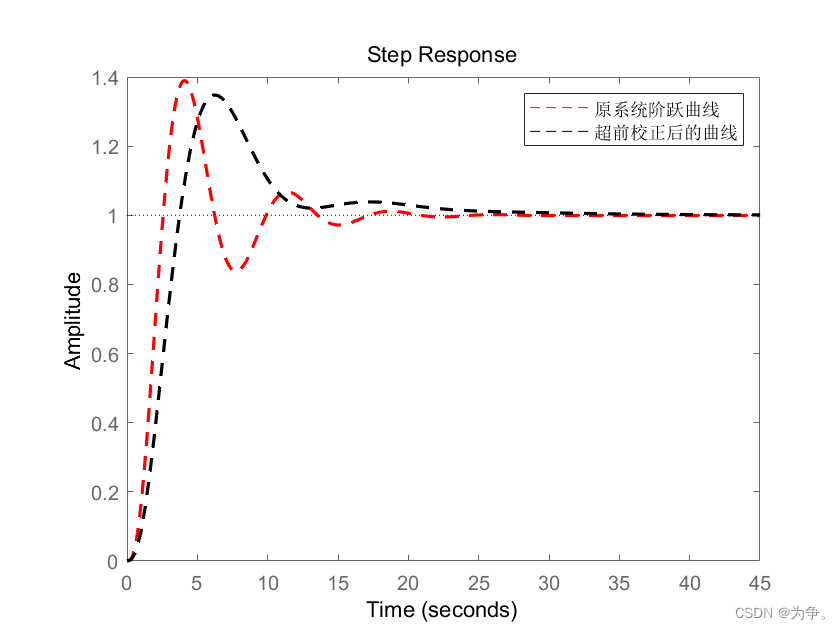
step(G1,'r--',G3,'k--')
legend('原系统阶跃曲线','超前校正后的曲线')
figure(2)
bode(G,'r--',G2,'k--')
legend('原系统阶跃曲线','超前校正后的bode曲线')
figure(3)
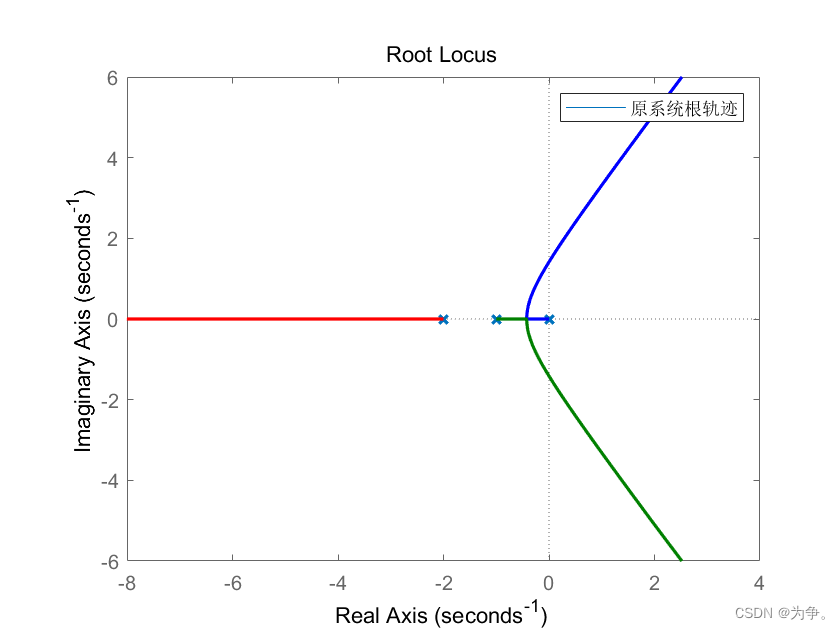
rlocus(G)
legend('原系统根轨迹')
figure(4)
rlocus(G2)
legend('校正后根轨迹')
set(findobj('Type','line'),'LineWidth',1.6)阶跃响应:由图可知系统阶跃响应的稳定性、准确性和快速性都有了提升。

根轨迹:超前校正增加了零点,根轨迹左偏,稳定性增加
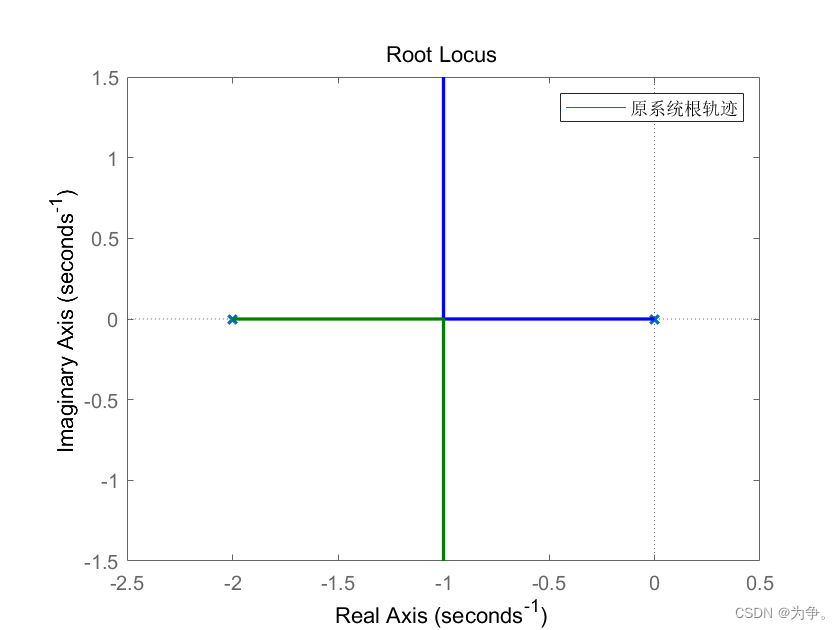
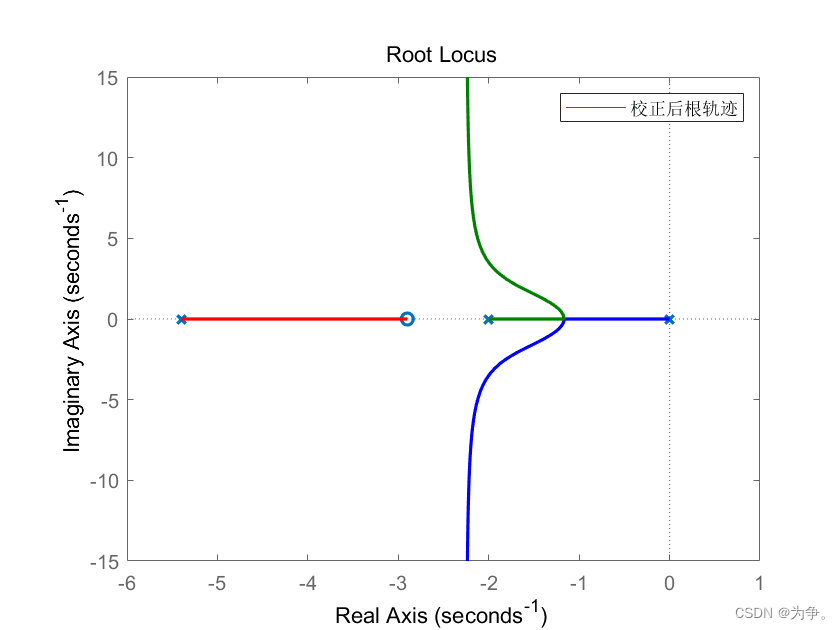
Bode图:开环增益越高,稳态误差减小,系统性能越好,即相频特性中初始值抬高。Wc增大,y值增大,即在相频特性纵坐标为0时,幅频特性曲线越高,说明系统的性能越好。
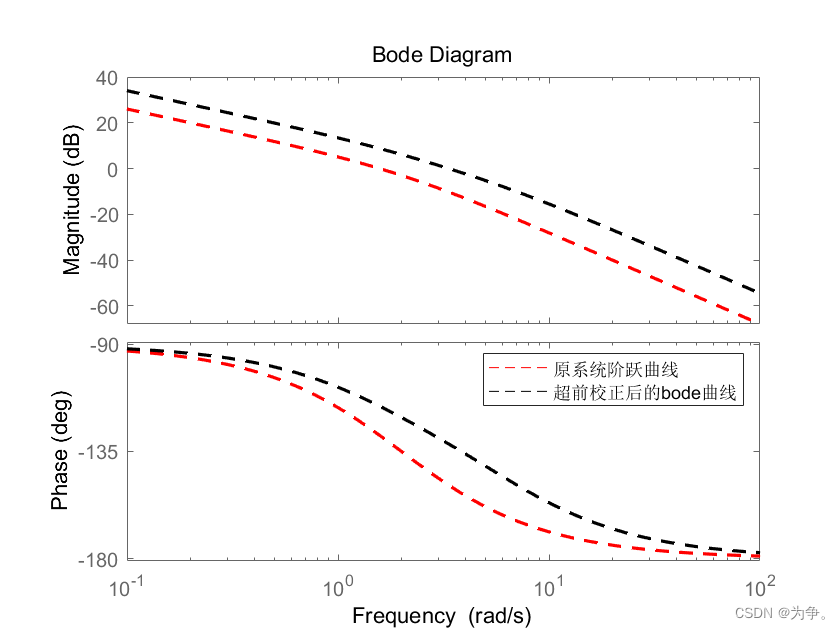
3.3 使用第二个函数进行超前校正
与第一个系统进行对比,系统是更稳定的。增加一对零极点,使零点更靠近坐标原点,零点和极点的值越大,系统性能越好
num=[4];
den=[conv([1 0],[1 2])];
G=tf(num,den)
G1=feedback(G,1)
num1=[41.7 41.7*4.41];
den1=conv(conv([1 0],[1 2]),[1 18.4])
G2=tf(num1,den1)
G3=feedback(G2,1)
figure(1)
step(G1,'r--',G3,'k--')
legend('原系统阶跃曲线','超前校正后的曲线')
figure(2)
bode(G,'r--',G2,'k--')
legend('原系统阶跃曲线','超前校正后的bode曲线')
figure(3)
rlocus(G)
legend('原系统根轨迹')
figure(4)
rlocus(G2)
legend('校正后根轨迹')
set(findobj('Type','line'),'LineWidth',1.6)
grid on
[a1,b1,c1,d1]=margin(G)
[a2,b2,c2,d2]=margin(G2)3.4滞后校正
num=[1];
den=conv(conv([1 0],[0.5 1]),[1 1])
G=tf(num,den)
G1=feedback(G,1)
num1=[5*10 5*1];
den1=conv(conv([1 1 0],[0.5 1]),[100 1])
G2=tf(num1,den1)
G3=feedback(G2,1)
figure(1)
step(G1,'r--',G3,'k--')
legend('原系统阶跃曲线','超前校正后的曲线')
figure(2)
bode(G,'r--',G2,'k--')
legend('原系统阶跃曲线','超前校正后的bode曲线')
figure(3)
rlocus(G)
legend('原系统根轨迹')
figure(4)
rlocus(G2)
legend('校正后根轨迹')
set(findobj('Type','line'),'LineWidth',1.6)
grid on
[a1,b1,c1,d1]=margin(G)
[a2,b2,c2,d2]=margin(G2)阶跃响应:没有太大区别
根轨迹:滞后校正增加极点,根轨迹右偏,稳定性增加
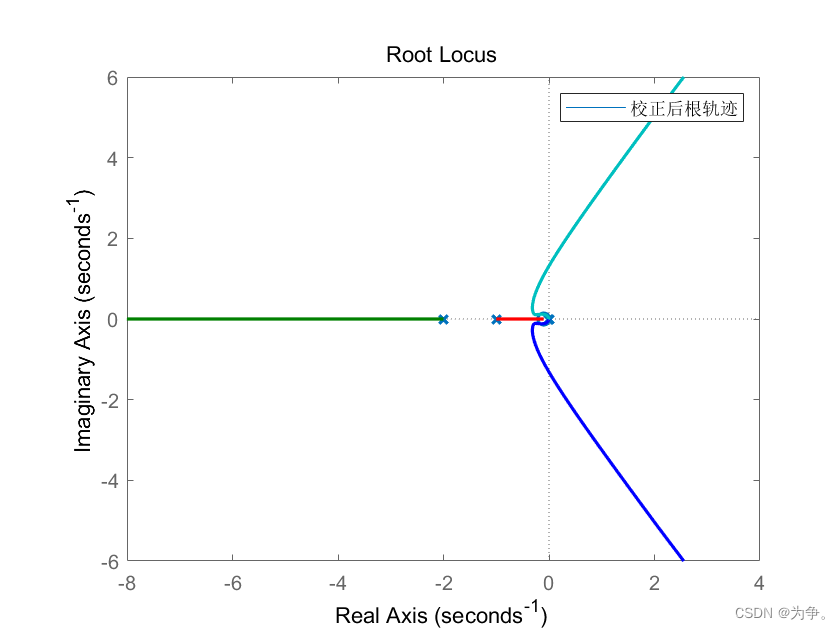
频域响应Bode图:开环增益越高,稳态误差减小,系统性能越好,即相频特性中初始值抬高,Wc增大。y值增大,即在相频特性纵坐标为0时,幅频特性曲线越高,说明系统性能越好。

整理自:【自控】快速搞定超前-滞后校正的原理及Matlab仿真验证_哔哩哔哩_bilibili