🔎大家好,我是Sonhhxg_柒,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流🔎
📝个人主页-Sonhhxg_柒的博客_CSDN博客 📃
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏 - 机器学习【ML】 自然语言处理【NLP】 深度学习【DL】
🖍foreword
✔说明⇢本人讲解主要包括Python、机器学习(ML)、深度学习(DL)、自然语言处理(NLP)等内容。
如果你对这个系列感兴趣的话,可以关注订阅哟👋
文章目录
设置Mountain Car环境playground
做好准备
怎么做...
这个怎么运作...
用梯度下降近似估计 Q 函数
怎么做...
这个怎么运作...
也可以看看
使用线性函数逼近开发 Q 学习
怎么做...
这个怎么运作...
使用线性函数逼近开发 SARSA
怎么做...
这个怎么运作...
使用经验回放合并批处理
怎么做...
这个怎么运作...
使用神经网络函数逼近开发 Q-learning
怎么做...
这个怎么运作...
也可以看看
用函数逼近解决 CartPole 问题
怎么做...
这个怎么运作...
到目前为止,我们已经在 MC 和 TD 方法中以查找表的形式表示了值函数。TD 方法能够在一个 episode 中动态更新 Q 函数,这被认为是 MC 方法的进步。然而,TD 方法对于具有许多状态和/或动作的问题仍然没有足够的可扩展性。使用 TD 方法为单个状态和动作对学习太多值会非常慢。
本章将重点介绍函数逼近,它可以克服 TD 方法中的缩放问题。我们将从设置 Mountain Car 环境游乐场开始。开发线性函数估计器后,我们会将其纳入 Q-learning 和 SARSA 算法。然后,我们将使用经验回放改进 Q-learning 算法,并尝试使用神经网络作为函数估计器。最后,我们将介绍如何使用我们在本章中学到的知识来解决 CartPole 问题。
本章将介绍以下食谱:
- 设置Mountain Car环境playground
- 用梯度下降近似估计 Q 函数
- 使用线性函数逼近开发 Q 学习
- 使用线性函数逼近开发 SARSA
- 使用经验回放合并批处理
- 使用神经网络函数逼近开发 Q-learning
- 用函数逼近解决 CartPole 问题
设置Mountain Car环境playground
TD 方法可以在一集中学习 Q 函数,但不可扩展。例如,象棋游戏中的状态数约为 1,040,而围棋游戏中的状态数约为 1,070。此外,使用 TD 方法学习连续状态的值似乎是不可行的。因此,我们需要使用函数逼近 (FA)来解决此类问题,它使用一组特征来逼近状态空间。
在第一个秘籍中,我们将从熟悉 Mountain Car 环境开始,我们将在接下来的秘籍中借助 FA 方法解决这个问题。
Mountain Car ( https://gym.openai.com/envs/MountainCar-v0/ ) 是一个典型的具有连续状态的 Gym 环境。如下图所示,它的目标是让小车到达山顶:

在一维轨道上,汽车位于 -1.2(最左边)和 0.6(最右边)之间,目标(黄旗)位于 0.5。汽车的发动机不够强劲,无法一次将其推上山顶,因此它必须来回行驶以积蓄动力。因此,每个步骤都有三个独立的操作:
- 向左推 (0)
- 没有推动 (1)
- 向右推 (2)
环境有两种状态:
- 汽车的位置:这是一个从 -1.2 到 0.6 的连续变量。
- 汽车的速度:这是一个从 -0.07 到 0.07 的连续变量。
与每一步相关的奖励为 -1,直到汽车到达目标(位置为 0.5)。
当汽车到达目标位置(显然)或 200 步后,一集结束。
做好准备
要运行 Mountain Car 环境,我们首先在环境表中搜索它的名称 – Table of environments · openai/gym Wiki · GitHub。我们得到MountainCar-v0并知道观察空间由两个浮点数表示,并且存在三种可能的操作(左 = 0,不推 = 1,右 = 2)。
怎么做...
让我们按照以下步骤模拟 Mountain Car 环境:
1.我们导入 Gym 库并创建 Mountain Car 环境的实例:
>>> import gym
>>> env = gym.envs.make("MountainCar-v0")
>>> n_action = env.action_space.n
>>> print(n_action)
32.重置环境:
>>> env.reset()
array([-0.52354759, 0. ])汽车以状态 开始[-0.52354759, 0.],这意味着初始位置约为 -0.5,速度为 0。您可能会看到不同的初始位置,因为它是从 -0.6 到 -0.4 随机生成的。
3.现在让我们采取一种天真的方法:我们只是继续将汽车向右推,并希望它能到达顶部:
>>> is_done = False
>>> while not is_done:
... next_state, reward, is_done, info = env.step(2)
... print(next_state, reward, is_done)
... env.render()
>>> env.render()
[-0.49286453 0.00077561] -1.0 False
[-0.4913191 0.00154543] -1.0 False
[-0.48901538 0.00230371] -1.0 False
[-0.48597058 0.0030448 ] -1.0 False
......
......
[-0.29239555 -0.0046231 ] -1.0 False
[-0.29761694 -0.00522139] -1.0 False
[-0.30340632 -0.00578938] -1.0 True4.关闭环境:
env.close()这个怎么运作...
在第 3 步中,状态(位置和速度)不断变化,每一步的奖励为 -1。
您还会在视频中看到汽车反复向右和向左移动,但最终没有到达顶部:

可以想象,Mountain Car 问题并不像您想象的那么简单。我们需要来回驾驶汽车以增强动力。而且状态变量是连续的,也就是说一个表lookup/update方法(比如TD方法)是行不通的。在下一个秘籍中,我们将使用 FA 方法解决 Mountain Car 问题。
用梯度下降近似估计 Q 函数
从这个秘籍开始,我们将开发 FA 算法来解决具有连续状态变量的环境。我们将从使用线性函数和梯度下降逼近 Q 函数开始。
FA的主要思想 是使用一组特征来估计 Q 值。这对于 Q 表变得巨大的状态空间很大的进程非常有用。有几种方法可以将特征映射到 Q 值;例如,线性近似是特征和神经网络的线性组合。使用线性近似,动作的状态值函数由特征的加权和表示:
![]()
这里,F1(s),F2(s),……,Fn(s)是给定输入状态s的一组特征;θ1, θ2,......, θn 是应用于相应特征的权重。或者我们可以把它写成 V(s)=θF(s)。
正如我们在 TD 方法中看到的那样,我们有以下公式来计算未来状态:
![]()
这里,r 是从状态 st 转换到 st+1 所获得的相关奖励,α 是学习率,γ 是折扣因子。让我们将 δ 表示为 TD 误差项,现在我们有以下内容:

这是梯度下降的确切形式。因此,学习的目标是找到最佳权重 θ,以最好地近似每个可能动作的状态值函数 V(s)。我们在这种情况下试图最小化的损失函数类似于回归问题中的损失函数,它是实际值和估计值之间的均方误差。在一个 episode 中的每一步之后,我们都会对真实状态值进行新的估计,然后我们将权重 θ 移动到它们的最佳值。
需要注意的另一件事是给定输入状态 s 的特征集 F(s)。一个好的特征集是可以捕获不同输入的动态的特征集。通常,我们可以在各种参数(包括均值和标准差)下使用一组高斯函数生成一组特征。
怎么做...
我们开发了基于线性函数的 Q 函数逼近器,如下所示:
1.导入所有必要的包:
>>> import torch
>>> from torch.autograd import Variable
>>> import math该变量包装了一个张量并支持反向传播。
2.然后,启动__init__method 线性函数的Estimator类:
>>> class Estimator():
... def __init__(self, n_feat, n_state, n_action, lr=0.05):
... self.w, self.b = self.get_gaussian_wb(n_feat, n_state)
... self.n_feat = n_feat
... self.models = []
... self.optimizers = []
... self.criterion = torch.nn.MSELoss()
... for _ in range(n_action):
... model = torch.nn.Linear(n_feat, 1)
... self.models.append(model)
... optimizer = torch.optim.SGD(model.parameters(), lr)
... self.optimizers.append(optimizer)它接受三个参数:特征数量,n_feat;州的数量;和动作的数量。它首先为来自高斯分布的特征函数 F(s) 生成一组系数,w和b,我们将在后面定义。然后它初始化n_action线性模型,其中每个模型对应一个动作,并相应地初始化n_action优化器。对于线性模型,我们在此使用 PyTorch 的线性模块。它接受n_feat单位并生成一个输出,这是一个动作的预测状态值。随机梯度下降优化器也与每个线性模型一起初始化。每个优化器的学习率为 0.05。损失函数是均方误差。
3.我们现在继续定义get_gaussian_wb 方法,它为特征函数 F(s) 生成一组系数 w 和 b:
>>> def get_gaussian_wb(self, n_feat, n_state, sigma=.2):
... """
... 从高斯分布生成特征集的系数
... @param n_feat: 特征数量
... @param n_state: 状态数
... @param sigma: 内核参数
... @return: 特征系数
... """
... torch.manual_seed(0)
... w = torch.randn((n_state, n_feat)) * 1.0 / sigma
... b = torch.rand(n_feat) * 2.0 * math.pi
... return w, b系数w是一个矩阵,其值是n_feat根据n_state参数 sigma 定义的高斯方差分布生成的;偏差 b 是n_feat从 [0, 2π] 的均匀分布生成的值列表。
请注意,设置特定的随机种子 ( torch.manual_seed(0)) 非常重要,这样一个状态在不同的运行中始终可以映射到相同的特征。
4.w接下来,我们基于和开发将状态空间映射到特征空间的函数b:
>>> def get_feature(self, s):
... """
... 根据输入状态生成特征
... @param s: 输入状态
... @return: 特征
... """
... features = (2.0 / self.n_feat) ** .5 * torch.cos(
torch.matmul(torch.tensor(s).float(), self.w)
+ self.b)
... return features状态 s 的特征生成如下:
![]()
使用余弦变换来确保特征在 [-1, 1] 的范围内,而不管输入状态的值如何。
5.由于我们已经定义了模型和特征生成,我们现在开发训练方法,用数据点更新线性模型:
>>> def update(self, s, a, y):
... """
... 用给定的训练样本更新线性估计器的权重
... @param s: 状态
... @param a: 动作
... @param y: 目标值
... """
... features = Variable(self.get_feature(s))
... y_pred = self.models[a](features)
... loss = self.criterion(y_pred,
Variable(torch.Tensor([y])))
... self.optimizers[a].zero_grad()
... loss.backward()
... self.optimizers[a].step()给定一个训练数据点,它首先使用该get_feature方法将状态转换为特征空间。然后将生成的特征输入到给定动作的当前线性模型中a。预测结果连同目标值一起用于计算损失和梯度。然后通过反向传播更新权重 θ。
6.下一个操作涉及使用当前模型在给定状态的情况下预测每个动作的状态值:
>>> def predict(self, s):
... """
... 使用学习模型计算状态的 Q 值
... @param s: 输入状态
... @return: 状态的 Q 值state
... """
... features = self.get_feature(s)
... with torch.no_grad():
... return torch.tensor([model(features)
for model in self.models])这就是Estimator 课堂的全部内容。
7.现在,让我们尝试一些虚拟数据。首先,创建一个Estimator将 2 维状态映射到 10 维特征的对象,并使用 1 个可能的操作:
>>> estimator = Estimator(10, 2, 1)8.现在,从状态 [0.5, 0.1] 生成特征:
>>> s1 = [0.5, 0.1]
>>> print(estimator.get_feature(s1))
tensor([ 0.3163, -0.4467, -0.0450, -0.1490, 0.2393, -0.4181, -0.4426, 0.3074,
-0.4451, 0.1808])如您所见,生成的特征是一个 10 维向量。
9.在状态列表和目标状态值上训练估计器(在这个例子中我们只有一个动作):
>>> s_list = [[1, 2], [2, 2], [3, 4], [2, 3], [2, 1]]
>>> target_list = [1, 1.5, 2, 2, 1.5]
>>> for s, target in zip(s_list, target_list):
... feature = estimator.get_feature(s)
... estimator.update(s, 0, target)10.最后,我们使用经过训练的线性模型来预测新状态的值:
>>> print(estimator.predict([0.5, 0.1]))
tensor([0.6172])
>>> print(estimator.predict([2, 3]))
tensor([0.8733])具有动作的状态 [0.5, 0.1] 的预测值为 0.5847,而对于 [2, 3],它为 0.7969。
这个怎么运作...
与 TD 方法中使用 Q 表计算精确值相比,FA 方法使用更紧凑的模型来近似状态值。FA 首先将状态空间映射到特征空间,然后使用回归模型估计 Q 值。这样,学习过程就变成了有监督的。类型回归模型包括线性模型和神经网络。在这个秘籍中,我们开发了一个基于线性回归的估计器。它根据从高斯分布采样的系数生成特征。它通过梯度下降更新给定训练数据的线性模型的权重,并预测给定状态的 Q 值。
FA 大大减少了要学习的状态数量,而在 TD 方法中学习数百万个状态是不可行的。更重要的是,它能够泛化到看不见的状态,因为状态值由给定输入状态的估计函数参数化。
也可以看看
如果您不熟悉线性回归或梯度下降,请查看以下资料:
- https://towardsdatascience.com/step-by-step-tutorial-on-linear-regression-with-stochastic-gradient-descent-1d35b088a843
- https://machinelearningmastery.com/simple-linear-regression-tutorial-for-machine-learning/
使用线性函数逼近开发 Q 学习
在前面的秘籍中,我们开发了一个基于线性回归的价值估计器。作为我们 FA 之旅的一部分,我们将在 Q-learning 中使用估算器。
正如我们所见,Q 学习是一种离策略学习算法,它根据以下等式更新 Q 函数:
![]()
这里,s'是在状态s中采取行动后的结果状态a;r是相关奖励;α 是学习率;γ 是贴现因子。此外,![]() 意味着行为策略是贪婪的,其中选择状态s'中最高 Q 值的行为策略来生成学习数据。在 Q-learning 中,动作是基于 epsilon-greedy policy 采取的。类似地,Q-learning with FA 有以下误差项:
意味着行为策略是贪婪的,其中选择状态s'中最高 Q 值的行为策略来生成学习数据。在 Q-learning 中,动作是基于 epsilon-greedy policy 采取的。类似地,Q-learning with FA 有以下误差项:
![]()
我们的学习目标是将误差项最小化为零,这意味着估计的 V(st) 应满足以下等式:
![]()
现在,目标变成了找到最佳权重 θ,如 V(s)=θF(s) 中那样,以便为每个可能的动作最好地近似状态值函数 V(s)。我们在这种情况下试图最小化的损失函数类似于回归问题中的损失函数,它是实际值和估计值之间的均方误差。
怎么做...
让我们使用线性估计器开发带有 FA 的 Q 学习,Estimator,来自linear_estimator.py我们在之前的秘籍中开发的,使用梯度下降近似估计 Q 函数:
1.导入必要的模块并创建 Mountain Car 环境:
>>> import gym
>>> import torch
>>> from linear_estimator import Estimator
>>> env = gym.envs.make(“MountainCar-v0”)2.然后,开始定义 epsilon-greedy 策略:
>>> def gen_epsilon_greedy_policy(estimator, epsilon, n_action):
... def policy_function(state):
... probs = torch.ones(n_action) * epsilon / n_action
... q_values = estimator.predict(state)
... best_action = torch.argmax(q_values).item()
... probs[best_action] += 1.0 - epsilon
... action = torch.multinomial(probs, 1).item()
... return action
... return policy_function这需要一个参数 ε,其值从 0 到 1,|A|,可能的动作数量,以及用于预测状态动作值的估计器。每个动作都以 ε/ |A| 的概率采取,并以 1- ε + ε/ |A| 的概率选择具有最高预测状态-动作值的动作。
3.现在,定义使用 FA 执行 Q 学习的函数:
>>> def q_learning(env, estimator, n_episode, gamma=1.0,
epsilon=0.1, epsilon_decay=.99):
... """
... 使用函数逼近的Q学习算法
... @param env: Gym环境
... @param estimator:估计器对象
... @param n_episode:剧集数
... @param gamma:折扣因子
... @param epsilon:epsilon_greedy的参数
... @param epsilon_decay:epsilon递减因子
... """
... for episode in range(n_episode):
... policy = gen_epsilon_greedy_policy(estimator,
epsilon * epsilon_decay ** episode, n_action)
... state = env.reset()
... is_done = False
... while not is_done:
... action = policy(state)
... next_state, reward, is_done, _ = env.step(action)
... q_values_next = estimator.predict(next_state)
... td_target = reward +
gamma * torch.max(q_values_next)
... estimator.update(state, action, td_target)
... total_reward_episode[episode] += reward
...
... if is_done:
... break
... state = next_state该函数执行以下任务: q_learning()
- 在每一集中,创建一个 epsilon 因子衰减到 99% 的 epsilon-greedy 策略(例如,如果第一集中的 epsilon 为 0.1,则第二集中将为 0.099)。
- 运行一个 episode:在每个步骤中,根据 epsilon-greedy 策略采取一个动作a;使用当前估计器计算新状态的Q值;然后,计算目标值
 ,并用它来训练估计器。
,并用它来训练估计器。 - 运行n_episode 剧集并记录每个剧集的总奖励。
4.我们将特征数指定为200,学习率指定为0.03,并相应地创建一个估计器:
>>> n_state = env.observation_space.shape[0]
>>> n_action = env.action_space.n
>>> n_feature = 200
>>> lr = 0.03
>>> estimator = Estimator(n_feature, n_state, n_action, lr)5.我们使用 FA 执行 Q-learning 300 集,并跟踪每集的总奖励:
>>> n_episode = 300
>>> total_reward_episode = [0] * n_episode
>>> q_learning(env, estimator, n_episode, epsilon=0.1)6.然后,我们显示情节长度随时间的变化:
>>> import matplotlib.pyplot as plt
>>> plt.plot(total_reward_episode)
>>> plt.title('Episode reward over time')
>>> plt.xlabel('Episode')
>>> plt.ylabel('Total reward')
>>> plt.show()这个怎么运作...
如您所见,在使用 FA 的 Q 学习中,它尝试学习近似模型的最佳权重,以便最好地估计 Q 值。它类似于 TD Q-learning,因为它们都从另一个策略生成学习数据。它更适合状态空间较大的环境,因为 Q 值由一组回归模型和潜在特征近似,而 TD Q-learning 需要精确的表查找来更新 Q 值。事实上,Q-learning with FA 在每一步后都会更新回归模型,这也使得它类似于 TD Q-learning 方法。
Q-learning 模型训练完成后,我们只需要使用回归模型来预测所有可能动作的状态-动作值,并在给定状态下选择具有最大值的动作。在第 6 步中,我们导入 pyplot以绘制所有奖励,这将产生以下图:

您可以看到,在大多数情节中,在前 25 次迭代之后,汽车会在大约 130 到 160 步后到达山顶。
使用线性函数逼近开发 SARSA
我们刚刚使用上一节中的离策略 Q 学习算法解决了 Mountain Car 问题。现在,我们将使用 on-policy State-Action-Reward-State-Action ( SARSA ) 算法(当然是 FA 版本)来做到这一点。
一般而言,SARSA 算法根据以下等式更新 Q 函数:
![]()
这里,s'是在状态s中采取行动a后的结果状态;r是相关奖励;α 是学习率;γ 是贴现因子。我们也遵循 epsilon-greedy 策略来更新Q值,从而简单地选择下一个动作 a'。下一步将采取行动a' 。因此,带有 FA 的 SARSA 有以下误差项:
![]()
我们的学习目标是将误差项最小化为零,这意味着估计的 V(st) 应满足以下等式:
![]()
现在,目标变成了找到最佳权重 θ,如 V(s)=θF(s) 中那样,以便为每个可能的动作最好地近似状态值函数 V(s)。我们在这种情况下试图最小化的损失函数类似于回归问题中的损失函数,它是实际值和估计值之间的均方误差。
怎么做...
让我们使用线性估计器开发带有 FA 的 SARSA,Estimator,来自linear_estimator.py我们在配方中开发的,使用梯度下降近似估计 Q 函数:
1.导入必要的模块并创建 Mountain Car 环境:
>>> import gym
>>> import torch
>>> from linear_estimator import Estimator
>>> env = gym.envs.make(“MountainCar-v0”)2.我们将重用在之前的秘籍中开发的 epsilon-greedy 策略函数,使用线性函数逼近开发 Q-learning。
3.现在,定义执行带 FA 的 SARSA 算法的函数:
>>> def sarsa(env, estimator, n_episode, gamma=1.0,
epsilon=0.1, epsilon_decay=.99):
... """
... 使用函数逼近的 SARSA 算法
... @param env: 健身房环境
... @param estimator:估计器对象
... @param n_episode:剧集数
... @param gamma:折扣因子
... @param epsilon:epsilon_greedy 的参数
... @param epsilon_decay:epsilon 递减因子
... """
... for episode in range(n_episode):
... policy = gen_epsilon_greedy_policy(estimator,
epsilon * epsilon_decay ** episode,
env.action_space.n)
... state = env.reset()
... action = policy(state)
... is_done = False
...
... while not is_done:
... next_state, reward, done, _ = env.step(action)
... q_values_next = estimator.predict(next_state)
... next_action = policy(next_state)
... td_target = reward +
gamma * q_values_next[next_action]
... estimator.update(state, action, td_target)
... total_reward_episode[episode] += reward
...
... if done:
... break
... state = next_state
... action = next_action该sarsa()函数执行以下任务:
- 在每一集中,创建一个 epsilon 因子衰减到 99% 的 epsilon-greedy 策略。
- 运行一个 episode:在每个步骤中,根据 epsilon-greedy 策略采取一个动作a;在新状态下,根据 epsilon-greedy 策略选择新动作;然后,使用当前估计器计算新状态的 Q 值;计算目标值
 ,并使用它来更新估计量。
,并使用它来更新估计量。 - 运行n_episode 剧集并记录每个剧集的总奖励。
4.我们指定特征数为 200,学习率为 0.03,并相应地创建一个估计器:
>>> n_state = env.observation_space.shape[0]
>>> n_action = env.action_space.n
>>> n_feature = 200
>>> lr = 0.03
>>> estimator = Estimator(n_feature, n_state, n_action, lr)5.然后,我们使用 FA 执行 SARSA 300 集,并跟踪每集的总奖励:
>>> n_episode = 300
>>> total_reward_episode = [0] * n_episode
>>> sarsa(env, estimator, n_episode, epsilon=0.1)6.然后,我们显示情节长度随时间的变化:
这个怎么运作...
具有 FA 的 SARSA 尝试学习近似模型的最佳权重,以便最好地估计 Q 值。它通过采取在同一策略下选择的动作来优化估计,而不是从 Q-learning 中的另一个策略中学习经验。
同样,在训练好 SARSA 模型后,我们只需要使用回归模型来预测所有可能动作的状态动作值,并在给定状态下选择具有最大值的动作。
在第 6 步中,我们用 绘制奖励,这将导致以下图: pyplot

你可以看到,在大多数剧集中,在前 100 集之后,汽车会在大约 130 到 160 步后到达山顶。
使用经验回放合并批处理
在前两个秘籍中,我们开发了两种 FA 学习算法:分别是离策略和在策略。在这个秘籍中,我们将通过结合经验回放来提高离策略 Q-learning 的性能。
经验回放意味着我们在一个情节中存储代理的经验,而不是运行 Q-learning。有经验回放的学习阶段变成两个阶段:获取经验和更新模型基于在一个情节结束后获得的经验。具体来说,经验(也称为缓冲区,或记忆)包括过去的状态、采取的行动、收到的奖励,以及情节中各个步骤的下一个状态。
在学习阶段,从经验中随机抽取一定数量的数据点,用于训练学习模型。经验回放可以通过提供一组低相关性的样本来稳定训练,从而提高学习效率。
怎么做...
让我们使用线性估计器将经验回放应用到 FA Q 学习Estimator,来自linear_estimator.py我们在之前的秘籍中开发的线性估计,使用梯度下降近似估计 Q 函数:
1.导入必要的模块并创建 Mountain Car 环境:
>>> import gym
>>> import torch
>>> from linear_estimator import Estimator
>>> from collections import deque
>>> import random
>>> env = gym.envs.make("MountainCar-v0")2.我们将重用之前开发的 epsilon-greedy 策略函数,使用线性函数逼近配方开发 Q-learning。
3.然后,将特征数指定为200,将学习率指定为0.03,并相应地创建一个估计器:
>>> n_state = env.observation_space.shape[0]
>>> n_action = env.action_space.n
>>> n_feature = 200
>>> lr = 0.03
>>> estimator = Estimator(n_feature, n_state, n_action, lr)4.接下来,定义保存体验的缓冲区:
>>> memory = deque(maxlen=400)新的样本会被追加到队列中,只要队列中的样本超过400个,旧的样本就会被移除。
5.现在,定义执行带经验回放的 FA Q 学习的函数:
>>> def q_learning(env, estimator, n_episode, replay_size,
gamma=1.0, epsilon=0.1, epsilon_decay=.99):
... """
... Q-Learning algorithm using Function Approximation,
with experience replay
... @param env: Gym 环境
... @param estimator: 估计器对象
... @param replay_size: 我们每次用来更新模型的样本数
... @param n_episode: 剧集数
... @param gamma: 折扣因子
... @param epsilon: epsilon_greedy 的参数
... @param epsilon_decay: 递减因子
... """
... for episode in range(n_episode):
... policy = gen_epsilon_greedy_policy(estimator,
epsilon * epsilon_decay ** episode,
n_action)
... state = env.reset()
... is_done = False
... while not is_done:
... action = policy(state)
... next_state, reward, is_done, _ = env.step(action)
... total_reward_episode[episode] += reward
... if is_done:
... break
...
... q_values_next = estimator.predict(next_state)
... td_target = reward +
gamma * torch.max(q_values_next)
... memory.append((state, action, td_target))
... state = next_state
...
... replay_data = random.sample(memory,
min(replay_size, len(memory)))
... for state, action, td_target in replay_data:
... estimator.update(state, action, td_target)该函数执行以下任务:
- 在每一集中,创建一个 epsilon 因子衰减到 99% 的 epsilon-greedy 策略(例如,如果第一集中的 epsilon 为 0.1,则第二集中将为 0.099)。
- 运行一个 episode:在每个步骤中,根据 epsilon-greedy 策略采取一个动作a;使用当前估计器计算新状态的Q值;然后,计算目标值
 ,并将状态、动作和目标值元组存储在缓冲存储器中。
,并将状态、动作和目标值元组存储在缓冲存储器中。
- 在每一集之后,从缓冲存储器中随机选择replay_size样本并使用它们来训练估计器。
- 运行n_episode剧集并记录每个剧集的总奖励。
6.我们通过 1,000 集的经验回放执行 Q 学习:
>>> n_episode = 1000我们需要更多的 episode 仅仅是因为模型没有经过充分的训练,所以代理在早期的 episode 中采取随机步骤。
我们将 190 设置为重放样本大小:
>>> replay_size = 190我们还跟踪每一集的总奖励:
>>> total_reward_episode = [0] * n_episode
>>> q_learning(env, estimator, n_episode, replay_size, epsilon=0.1)7.现在,我们显示情节长度随时间的变化:
>>> import matplotlib.pyplot as plt
>>> plt.plot(total_reward_episode)
>>> plt.title('Episode reward over time')
>>> plt.xlabel('Episode')
>>> plt.ylabel('Total reward')
>>> plt.show()这将导致以下情节:

你可以看到 Q-learning with experience replay 的性能变得更加稳定。前 500 集之后的大多数集数的奖励保持在 -160 到 -120 的范围内。
这个怎么运作...
在这个秘籍中,我们借助 FA Q-learning 以及经验回放解决了 Mountain Car 问题。它优于纯 FA Q 学习,因为我们通过经验回放收集了较少校正的训练数据。我们不是急于训练估计器,而是首先将我们在事件中观察到的数据点存储在缓冲区中,然后我们从缓冲区中随机选择一批样本并训练估计器。这形成了一个输入数据集,其中样本彼此更加独立,从而使训练更加稳定和高效。
使用神经网络函数逼近开发 Q-learning
正如我们之前提到的,我们也可以使用神经网络作为逼近函数。在这个秘籍中,我们将使用 Q-learning 和神经网络进行逼近来解决 Mountain Car 环境。
FA 的目标是使用一组特征通过回归模型估计 Q 值。使用神经网络作为估计模型,我们通过增加灵活性(神经网络中的多层)和隐藏层中非线性激活引入的非线性来提高回归能力。Q-learning 模型的其余部分与具有线性近似的模型非常相似。我们还使用梯度下降来训练网络。学习的最终目标是为每个可能的动作找到网络的最佳权重,以最好地近似状态值函数 V(s)。我们试图最小化的损失函数也是实际值和估计值之间的均方误差。
怎么做...
让我们从实现基于神经网络的估计器开始。我们将重用我们在使用梯度下降近似估计 Q 函数一节中开发的线性估计器的大部分。不同之处在于,我们使用隐藏层连接输入层和输出层,然后是激活函数,在本例中是 ReLU(整流线性单元)函数。所以,我们只需要修改__init__方法如下:
>>> class Estimator():
... def __init__(self, n_feat, n_state, n_action, lr=0.05):
... self.w, self.b = self.get_gaussian_wb(n_feat, n_state)
... self.n_feat = n_feat
... self.models = []
... self.optimizers = []
... self.criterion = torch.nn.MSELoss()
... for _ in range(n_action):
... model = torch.nn.Sequential(
... torch.nn.Linear(n_feat, n_hidden),
... torch.nn.ReLU(),
... torch.nn.Linear(n_hidden, 1)
... )
... self.models.append(model)
... optimizer = torch.optim.Adam(model.parameters(), lr)
... self.optimizers.append(optimizer)如您所见,隐藏层有n_hidden节点,ReLU 激活 ,torch.nn.ReLU()位于隐藏层之后,紧接着是产生估计值的输出层。
神经网络的其他部分Estimator与线性相同Estimator。您可以将它们复制到文件 nn_estimator.py中。
现在,我们继续使用具有经验回放的神经网络进行 Q 学习,如下所示:
1.Estimator从我们刚刚开发的 导入必要的模块,包括神经网络估计器 ,nn_estimator.py并创建 Mountain Car 环境:
>>> import gym
>>> import torch
>>> from nn_estimator import Estimator
>>> from collections import deque
>>> import random
>>> env = gym.envs.make("MountainCar-v0")2.我们将重用在使用线性函数逼近开发 Q 学习一节中开发的 epsilon-greedy 策略函数。
3.然后我们指定特征数为 200,学习率为 0.001,隐藏层的大小为 50,并相应地创建一个估计器:
>>> n_state = env.observation_space.shape[0]
>>> n_action = env.action_space.n
>>> n_feature = 200
>>> n_hidden = 50
>>> lr = 0.001
>>> estimator = Estimator(n_feature, n_state, n_action, n_hidden, lr)4.接下来,定义保存体验的缓冲区:
>>> memory = deque(maxlen=300)新的样本会被追加到队列中,只要队列中的样本超过 300 个,旧的样本就会被移除。
5.我们将重用q_learning 我们在之前的秘籍中开发的功能,使用经验回放合并批处理。它通过经验回放执行 FA Q 学习。
6.我们使用 1,000 集的经验回放执行 Q 学习,并将 200 设置为回放样本大小。
>>> n_episode = 1000
>>> replay_size = 200我们还跟踪每一集的总奖励:
>>> total_reward_episode = [0] * n_episode
>>> q_learning(env, estimator, n_episode, replay_size, epsilon=0.1)7.然后,我们显示情节长度随时间的变化:
>>> import matplotlib.pyplot as plt
>>> plt.plot(total_reward_episode)
>>> plt.title('Episode reward over time')
>>> plt.xlabel('Episode')
>>> plt.ylabel('Total reward')
>>> plt.show()这个怎么运作...
使用神经网络的 FA 与线性函数逼近非常相似。它不是使用简单的线性函数,而是使用神经网络将特征映射到目标值。该算法的其余部分基本相同,但由于神经网络和非线性激活的结构更复杂,因此具有更高的灵活性,因此具有更强的预测能力。
在第 7 步中,我们绘制了随时间变化的情节长度,这将导致以下情节:
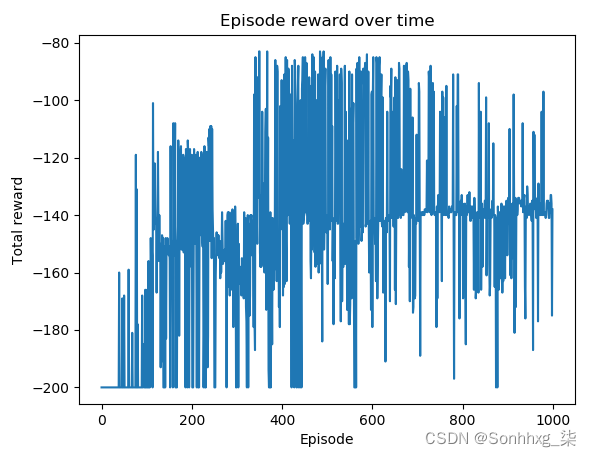
您可以看到使用神经网络进行 Q-learning 的性能优于使用线性函数。前 500 集之后的大多数集数的奖励保持在 -140 到 -85 的范围内。
也可以看看
如果您想温习一下神经网络知识,请查看以下资料:
- Neural Networks — PyTorch Tutorials 1.13.0+cu117 documentation
- https://www.cs.toronto.edu/~jlucas/teaching/csc411/lectures/tut5_handout.pdf
用函数逼近解决 CartPole 问题
这是本章的额外秘诀,我们将在其中使用 FA 解决 CartPole 问题。
正如我们在第 1 章,强化学习和 PyTorch 入门中看到的,我们在模拟 CartPole 环境食谱中模拟了 CartPole 环境,并分别使用随机搜索、爬山算法和策略梯度算法解决了环境,在食谱中包括实施和评估随机搜索策略,开发爬山算法,以及开发策略梯度算法。现在,让我们尝试使用我们在本章中讨论的内容来解决 CartPole。
怎么做...
我们演示了基于神经网络的 FA 的解决方案,无需经验回放,如下所示:
1.导入必要的模块,包括神经网络,我们在上一节开发 Q-learning with neural net function approximationEstimator中从nn_estimator.py中开发,并创建一个 CartPole 环境:
>>> import gym
>>> import torch
>>> from nn_estimator import Estimator
>>> env = gym.envs.make("CartPole-v0")2.我们将重用在之前的秘籍中开发的 epsilon-greedy 策略函数,使用线性函数逼近开发 Q-learning。
3.然后我们指定特征数为 400(注意 CartPole 环境的状态空间是 4 维),学习率为 0.01,隐藏层的大小为 100,并相应地创建一个神经网络估计器:
>>> n_state = env.observation_space.shape[0]
>>> n_action = env.action_space.n
>>> n_feature = 400
>>> n_hidden = 100
>>> lr = 0.01
>>> estimator = Estimator(n_feature, n_state, n_action, n_hidden, lr)4.我们将重用q_learning我们在之前的秘籍中开发的函数,使用线性函数逼近开发 Q-learning。这执行 FA Q 学习。
5.我们使用 FA 对 1,000 集进行 Q 学习,并跟踪每集的总奖励:
>>> n_episode = 1000
>>> total_reward_episode = [0] * n_episode
>>> q_learning(env, estimator, n_episode, epsilon=0.1)6.最后,我们显示剧集长度随时间变化的图:
>>> import matplotlib.pyplot as plt
>>> plt.plot(total_reward_episode)
>>> plt.title('Episode reward over time')
>>> plt.xlabel('Episode')
>>> plt.ylabel('Total reward')
>>> plt.show()这个怎么运作...
在这个秘籍中,我们使用带有神经网络的 FA 算法解决了 CartPole 问题。请注意,环境有一个四维观察空间,是 Mountain Car 的两倍,因此我们直观地加倍了我们使用的特征数量,并相应地增加了隐藏层的大小。随意尝试使用带有神经网络的 SARSA,或带有经验回放的 Q-learning,看看它们中的哪一个表现更好。
在第 6 步中,我们绘制了随时间变化的剧集长度,这将导致以下情节:
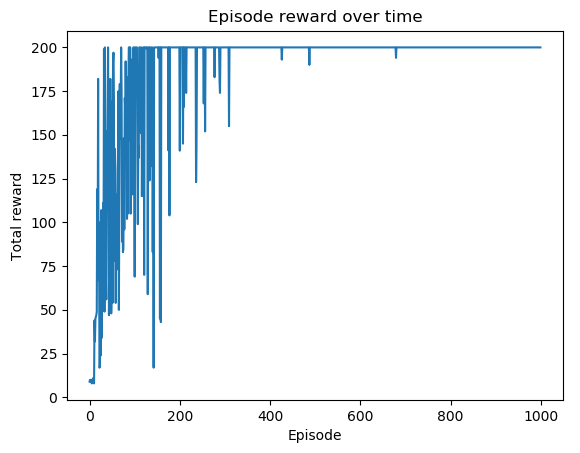
可以看到前300集之后的大部分集数的总奖励都是最大值+200。