提示：数字滤波算法 在数字信号处理应用中使用微控制器

---

1.介绍

数字信号处理算法是功能强大的工具，可为常见问题提供算法解决方案。例如，数字滤波器相对于模拟滤波器具有许多优势。传统上，这些算法是使用专用数字信号处理（DSP）芯片，FPGA或RISC处理器实现的。尽管这些解决方案在其目的上非常有效，但它们仅在系统中执行一项功能，并且既昂贵又庞大。本应用笔记讨论了一种使用Silicon Labs微控制器的替代解决方案，该解决方案可在较小的空间内实现DSP算法，同时仍具有可用于其他任务的大量CPU带宽。

本应用笔记讨论了C8051F12x和C8051F36x系列微控制器上三种DSP解决方案的实现：

• FIR滤波器
• 用于DTMF解码的Goertzel算法
• FFT算法

对于这些主题中的每一个，我们都会介绍算法，并使用乘法和累加（MAC）引擎讨论这些算法在具有DSP功能的MCU上的实现，并提供CPU带宽和内存使用情况的列表。

---

提示：以下是本篇文章正文内容，下面案例可供参考

1.1. 关键点

100个峰值MIPS CPU，2周期16x16 MAC引擎以及片上ADC和DAC使C8051F12x和C8051F36x非常适合DSP应用。在5x5毫米的C8051F36x微控制器上使用这些资源
8位MCU可以实时处理FIR滤波器的数据和用于DTMF解码的Goertzel算法，并实现完整的FFT。

2. 数字FIR滤波器

2.1. 数字滤波器算法

数字滤波器方程式基于z域中所示的以下基本传递函数：
Y(z) = H(z)X(z),
其中Y（z）是滤波器的输出，X（z）是滤波器的输入，H（z）是滤波器的传递函数。
H（z）可以扩展如下：

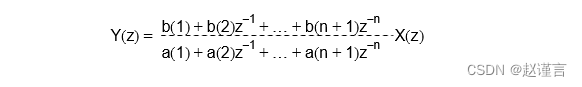
其中a和b是系数集合，z是延迟元素。

2.1.1. IIR滤波器算法

通过将展开的H（z）的分母移动到方程的左侧，IIR拓扑结构直接从该方程扩展：
(a(1)+a(2)z–1+…+a(n+1)z–n)Y(z) = (b(1)+b(2)z–1+…+b(n+1)z–n)X(z)
在时域中，此等式如下所示：
a(1)y(k) + a(2)y(k –1)+…+a(n+1)y(k –n) = b(1)x(k) + b(2)x(k –1)+…+b(n+1)x(k –n)
其中y（k）代表当前滤波器输出，x（k）代表当前输入，y（k-1）代表先前的输出，x（k-1）代表先前的输入，依此类推。如果对y（k）求解该方程式：

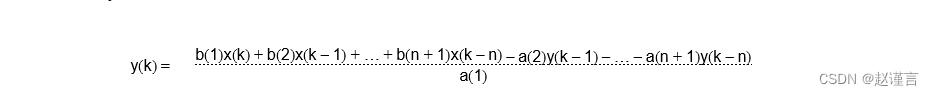
该方程式表明，IIR滤波器是一个反馈系统，它根据当前和先前的输入以及先前的输出生成电流输出。IIR结构具有独特的优点和缺点。IIR结构的主要优点是它提供的频率响应可与高阶FIR滤波器相媲美。这导致实现过滤器所需的计算量减少。IIR滤波器依赖于反馈，因此可能会出现不稳定的情况。结果，它们更难以设计，必须特别注意防止系统不稳定。IIR滤波器也可能具有非线性相位响应，这使其不适用于某些需要线性相位的应用。最后，由于它们依赖于过去的输出，因此它们倾向于对量化噪声更敏感，从而使其难以用16位定点硬件实现。通常，IIR滤波器的实现需要32位硬件。

2.1.2. FIR滤波器算法

相反，FIR滤波器没有反馈。滤波器传递函数的推导方法与以前相同。但是，系数只有一个，它等于1（a（1）= 1）。当求解y（k）的方程式时：

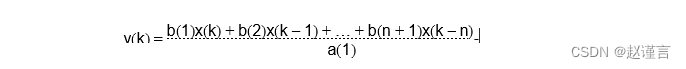
对于FIR算法，仅基于当前和先前输入生成当前输出。实际上，FIR是加权和运算。
FIR滤波器具有几个优点和缺点。主要优点之一是FIR滤波器固有地稳定。该特性使设计FIR滤波器比设计IIR滤波器容易。另外，FIR滤波器可以提供线性相位响应，这对于某些应用可能很重要。FIR滤波器的另一个重要优点是它们对系数的量化噪声具有更高的抵抗力。结果，可以很容易地使用16位定点硬件（例如C8051F12x和C8051F36x上的乘法和累加模块）来实现它们。FIR滤波器的主要缺点是，它们需要更多的数学运算才能获得类似于IIR滤波器的响应。由于设计的简便性以及它们与定点微控制器的兼容性，FIR滤波器将成为本应用笔记其余部分的实施讨论的重点。
用a（1）= 1和C代替b常数，FIR滤波器的公式如下：
y(n) = C0x(n) + C1x(n-1) + C2x(n-2) + C3x(n-3) + …,
其中y（n）是最新的滤波器输出，而x（n）是最新的滤波器输入。过滤器确实依赖先前的输入，如x（n-1），x（n-2）等项所示。Cx常数确定滤波器响应，并且可以使用许多不同的算法得出，每种算法产生不同的特性。

该算法的工作原理如下：

第一个输入x（1）乘以C0。输出y（1）如下：
y(1) = C0x(1)
然后将x（1）输入保存下来，以供下一次通过FIR算法使用。
第二个输入x（2）乘以C0，前一个输入x（1）乘以C1。输出y（2）如下：
y(2) = C0x(2) + C1x(1)
x（1）和x（2）输入保存为下一个输入x（3），依此类推。
FIR滤波器的阶数等于常数数的1以下，并且表示复杂程度和需要存储的输入样本数。阶数越高，滤波器的特性越好（非衰减区域中的陡峭曲线和平坦响应）。

2.2. C8051F12x和C8051F36x的FIR算法实现

C8051F12x和C8051F36x MAC引擎非常适合实现FIR算法。每次通过过滤器都需要相乘和累加，MAC引擎旨在快速有效地实现该累加和累加。结合100 MIPS 8051处理器，'F12x和’F36x能够实时计算FIR滤波器算法，同时仍为其他任务留出足够的CPU资源。

2.2.1. 实施优化

在FIR算法中，滤波器的先前输入用于每次输出计算。FIR算法可以使用循环缓冲区结构来处理输入样本的流，而不是通过数组将这些数据点混排以将最新输入放置在同一位置（例如地址0）。循环缓冲区使用数组和保存的索引来用最新的样本覆盖最旧的样本，并按其正确顺序处理输入。这种结构提供了一种将输入样本与其相应的滤波器系数正确匹配的方法，而不会产生过多的数据移动开销。
FIR滤波器具有令人感兴趣的系数镜像特性，可以对滤波器算法进行重大优化。生成特定滤波器的系数后，这些系数将始终围绕中心系数进行镜像。例如，在n阶滤波器中，第一个系数C0等于最后一个系数Cn，系数C1等于系数Cn-1，依此类推。此属性的好处是一半的指令用于加载可以避免进入MAC的系数。取而代之的是，可以将每个系数加载到MAC中，然后依次跟两个将与之相乘的样本。这样可将到MAC的数据移动操作减少约25％，并提供更好的过滤性能。
此外，某些滤波器具有第二个属性，其中每个其他系数的值均为零，从而可以进行更多优化。这发生在频率响应对称于奈奎斯特速率的1/2（采样速率的1/4）的半带滤波器中。不需要执行这些与零值系数相乘的运算，因为结果将仅为零，并且累加的输出将保持不变。从过滤器循环中删除这些不必要的乘法将对执行时间产生重大影响。

2.2.2. FIR滤波器示例

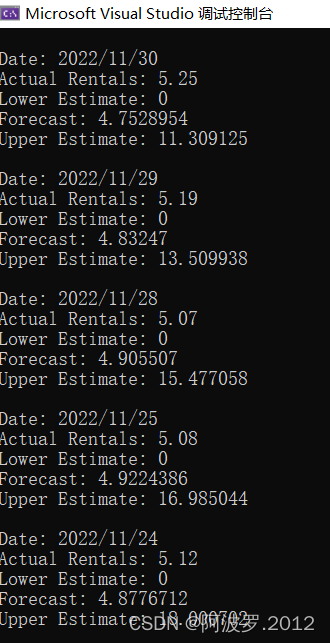
应用程序使用FIR滤波器执行任务。例如，语音应用程序可以使用低通FIR滤波器来衰减4 kHz以上的频率。为了在支持DSP的MCU上演示FIR算法，FIR_Demo.c程序在50 Hz至5 kHz之间测量滤波器的频率响应。程序记录当前频率下滤波器的输入RMS值和输出RMS值，并将该频率，输入RMS值和输出RMS值打印到UART。然后，它们会增加生成的频率并重新开始。这些程序利用IDAC生成频率扫描，并使用10 kHz的ADC采样频率。计算输入和输出的RMS值，并将其用于输出功率计算。

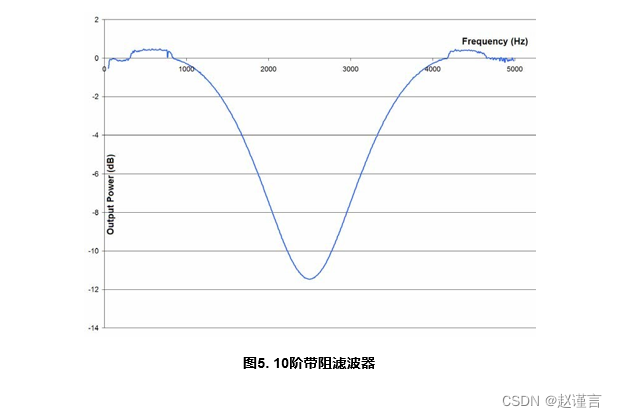
本应用笔记FIR示例代码利用了循环缓冲区和镜像优化的优势，因为它们是所有FIR滤波器的属性。Half-Band属性仅适用于某些FIR设计，因此不包括此优化。图1说明了FIR固件过程。

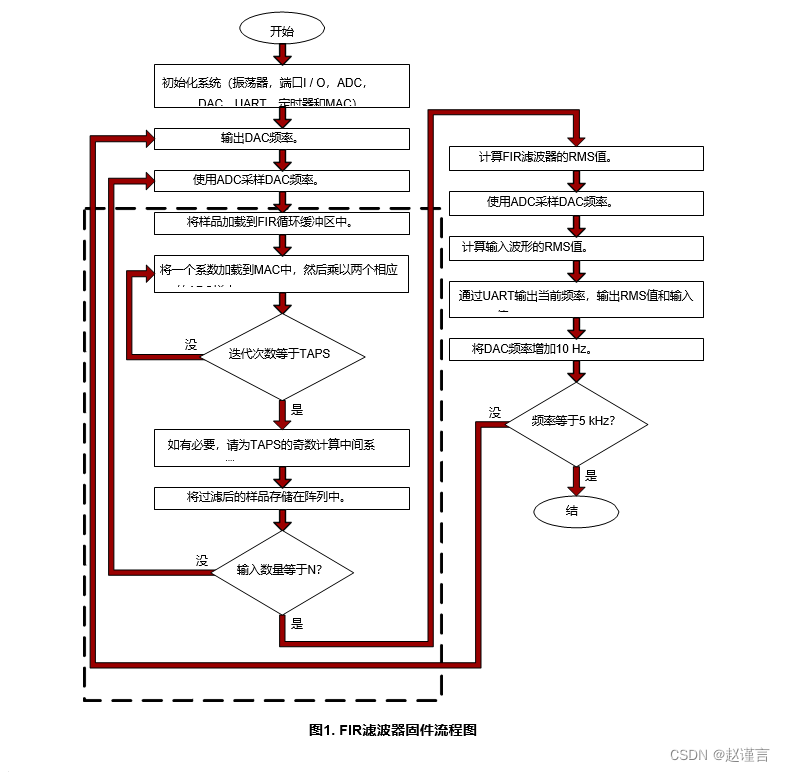
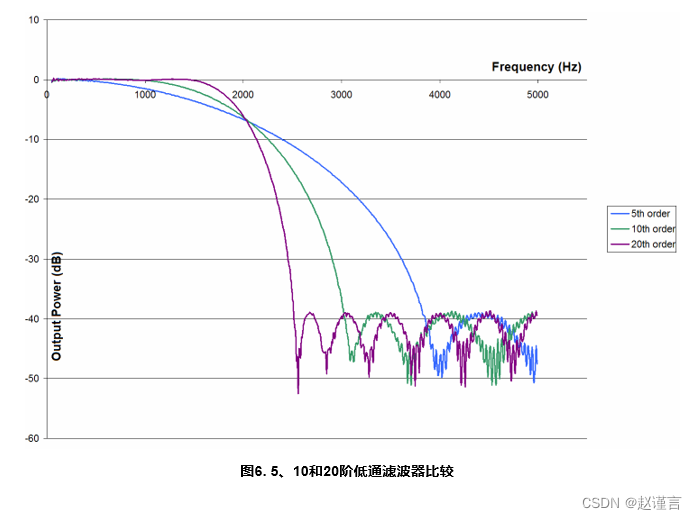
数字2 通过5 说明了使用FDATool（MATLAB）设计并在C8051F12x和C8051F36x系列设备上实现的几种不同滤波器的频率响应。在所有情况下，微控制器的滤波器响应输出均与FDATool中设计的滤波器响应相匹配。

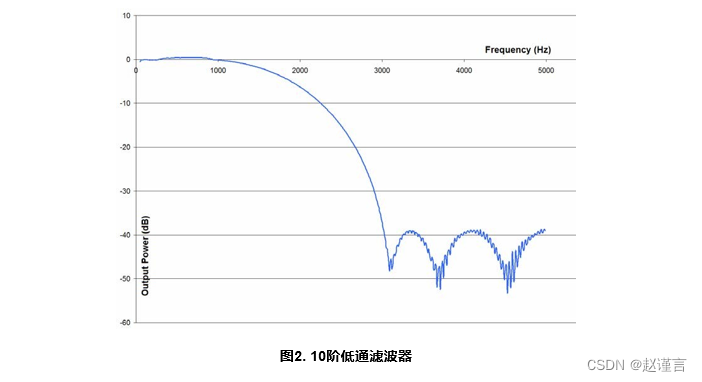
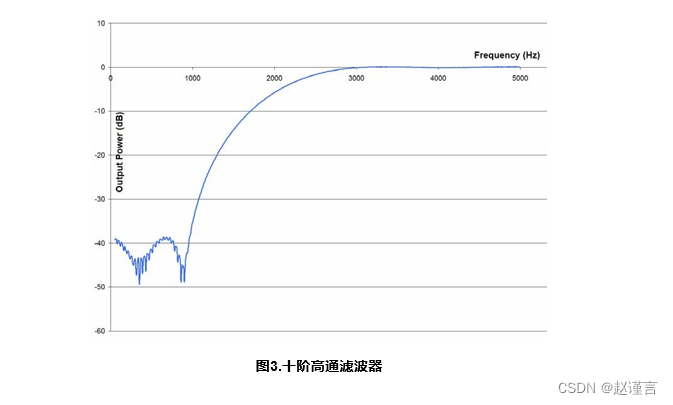
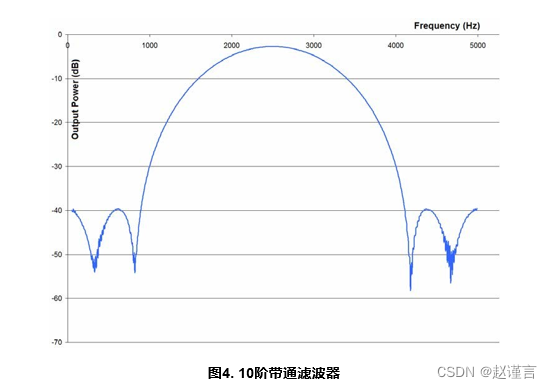
2.3. 运行FIR演示

编译FIR Demo示例代码将需要完整版本的Keil编译器（由于代码大小和sqrt（）函数）或SDCC。该固件位于Silicon Labs MCU应用程序网页上的相关应用程序说明软件包中。
有关特定于C8051F120目标板或C8051F360 ToolStick子卡的硬件设置，请参阅"5. 硬件设置”（第22页）.
要重新编译程序，请打开Silicon Laboratories IDE，然后将适当的FIR_Demo.c文件添加到项目中并进行构建。在项目工具链集成菜单下，选择编译器和可执行文件路径。该示例代码适用于C8051F120目标板或C8051F360 ToolStick子卡，尽管可以为其他平台修改程序。生成项目，连接到目标设备，然后下载代码。
使用目标板上的RS-232连接器和终端程序（例如超级终端）连接到C8051F120。使用ToolStick终端程序连接到’F360 ToolStick子卡板。将输出保存到文件中，然后使用FIR_graph.xls Excel电子表格来绘制过滤器响应的图形（可以在电子表格中找到说明）。

2.3.1. 性能

使用三个不同阶数的三个低通滤波器，以系统时钟周期和所使用的CPU带宽（ADC采样率为10 kHz）测量FIR滤波器的性能。

C8051F12x和C8051F36x系列微控制器的性能按以下三个不同的滤波器顺序如下：

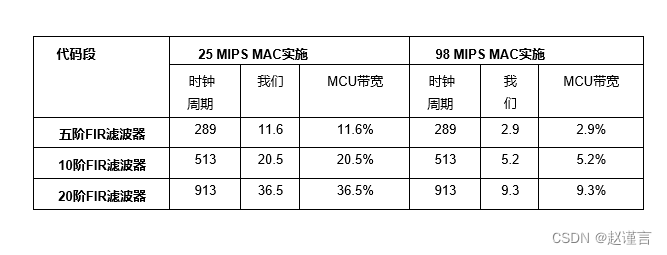
即使使用20阶滤波器，该滤波器也仅占用微控制器带宽的9.3％，从而使MCU可以完成许多其他任务，或者，如果不需要其他任务，则可以在不使用时休眠并节省功耗。

3. Goertzel算法

许多嵌入式系统都对输入波形中的一组或一组频率感兴趣。当这些感兴趣的频率已知时，Goertzel算法是一个有用的工具。
Goertzel算法是一种专用算法，旨在检测单个频率的存在。尽管推导来自单仓离散傅立叶变换输出*，但它以两极IIR滤波器的形式实现。
*注：里昂，理查德。了解数字信号处理。第二版。2004。

Goertzel方程如下：

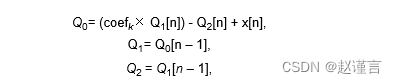
其中x [n]是当前输入，Q0是最新输出，Q1是前一次迭代的输出，而Q2是前两次迭代的输出。系数coefk取决于某些系统参数，例如目标频率和输入总数N。在特定频率下，输入波形的功率如下：

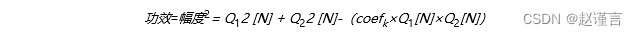
由于Goertzel方程中的离散傅立叶变换影响，该算法只有在当前输入数n等于N（即算法使用的输入总数）之前，才具有有效的输出。这意味着滤波器的输出在处理了N个输入样本之前是无效的。

3.1. 用于DTMF应用的Goertzel算法

双音多频（DTMF）使用四个频率代表四行，使用四个频率代表四列。通过覆盖行频率和列频率而创建的网格是按键式电话键盘。键盘上的每个按钮都由波形表示，该波形是行频率和列频率的组合。为行音和列音选择的音是彼此特定的非整数倍，因此一个音不容易被误认为是另一音。
DTMF的音调包含在正常语音范围内。为防止在通话过程中DTMF音调出现误报，请使用音调的二次谐波。如果输入波形包含比预期的更强的DTMF频率二次谐波，则输入波形很可能是语音而不是DTMF音调。

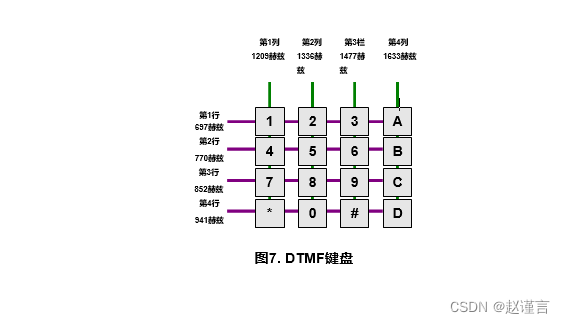
DTMF音调生成是一个容易解决的问题，可以通过逐步访问恒定的SINE表并将音调加在一起来解决。例如，“ 5”音是行2音770 Hz和列2音1336 Hz的组合，如图所示8.

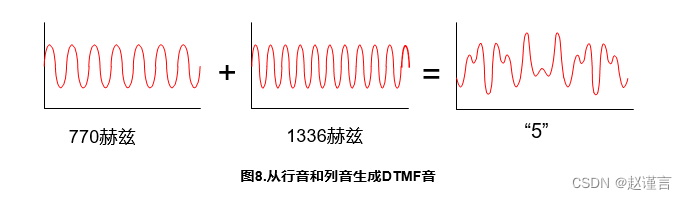
但是，DTMF检测要求系统搜索一行音和一列音的存在，并将语音与纯DTMF音区分开。由于Goertzel算法的计算速度相对较快，并且不需要存储不再活跃参与计算的过去输入，因此它是实现DTMF解码的可行解决方案。
然后，用于DTMF应用的Goertzel方程变为：

3.2. 在C8051F12x和C8051F36x上实现DTMF的Goertzel算法

MAC引擎和100 MIPS核心CPU速度使C801F12x和C8051F36x能够轻松快速地实现用于DTMF音调检测的Goertzel算法。Goertzel算法的方程式是一系列适合于MAC的乘法和加法。

3.2.1. 实施优化

将Goertzel算法用于DTMF需要16个滤波器：8个用于基本DTMF频率，8个用于DTMF频率二次谐波。但是，这两组过滤器不需要同时计算。如果将它们分为两组，则可以更早地检测到DTMF音调，并且可以在初始音调检测后检查二次谐波。另外，通过将两个过滤器分开可以大大减少存储需求，因为存储可以在两组之间重复使用。

3.2.2. Goertzel DTMF示例

DTMF_Demo.c程序使用片上DAC和恒定的SINE表生成DTMF音调。该示例代码使用ADC ISR（中断服务程序）中的Goertzel算法检测音频。DAC以100 kHz更新输出波形，而ADC以8 kHz采样输入。该程序使用UART显示键盘，并要求产生提示音。当要求发出声音时，该声音会在DAC上生成一段设定的时间，然后ADC对波形进行采样并确定是否存在DTMF声音。如果检测到提示音，则将指示符打印到UART。在应用示例代码中，将8个基本频率和8个二次谐波分成两组滤波器，以优化存储器使用。图9说明了Goertzel DTMF固件过程。

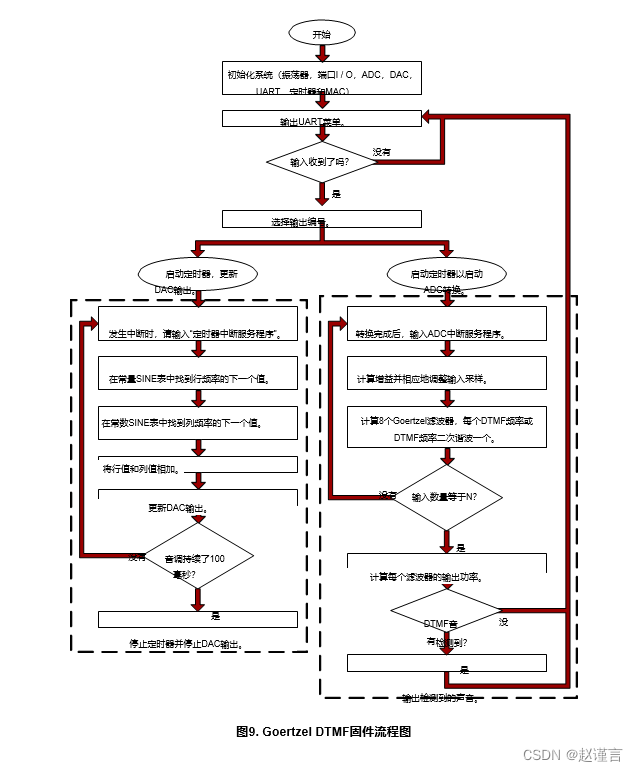
因为示例代码生成了DTMF音并在同一设备上对其进行了检测，所以系统之间存在同步，而同步通常不会出现在应用程序中。对于两个动作在单独平台上异步发生的系统，本应用笔记中还提供了单独的生成和检测代码。

3.3. 运行Goertzel DTMF演示

Goertzel DTMF演示程序需要Keil编译器的完整版本（因为代码大小大于4 kB）或SDCC。该固件位于Silicon Labs应用程序网页上的相关应用程序说明软件包中。
有关特定于C8051F120目标板或C8051F360 ToolStick子卡的硬件设置，请参阅"5. 硬件设置”（第22页）.
要重新编译该程序，请打开Silicon Laboratories IDE，然后将DTMF_Demo.c文件添加到项目中并进行构建。在项目工具链集成菜单下，选择适当的编译器和可执行文件路径。该项目可用于C8051F120目标板或C8051F360 ToolStick子卡，但可以为其他平台进行修改。生成项目，连接到目标，然后下载代码。
使用目标板上的RS-232连接器和终端程序（例如超级终端）连接到C8051F120。使用ToolStick终端程序连接到’F360 ToolStick子卡板。浏览UART菜单以生成DTMF音调。UART会在产生声音时以及在重新打印菜单之前检测到声音时输出。

3.4. 性能

MAC引擎和100 MIPS核心CPU速度允许C8051F12x和C8051F36x系列微控制器大大优于运行相同算法的25 MIPS CPU。这使得’F12x和’F36x可以在收集输入时同时并实时计算八个滤波器的算法。此外，'F12x和’F36x可以实时计算每个频率的功率。

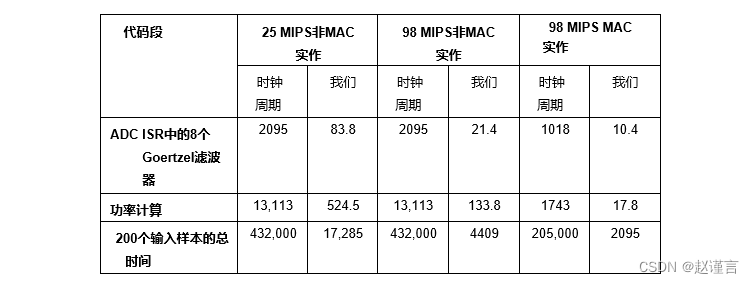
正常实现以25 MIPS运行时，功率计算必须在每个ADC输入的计算之间的背景中进行，并且由于每个采样周期的大部分时间都由计算本身占用，因此功率计算结果可能会延迟。但是，使用MAC和100 MIPS CPU带宽的’F12x和’F36x实现速度要快八倍以上，并且滤波器和功率计算可以在下一个ADC采样之前完全在ADC ISR（中断服务程序）中完成。因此，功率计算和Goertzel过滤器不需要花太多时间来完成其他任务。在25 MIPS的设备中，DTMF应用程序将占用设备的大部分带宽，但是具有DSP功能的微控制器可以轻松完成其他任务。
此外，与该算法的MAC版本相比，通常的实现方式需要更多的代码空间（5355字节的代码对5057字节的代码）和更多的RAM（165字节对126字节）来实现。

4. 快速傅立叶变换

傅立叶变换将连续的时域信号作为其输入，并计算该信号的频率含量。但是，在具有ADC输入的实际系统中，时域信号是离散的而不是连续的，因此必须使用离散傅立叶变换（DFT）。快速傅立叶变换（FFT）产生与DFT相同的输出，但效率更高。
FFT提取输入数据数组，然后将其递归分为两半，直到数据成对出现为止。然后，FFT为数据计算2点FFT，并使用输出来计算4点FFT。然后，将4点FFT的输出用于计算8点FFT，依此类推，直到完成N点FFT。
DFT需要进行N2次复杂计算才能生成输出，其中N是DFT中的点数。但是，FFT仅需要N / 2 x log2N个复数计算。随着FFT（N）输入点数量的增加，与DFT相比，FFT效率大大提高。

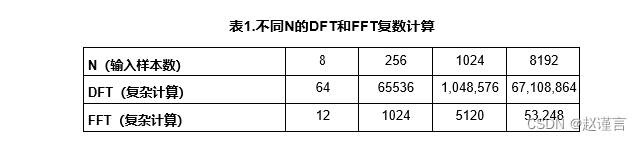
FFT允许在系统中进行频率分析，并且是任何DSP目录的主要内容。FFT通常在DSP上实现，而具有DSP功能的MCU在嵌入式系统中具有FFT功能，具有通用可编程微控制器的灵活性。

4.1. FFT算法

FFT的工作原理是获取一个N点输入数据数组，然后将其递归分为两半，直到剩下两点数据对为止。然后将这些2点对组合以创建4点结果，然后将4点对组合以创建8点结果，依此类推。结果，N必须是2的幂（2、4、8、16、32、64等）。
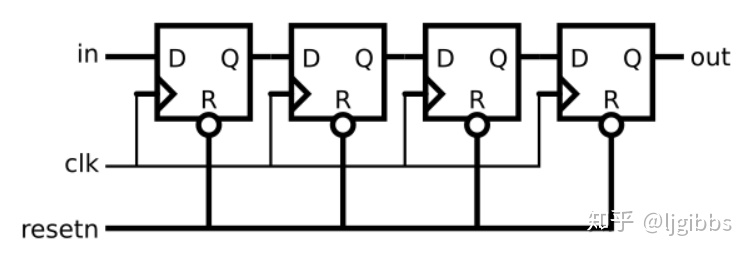
2点组合或级是FFT的基本组成部分。对于每个进行阶段都重复此算法。如图所示，计算出2点“蝴蝶”。

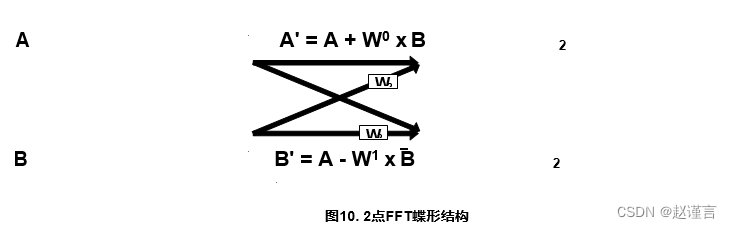
图中显示的W因子是“旋转”。旋转是基于当前阶段的点数计算的正弦/余弦因子。旋转的方程式如下：

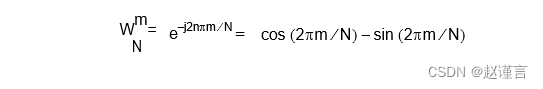
其中2点级的N是2，m是0到N-1（在这种情况下为0和1）。请注意，A和B都是复数，因此它们都包含实部和虚部。
组合两个2点蝶形以创建4点FFT。第一个2点蝶形的A和B输出变为A1和A2，第二个2点蝶形的A和B输出变为B1和B2。4点FFT如下图所示图11.

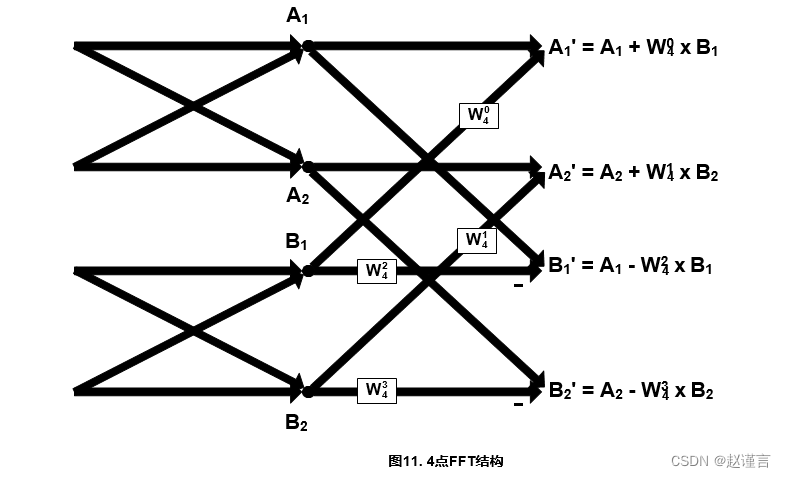
在4点FFT的情况下，W因子的m从0到3，N为4。

同样，8点FFT是两个4点FFT的组合：

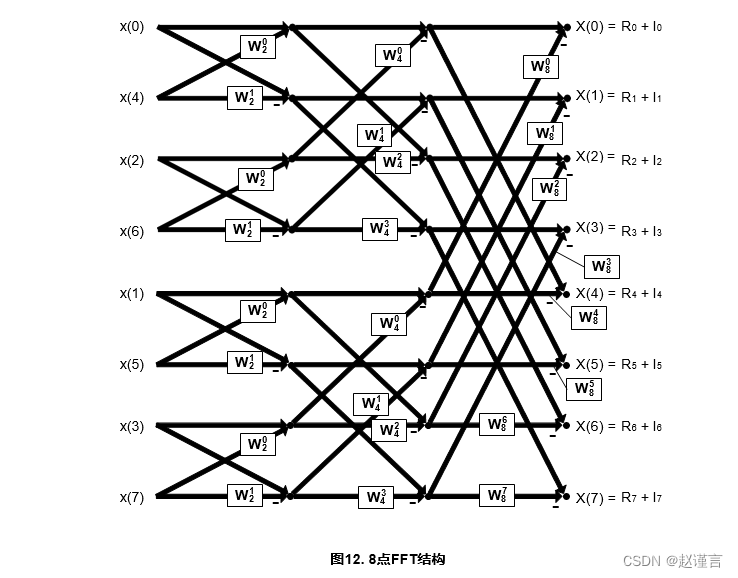
对于FFT的每个阶段，复数数据点的数量保持不变（2点阶段为32个数据点，4点阶段为32个数据点），因此FFT是一种计算量大的算法，尤其是当N变大。此外，早期的任何错误都会在后期组合，因此计算越精确，FFT算法的实现就越好。

4.1.1. 加窗

如果采样频率不是输入波形的理想倍数，则输入数据集在第一个数据点和最后一个数据点之间将不连续。这种不连续性可能导致FFT产生虚假能量。为了消除这种情况，使用了使输入波形符合特定形状的窗口。该窗口可更改波形的幅度，但不会更改频率分量。

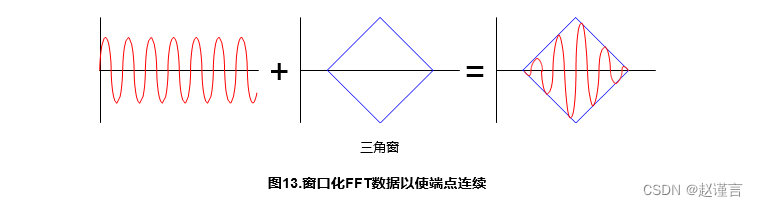
尽管Window有助于产生虚假的能量，但副作用之一是，能量倾向于在垃圾箱之间散布更多。不同的窗口函数*的主瓣宽度和旁瓣幅度不同。Windows的几个示例是Hamming，Hanning，Blackman和Triangle。
*注：里昂，理查德。了解数字信号处理。第二版。2004。

4.1.2. 位反转

在FFT算法中，不能线性访问数组形式的输入数据。2点蝶形中针对16点FFT组合的前两个值是地址0和8的数据（将数据分为两半，0和8是每半的第一个数据）。接下来的两个地址组合为4与12，然后2与10以及6与14。
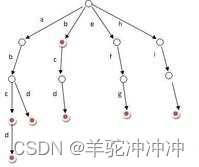
使用较小的FFT，计算每次通过的新索引非常简单。但是，FFT越复杂，计算索引所花费的时间就越多。如果以“位反转”的方式对输入数组进行重新排序，则可以绕开这些索引计算。例如，请参阅图14该图显示了具有16个输入数据点的16点FFT。

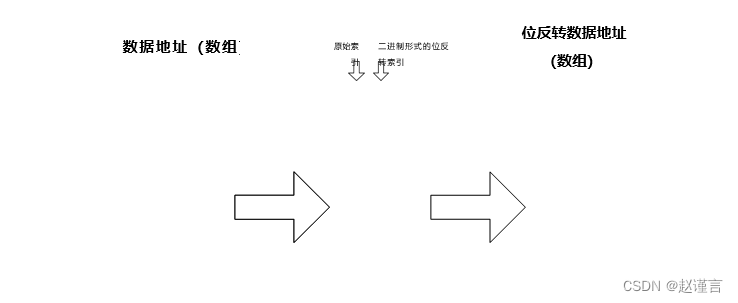
在前几个2点FFT中合并的数据对以蓝色（0和8），绿色（4和12），红色（2和10）和紫色（6和14）着色。地址的十进制值与二进制格式一起显示，以在位反转后清除地址的原始值。在位反转中，位3与位0交换，位2与位1交换，因此地址“ 1”或0001转换为地址“ 8”或1000。
现在，将索引减少为整个数组的简单线性级数。请注意，所有偶数地址都出现在数组的开头，而所有奇数地址都出现在数组的结尾。

4.1.3. 解释FFT输出

FFT输出是一系列“箱”，代表频带中的能量。每个仓表示每个周期的周期值。例如，使用以下64点FFT输出：

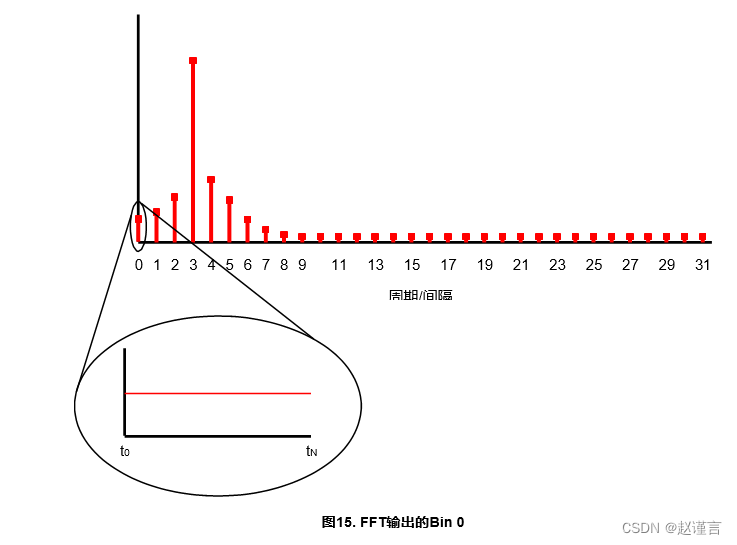
0 bin表示0个周期/间隔或一个dc值。同样，1 bin表示1个周期/间隔。

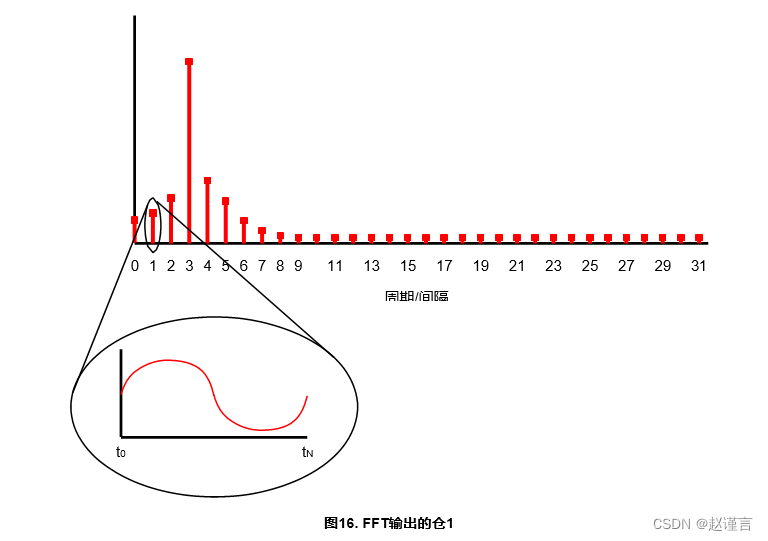
间隔是采样所表示的总时间，或N xt采样，其中t采样是采样周期。这样，每个单元代表一个频率，该频率是采样频率的一部分。可以通过以下公式将垃圾箱转换为频率：
fbin= (bin/N) xf采样

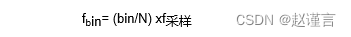
4.2. C8051F12x和C8051F36x的FFT算法实现

C8051F12x和C8051F36x带有MAC引擎和100 MIPS峰值CPU，与许多8051平台相比，可以更快地处理Windowing和FFT计算。窗口化例程包括将输入数据点乘以一组常数，使用MAC可以使其更快。FFT算法是一组也适用于MAC的加法和乘法。

4.2.1. 实施优化

在未优化的FFT中，将为每个复杂的计算计算旋转。但是，在FFT中有很多情况，正弦或余弦函数为0、1或–1。在这些情况下，通过预先优化方程式来消除旋转计算和零项，可以节省大量速度。例如，在2点FFT中，正弦项始终为零，可以从2点计算中将其删除。

4.2.2. FFT范例

示例代码使用IDAC生成波形，并使用ADC以10 kHz采样该波形的256个数据点以进行256点FFT。在对输入进行采样之后，将使用布莱克曼窗口，位反转例程和FFT算法通过Windowing例程运行数据。最终输出（实数和虚数）使用UART以及仓号的前半部分（直到1/2 f采样）显示。图17显示FFT固件程序。

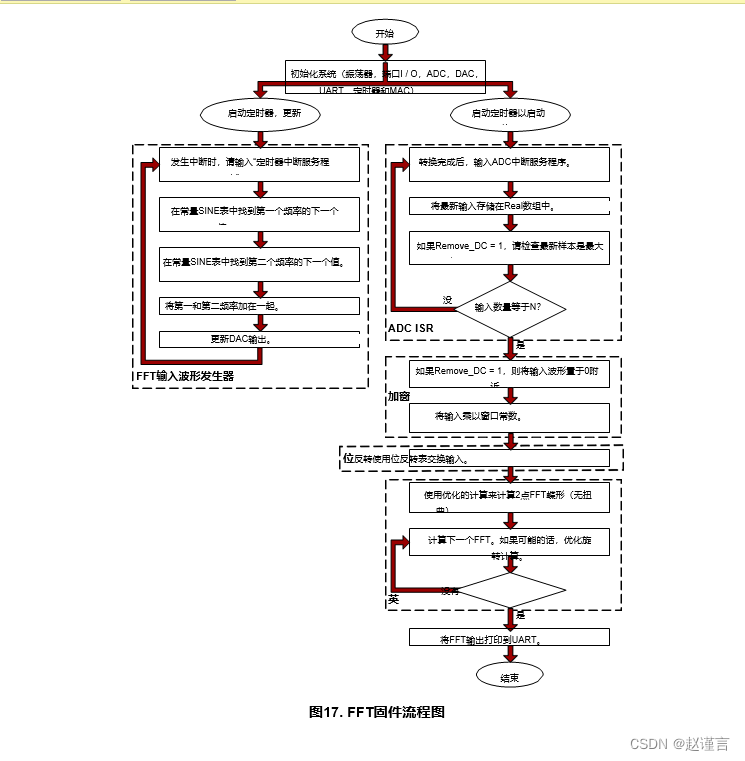
FFT_Demo.c中的采样波形是770 Hz和1336 Hz的组合。Excel的图形输出如下所示图18.

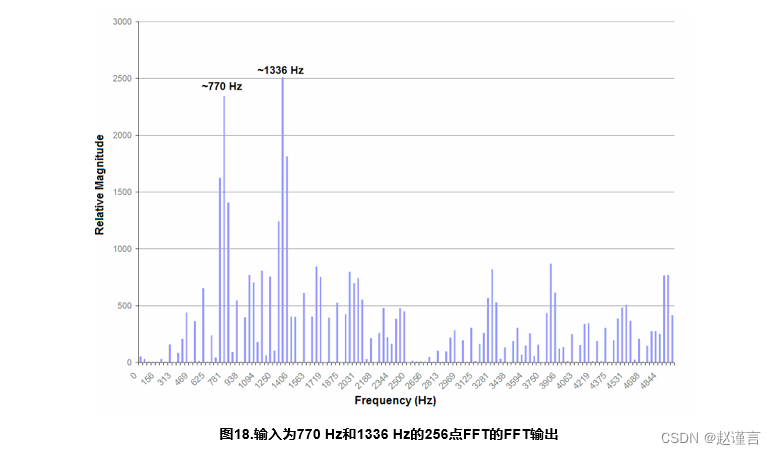
FFT输出表明在输入波形中正确检测到770 Hz和1336 Hz音调。

4.3. 运行FFT演示

FFT演示需要完整版本的Keil编译器（因为代码大小大于4 kB）或SDCC。该固件位于Silicon Labs应用程序网页上的相关应用程序说明软件包中。
有关特定于C8051F120目标板或C8051F360 ToolStick子卡的硬件设置，请参阅"5. 硬件设置”（第22页）.
要重新编译该程序，请打开Silicon Laboratories IDE，然后将FFT_Demo.c文件添加到项目中并进行构建。在项目工具链集成菜单下，选择适当的编译器和可执行文件路径。该项目适用于C8051F120目标板或C8051F360 ToolStick子卡，但可以针对其他平台进行修改。生成项目，连接到目标，然后下载代码。
使用目标板上的RS-232连接器和终端程序（例如超级终端）连接到C8051F120。使用ToolStick终端程序连接到’F360 ToolStick子卡板。将输出保存到文件，然后使用FFT_graph.xls Excel电子表格来绘制输入波形的频率内容（可以在电子表格中找到说明）。

4.4. 性能

在C8051F120和C8051F360上，FFT的MAC实现在25 MHz时比nonMAC实现快8倍，在98 MHz时比non-MAC实现快2倍。

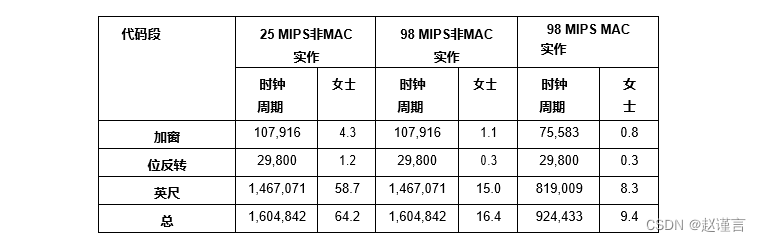
此外，非MAC实现需要5259字节的代码空间和91字节的RAM。MAC实现仅需要4616字节的代码空间和67字节的RAM。MAC的实现不仅速度更快，而且所需资源更少。

5. 硬件设定

硬件设置说明适用于本应用笔记中提供的所有不同示例。

5.1. C8051F120目标板说明

使用J11短路模块将DAC0和AIN0.0引脚连接在一起（J11上的DAC0是引脚3，AIN0.0是引脚7）。此外，验证是否安装了4.7 µF C19和0.1 µC22 VREF电容器，并且J22将VREF引脚上的输出连接至VREF0和VREFD输入引脚。

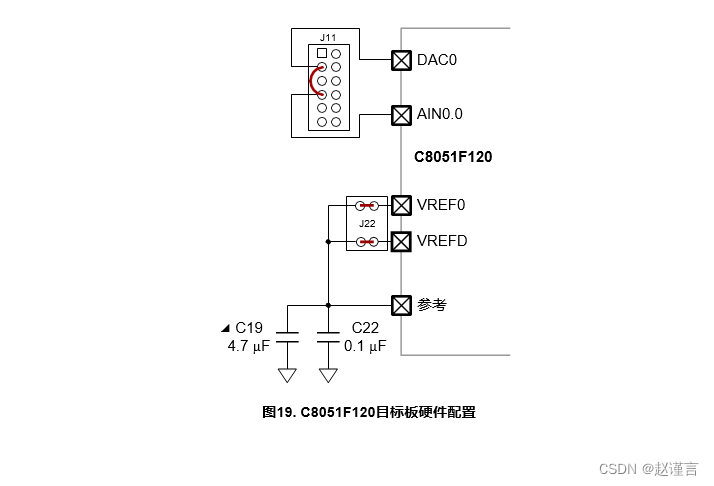
5.2. C8051F360 ToolStick子卡说明

使用板上的测试点将P0.1和P1.1引脚连接在一起。确认已安装R7（1kΩ电阻），C5（0.1 µF电容器）和C1（10µF电容器）。
重要说明：在FIR滤波器示例中使用C8051F36x ToolStick时，请确保将IDAC引脚（P0.1）上的C5 0.1 µF电容器替换为100 pF电容器，以免IDAC正弦波衰减。

---

总结

以上就是今天要讲的内容，本文仅仅简单介绍了在数字信号处理应用中使用微控制器，而数字滤波算法提供了大量能使我们快速便捷地处理数据的算法，详细阐述了数字滤波器算法，Goertzel算法，快速傅立叶变换。