深度优先遍历和广度优先遍历是遍历图的两种常见方式，接下来就通过这两种方式来实现一下图具体遍历的过程

当我位于游乐园的景区 A 时，为了玩遍所有的景区我们有两种玩的方式：

方式一：

• 先依次将景区 A 附近相邻的所有景区（B、C、D）都玩个遍
• 然后依次将景区 B、C、D 附近相邻的所有景区玩个遍
• 以此类推，直到景区都玩遍为止

方式二：

• 先选择一个景区 A 附近相邻的景区（B）进行游玩
• 然后再选择一个景区 B 附近相邻的景区（E）进行游玩
• 一头扎进游乐园，不断的深入，如果发现景区 X 周围的景点都玩过了，就进行回退，回退时如果发现有没有玩过的景区支路，就可以进入该支路继续深入，直到景区都玩遍为止

方式一实际上就是广度优先遍历（B F S）的过程，一层一层的由内而外扩张，遍历的方式有点像二叉树的层序遍历（自上而下）

方式二实际上就是深度优先遍历（D F S）的过程，深度搜索，走到尽头再不断回退找其他可行的支路，遍历的方式有点像二叉树的前中后序遍历

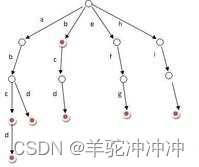
接下来就将具体的通过下面的这张图来形象的展示两种方式遍历图的过程

一、广度优先遍历

广度优先遍历的实现是通过队列完成的

1）我们将从顶点 0 出发，将顶点 0 入队列

2）弹出顶点 0 ，将其附近的顶点1、2、3、4依次遍历放入队列中

3）接着，弹出顶点 1 ，将与其相邻的顶点 8 放入队列中。以此类推，我们将遍历与顶点 2、3、4相邻的未遍历过的顶点，将其添加到队列中

4）最后，将遍历与顶点 8、10、5、6相邻的未遍历过的顶点，依次出队入队

思路：
1、将所有已经遍历过的点都放到一个 set 中
2、将 node 放到 queue 中
3、从队列中弹出一个元素（打印）并将该元素相邻的所有未遍历过的节点都放到 queue 中
4、往复循环，直到 queue 为空，遍历完成

代码实现：

在上一节有介绍过图的标准模板，如果只是完成遍历操作，可以仅保留以下信息

//顶点
public class Node {
    //点的值
    public Integer value;
    //有这个点发散出去的相邻的点有哪些
    public ArrayList<Node> nextNodes;

    public Node(Integer value) {
        this.value = value;
        nextNodes = new ArrayList<>();
    }
}

//图
public class Graph {
    //图中所有的点，key是点的值，value是对应的点的具体信息
    public HashMap<Integer,Node> nodes;

    public Graph() {
        nodes = new HashMap<>();
    }
}

//构造图
public static void main(String[] args) {
    Graph graph = new Graph();
    Node node = new Node(0);
    Node node1 = new Node(1);
    Node node2 = new Node(2);
    Node node3 = new Node(3);
    Node node4 = new Node(4);
    Node node5 = new Node(5);
    Node node6 = new Node(6);
    Node node7 = new Node(7);
    Node node8 = new Node(8);
    Node node9 = new Node(9);
    Node node10 = new Node(10);
    
    node.nextNodes.add(node1);
    node.nextNodes.add(node2);
    node.nextNodes.add(node3);
    node.nextNodes.add(node4);

    node1.nextNodes.add(node);
    node1.nextNodes.add(node2);
    node1.nextNodes.add(node8);

    node2.nextNodes.add(node);
    node2.nextNodes.add(node1);
    node2.nextNodes.add(node10);

    node3.nextNodes.add(node);

    node4.nextNodes.add(node);
    node4.nextNodes.add(node5);
    node4.nextNodes.add(node6);

    node5.nextNodes.add(node4);

    node6.nextNodes.add(node4);
    node6.nextNodes.add(node7);

    node7.nextNodes.add(node6);

    node8.nextNodes.add(node1);
    node8.nextNodes.add(node9);

    node9.nextNodes.add(node10);

    node10.nextNodes.add(node2);
    BFS(node);
}

//广度优先遍历
public void BFS(Node node) {
    if (node == null) {
        return;
    }
    Queue<Node> queue = new LinkedList<>();//一个队列
    HashSet<Node> set = new HashSet<>();//已经遍历过的顶点
    queue.offer(node);
    set.add(node);//添加到已遍历set中
    while (!queue.isEmpty()) {
        Node node1 = queue.poll();//弹出一个元素
        System.out.println(node1.value + " ");//打印元素
        for (Node n: node1.nextNodes) {
            if (!set.contains(n)) {
                //从前未遍历过的
                queue.offer(n);
                set.add(n);//添加到已遍历set中
            }
        }
    }
}

二、深度优先遍历

深度优先遍历的实现是通过栈完成的

1）依次访问顶点 0、1、2、10，依次入栈，此时栈顶是10，表示该支路已经走到了尽头

2）从顶点 10 回溯到顶点 1，依次出栈顶点 10、2

3）在顶点 1 处终于找到了新的支路，依次访问顶点 8、9，依次入栈

4）以此类推，接下来就会出栈顶点 9、8、1，回溯到顶点 0，走顶点 3这条支路，直到遍历完所有的顶点

通过上面的图我们可以明白回溯的过程，那么不断深入的过程又是怎样的呢？如何让栈始终保持的是深度路径？什么情况下出栈？

思路：
1、使用一个栈永远保持着深度的路径 
2、将所有已经遍历过的点都放到一个 set 中
3、将 node 放到栈中，添加到 set 中，进行打印，表示已遍历
4、只要栈不为空，就弹出一个元素
5、弹出的元素，将该元素相邻的没有遍历过的点找到一个后，就不继续找了，break 跳出
6、将弹出的元素以及找的点先后压入栈中，并在 set 中注册找到的点，进行打印，表示已遍历
7、直到所有的点都遍历过了，那么在栈不为空时，栈就只会一直的弹出点，直到栈为空

代码实现：

public static void DFS(Node node) {
    if(node == null) {
        return;
    }
    Stack<Node> stack = new Stack<>();//保持着深度路径的栈
    HashSet<Node> set = new HashSet<>();//已遍历的点
    stack.push(node);
    set.add(node);
    System.out.println(node.value);//打印
    while (!stack.isEmpty()) {
        Node node1 = stack.pop();//弹出一个元素
        for (Node n: node1.nextNodes) {
            if (!set.contains(n)) {
                //找到一个没遍历过的临近的点
                stack.push(node1);//之前弹出的点再压回去
                stack.push(n);//新找到的点压入栈中
                set.add(n);//已遍历该点
                System.out.println(n.value + " ");//打印
                break;//找到一个就跳出，下一轮循环中，再从这个点开始深度遍历
            }
        }
    }
}

当然我们也可以使用递归的方式，毕竟递归的本质就是基于方法调用栈来实现的

public static void DFS2(Node node,HashSet<Node> set) {
    System.out.println(node.value);//打印
    set.add(node);//表示已遍历
    for (Node n:node.nextNodes) {
        if (!set.contains(n)) {
            //找到一个没有遍历过的支路
            DFS2(n,set);
        }
    }
}