给你 n 个长方体 cuboids ，其中第 i 个长方体的长宽高表示为 cuboids[i] = [widthi, lengthi, heighti]（下标从 0 开始）。请你从 cuboids 选出一个 子集 ，并将它们堆叠起来。

如果 widthi <= widthj 且 lengthi <= lengthj 且 heighti <= heightj ，你就可以将长方体 i 堆叠在长方体 j 上。你可以通过旋转把长方体的长宽高重新排列，以将它放在另一个长方体上。

返回 堆叠长方体 cuboids 可以得到的 最大高度 。

 

示例 1：

输入：cuboids = [[50,45,20],[95,37,53],[45,23,12]]
输出：190
解释：
第 1 个长方体放在底部，53x37 的一面朝下，高度为 95 。
第 0 个长方体放在中间，45x20 的一面朝下，高度为 50 。
第 2 个长方体放在上面，23x12 的一面朝下，高度为 45 。
总高度是 95 + 50 + 45 = 190 。

示例 2：

输入：cuboids = [[38,25,45],[76,35,3]]
输出：76
解释：
无法将任何长方体放在另一个上面。
选择第 1 个长方体然后旋转它，使 35x3 的一面朝下，其高度为 76 。

示例 3：

输入：cuboids = [[7,11,17],[7,17,11],[11,7,17],[11,17,7],[17,7,11],[17,11,7]]
输出：102
解释：
重新排列长方体后，可以看到所有长方体的尺寸都相同。
你可以把 11x7 的一面朝下，这样它们的高度就是 17 。
堆叠长方体的最大高度为 6 * 17 = 102 。

 

提示：

    n == cuboids.length
    1 <= n <= 100
    1 <= widthi, lengthi, heighti <= 100

解法一：排序 + 动态规划

首先，若我们枚举所有可能的长方体堆叠的排列组合，便可以很简单的寻找出一个高度和最大的答案。从这个思想出发，我们去观察每一个排列。


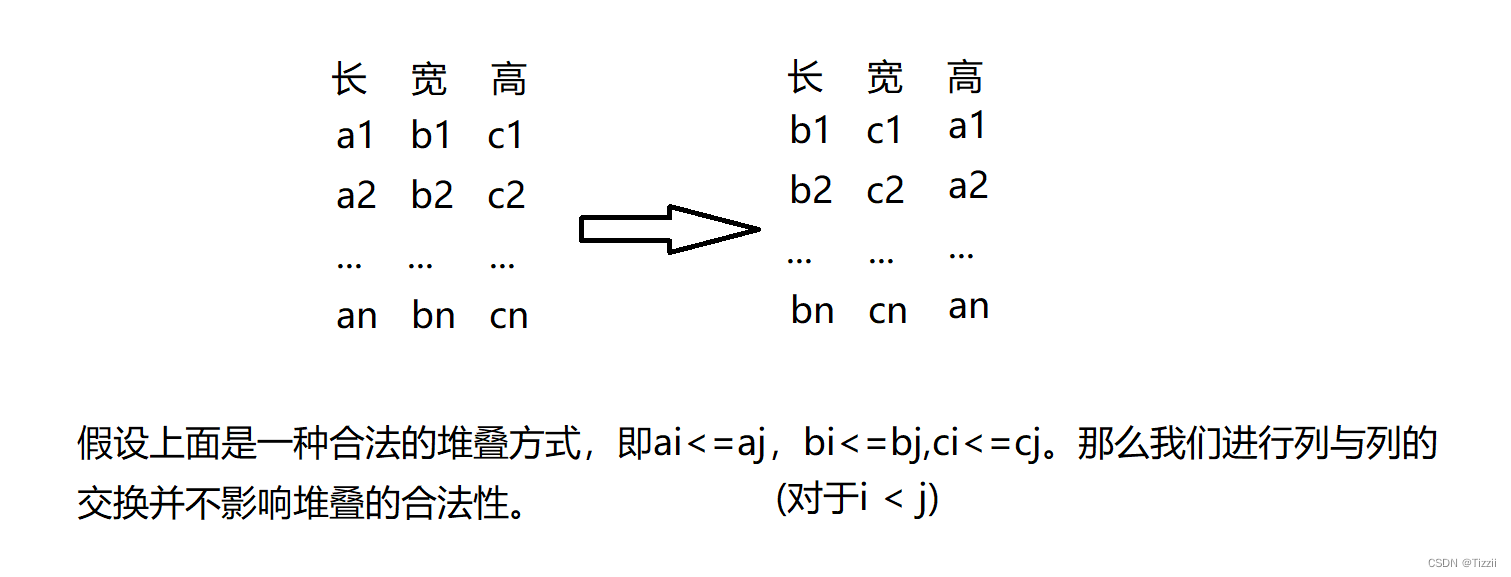不失一般性，我们将第一行的数构造为$a_1\le b_1\le c_1$(通过移动不同的列)

我们从第二列开始构造我们新的堆叠方式：

a1 b1 c1
a2 b2 c2

若$c_2$小于$a_2$或者$b_2$，那么必然能够利用$a_2$和$b_2$中的最大值进行替换使得$c_2$的位置的数变成最大，同理对于$a_2,b_2$,我们也能够使得$b_2$是第二大的值(中位数)。我们便能够将第二行转化为:$a_2\le b_2\le c_2$, 通过移动第2-第n行的列，构造得到的新堆叠方式也是合法的。我们从第一列开始进行不断的移动，直至所有的3元组$(a_i,b_i,c_i)$满足$a_i\le b_i\le c_i$



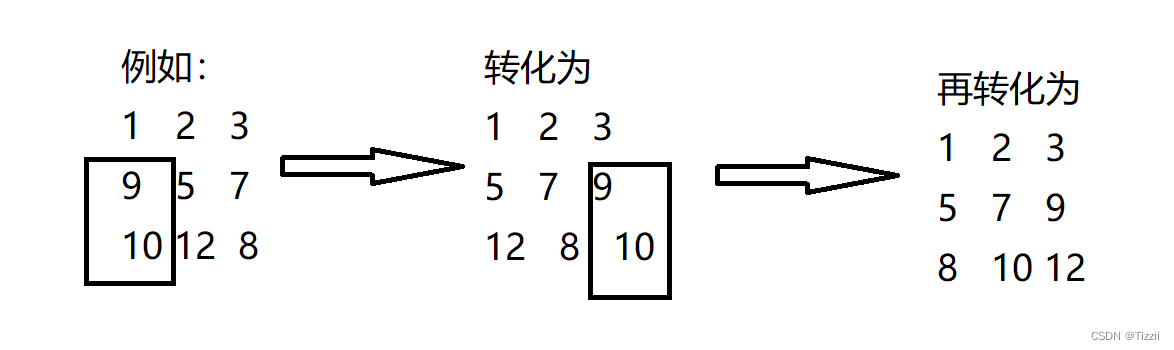
我们可以发现，由于我们将最大的值作为高度，那么通过转化后，最终的结果必然优于以前的排列产生的结果。我们可以对所有有效的堆叠方式进行排列，那么每个长方体的情况转化为（长，宽，高) = (最小值，中位数，最大值）。至此，问题转化为：对于给定n个长方体(长，宽，高），其中长<=宽<=高，求出有效的堆叠方式使得高度和最大。 我们直接按照第一个值从小到大进行排序，若相等按照第二个数继续，直至第三个数。这样排序后，对于某一个长方体$i$来说，能够放在其上面的长方体的索引位置一定在其前面。


至此，这道题目就很简单了，我们不用再去考虑如何进行旋转长方体。那么我们可以轻易的抽象出状态集合，类似于最长递增子序列问题。

 状态集合：
    dp[i]: 以第i个长方体结尾的堆叠方式能够获得的最大高度之和
状态计算：
    dp[i]: max(d[i], dp[j] + height[i]), if ok(i, j) ， 0 <= j < i
    其中ok(i,j)代表hj <= hi, wj <= wi, lj <= li

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(n)$

class Solution {
    public int maxHeight(int[][] cub) {
        int n = cub.length, ans = 0;
        int[] dp = new int[n];
        for (int i = 0; i < n; i++) Arrays.sort(cub[i]);
        Arrays.sort(cub, (a, b) -> a[0] == b[0] ? (a[1] == b[1] ? a[2] - b[2] : a[1] - b[1]) : a[0] - b[0]);//从第一个元素从小到大进行排序，若相等按照第二个元素，若还相等按照第三个元素
        for (int i = 0; i < n; i++) { 
            dp[i] = cub[i][2];
            for (int j = 0; j < i; j++) {
                if (cub[i][1] >= cub[j][1] && cub[i][2] >=  cub[j][2]) dp[i] = Math.max(dp[i], dp[j] + cub[i][2]);
            }
            ans = Math.max(dp[i], ans);
        }
        return ans;
    }
}

class Solution {
public:
    int maxHeight(vector<vector<int>>& cub) {
        int n = cub.size(), ans = 0; 
        vector<int> dp(n, 0);
        for (auto& t : cub) sort(t.begin(), t.end());
        sort(cub.begin(), cub.end(), [](vector<int>& a, vector<int>& b){ return a[0] == b[0] ? (a[1] == b[1] ? a[2] < b[2] : a[1] < b[1]) : a[0] < b[0];});//从第一个元素从小到大进行排序
        for (int i = 0; i < n; i++) { 
            dp[i] = cub[i][2];
            for (int j = 0; j < i; j++) {
                if (cub[i][1] >= cub[j][1] && cub[i][2] >=  cub[j][2]) dp[i] = max(dp[i], dp[j] + cub[i][2]);
            }
            ans = max(dp[i], ans);
        }
        return ans;
    }
};

---

如果有问题,欢迎评论区交流, 如果有帮助到你，请给题解点个赞和收藏哈~~~