🔎大家好，我是Sonhhxg_柒，希望你看完之后，能对你有所帮助，不足请指正！共同学习交流🔎

📝个人主页－Sonhhxg_柒的博客_CSDN博客 📃

🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝

📣系列专栏 - 机器学习【ML】自然语言处理【NLP】深度学习【DL】

🖍foreword

✔说明⇢本人讲解主要包括Python、机器学习（ML）、深度学习（DL）、自然语言处理（NLP）等内容。

如果你对这个系列感兴趣的话，可以关注订阅哟👋

文章目录

创建多臂老虎机环境

怎么做...

这个怎么运作...

使用 epsilon-greedy 策略解决多臂老虎机问题

怎么做...

这个怎么运作...

还有更多...

使用 softmax 探索解决多臂老虎机问题

怎么做...

这个怎么运作...

使用置信上限算法解决多臂老虎机问题

怎么做...

这个怎么运作...

还有更多...

也可以看看

用多臂老虎机解决互联网广告问题

怎么做...

这个怎么运作...

使用 Thompson 采样算法解决多臂老虎机问题

怎么做...

这个怎么运作...

也可以看看

使用上下文强盗解决互联网广告问题

怎么做...

这个怎么运作...

多臂强盗算法可能是强化学习中最流行的算法之一。本章将从创建多臂老虎机和试验随机策略开始。我们将重点介绍如何使用四种策略解决多臂老虎机问题，包括 epsilon-greedy、softmax exploration、置信上限和 Thompson 采样。我们将看到他们如何以自己独特的方式处理探索-开发困境。我们还将研究一个价值数十亿美元的问题，即在线广告，并演示如何使用多臂老虎机算法解决它。最后，我们将使用上下文强盗来解决上下文广告问题，以便在广告优化中做出更明智的决策。

本章将介绍以下食谱：

创建多臂老虎机环境
使用 epsilon-greedy 策略解决多臂老虎机问题
使用 softmax 探索解决多臂老虎机问题
使用置信上限算法解决多臂老虎机问题
用多臂老虎机解决互联网广告问题
使用 Thompson 采样算法解决多臂老虎机问题
使用上下文强盗解决互联网广告问题

创建多臂老虎机环境

让我们从一个简单的项目开始，使用蒙特卡洛方法估计 π 的值，这是无模型强化学习算法的核心。

多臂老虎机问题是最简单的强化学习问题之一。最好将其描述为具有多个杠杆（臂）的老虎机，每个杠杆都有不同的支付和支付概率。我们的目标是找到回报最大的最佳杠杆，以便我们以后可以继续选择它。让我们从一个简单的多臂老虎机问题开始，其中每个臂的支付和支付概率都是固定的。创建环境后，我们将使用随机策略算法对其进行求解。

怎么做...

让我们按如下方式开发多臂老虎机环境：

>>> import torch
>>> class BanditEnv():
...     """
...     Multi-armed bandit environment
...     payout_list:
...         A list of probabilities of the likelihood that a 
            particular bandit will pay out
...     reward_list:
...         A list of rewards of the payout that bandit has
...     """
...     def __init__(self, payout_list, reward_list):
...         self.payout_list = payout_list
...         self.reward_list = reward_list
...
...     def step(self, action):
...         if torch.rand(1).item() < self.payout_list[action]:
...             return self.reward_list[action]
...         return 0

step 方法执行一个动作，如果支付成功则返回奖励，否则返回 0。

现在，我们将以多臂老虎机为例，用随机策略解决它：

1.定义三臂老虎机的支付概率和奖励并创建老虎机环境实例：

>>> bandit_payout = [0.1, 0.15, 0.3]
>>> bandit_reward = [4, 3, 1]
>>> bandit_env = BanditEnv(bandit_payout, bandit_reward)

例如，选择 arm 0 有 10% 的机会获得 4 的奖励。

2.我们指定要运行的剧集数，并定义列表，其中包含通过选择各个臂累积的总奖励、选择各个臂的次数以及每个臂随时间推移的平均奖励：

>>> n_episode = 100000
>>> n_action = len(bandit_payout)
>>> action_count = [0 for _ in range(n_action)]
>>> action_total_reward = [0 for _ in range(n_action)]
>>> action_avg_reward = [[] for action in range(n_action)]

3.定义随机策略，随机选择一个手臂：

>>> def random_policy():
...     action = torch.multinomial(torch.ones(n_action), 1).item()
...     return action

4.现在，我们运行了 100,000 集。对于每一集，我们还更新每个手臂的统计数据：

>>> for episode in range(n_episode):
...     action = random_policy()
...     reward = bandit_env.step(action)
...     action_count[action] += 1
...     action_total_reward[action] += reward
...     for a in range(n_action):
...         if action_count[a]:
...             action_avg_reward[a].append(
                     action_total_reward[a] / action_count[a])
...         else:
...             action_avg_reward[a].append(0)

5.运行 100,000 集后，我们绘制随时间变化的平均奖励结果：

>>> import matplotlib.pyplot as plt
 >>> for action in range(n_action):
 ...     plt.plot(action_avg_reward[action])
 >>> plt.legend([‘Arm {}’.format(action) for action in range(n_action)])
 >>> plt.title(‘Average reward over time’)
 >>> plt.xscale(‘log’)
 >>> plt.xlabel(‘Episode’)
 >>> plt.ylabel(‘Average reward’)
 >>> plt.show()

这个怎么运作...

在我们刚刚处理的示例中，有三台老虎机。每台机器都有不同的支付（奖励）和支付概率。在每一集中，我们随机选择机器的一个手臂来拉动（执行一个动作）并以一定的概率获得回报。

运行第 5 步中的代码行；你会看到下面的情节：

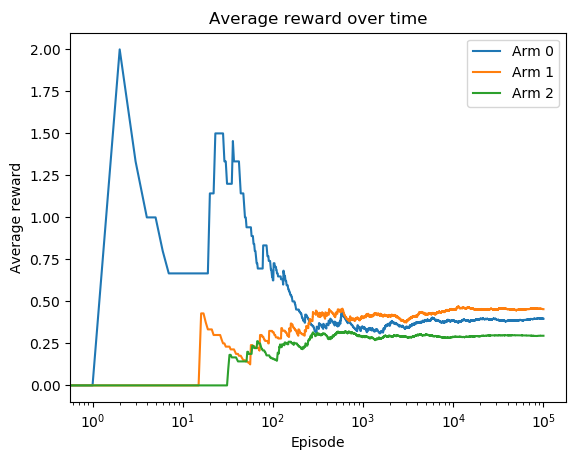
第 1 臂是平均奖励最高的最佳臂。此外，平均奖励在 10,000 集左右开始饱和。

这个解决方案看起来非常幼稚，因为我们只对所有武器进行探索。我们将在接下来的食谱中提出更智能的策略。

使用 epsilon-greedy 策略解决多臂老虎机问题

与其仅仅使用随机策略进行探索，我们还可以结合探索和开发来做得更好。这就是著名的 epsilon-greedy 策略。

多臂老虎机的 Epsilon-greedy 在大部分时间都采用最佳动作，并且不时地探索不同的动作。给定参数 ε，其值从 0 到 1，执行探索和开发的概率分别为 ε 和 1 - ε：

Epsilon：每个动作的执行概率如下：

这里，|A| 是可能动作的数量。

Greedy：state-action value 最高的 action 受到青睐，其被选中的概率增加 1 - ε：

怎么做...

我们使用 epsilon-greedy 策略解决多臂老虎机问题，如下所示：

1.导入 PyTorch 和我们在上一节中开发的 bandit 环境，创建一个多臂 bandit 环境（假设BanditEnv该类位于名为的文件中multi_armed_bandit.py）：

>>> import torch
 >>> from multi_armed_bandit import BanditEnv

2.定义三臂老虎机的支付概率和奖励并创建老虎机环境实例：

>>> bandit_payout = [0.1, 0.15, 0.3]
 >>> bandit_reward = [4, 3, 1]
 >>> bandit_env = BanditEnv(bandit_payout, bandit_reward)

3.我们指定要运行的剧集数，并定义列表，其中包含通过选择各个臂累积的总奖励、选择各个臂的次数以及每个臂随时间推移的平均奖励：

>>> n_episode = 100000
 >>> n_action = len(bandit_payout)
 >>> action_count = [0 for _ in range(n_action)]
 >>> action_total_reward = [0 for _ in range(n_action)]
 >>> action_avg_reward = [[] for action in range(n_action)]

4.定义 epsilon-greedy 策略函数，指定 epsilon 的值，并创建一个 epsilon-greedy 策略实例：

>>> def gen_epsilon_greedy_policy(n_action, epsilon):
 ...     def policy_function(Q):
 ...         probs = torch.ones(n_action) * epsilon / n_action
 ...         best_action = torch.argmax(Q).item()
 ...         probs[best_action] += 1.0 - epsilon
 ...         action = torch.multinomial(probs, 1).item()
 ...         return action
 ...     return policy_function
 >>> epsilon = 0.2
 >>> epsilon_greedy_policy = gen_epsilon_greedy_policy(n_action, epsilon)

5.初始化Q函数，即各个arm获得的平均reward：

>>> Q = torch.zeros(n_action)

我们会随着时间的Q推移更新该功能。

6.现在，我们运行了 100,000 集。对于每一集，我们还更新每个手臂的统计数据：

>>> for episode in range(n_episode):
 ...     action = epsilon_greedy_policy(Q)
 ...     reward = bandit_env.step(action)
 ...     action_count[action] += 1
 ...     action_total_reward[action] += reward
 ...     Q[action] = action_total_reward[action] / action_count[action]
 ...     for a in range(n_action):
 ...         if action_count[a]:
 ...             action_avg_reward[a].append(
                         action_total_reward[a] / action_count[a])
 ...         else:
 ...             action_avg_reward[a].append(0)

7.运行 100,000 集后，我们绘制随时间变化的平均奖励结果：

>>> import matplotlib.pyplot as plt
 >>> for action in range(n_action):
 ...     plt.plot(action_avg_reward[action])
 >>> plt.legend([‘Arm {}’.format(action) for action in range(n_action)])
 >>> plt.title(‘Average reward over time’)
 >>> plt.xscale(‘log’)
 >>> plt.xlabel(‘Episode’)
 >>> plt.ylabel(‘Average reward’)
 >>> plt.show()

这个怎么运作...

与其他 MDP 问题类似，epsilon-greedy 策略以 1 - ε 的概率选择最佳臂，并以 ε 的概率进行随机探索。Epsilon 管理探索和开发之间的权衡。

在第 7 步中，您将看到以下图：

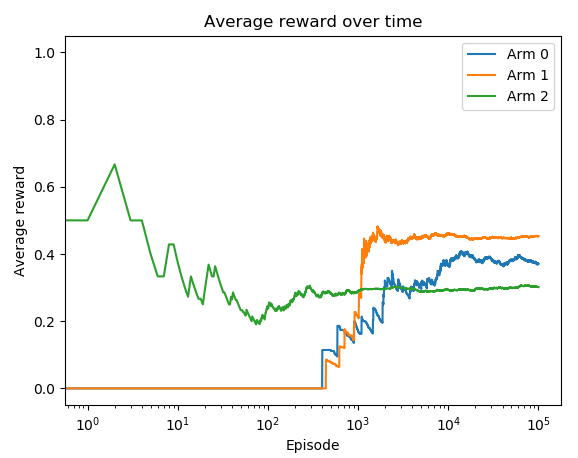
Arm 1 是最好的 arm，最后的平均奖励最高。此外，它的平均奖励在大约 1,000 集后开始饱和。

还有更多...

您可能想知道 epsilon-greedy 策略是否真的优于随机策略。除了最优臂的值在 epsilon-greedy 策略下更早收敛这一事实外，我们还可以证明，平均而言，我们在训练过程中使用 epsilon-greedy 策略获得的奖励高于随机策略。

我们可以简单地对所有情节的奖励进行平均：

>>> print(sum(action_total_reward) / n_episode)
 0.43718

超过 100,000 集，平均支出0.43718采用 epsilon-greedy 策略。对随机策略解决方案重复相同的计算，我们得到 0.37902 作为平均支出。

使用 softmax 探索解决多臂老虎机问题

在这个秘籍中，我们将使用 softmax 探索算法解决多臂老虎机问题。我们将看到它与 epsilon-greedy 策略有何不同。

正如我们在 epsilon-greedy 中看到的那样，在进行探索时，我们随机选择概率为 ε/|A| 的非最佳臂之一。无论其在 Q 函数中的值如何，每个非最佳臂都被同等对待。此外，无论其值如何，都会以固定概率选择最佳臂。在softmax exploration中，基于Q 函数值的softmax 分布的概率选择一个 arm 。概率计算如下：

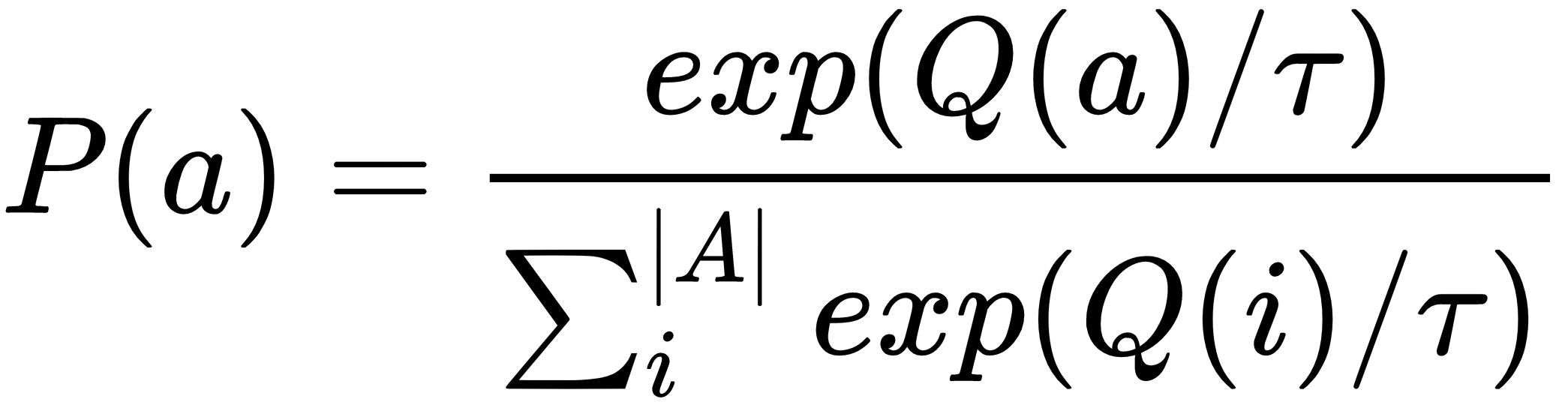
这里，参数 τ 是温度因子，它指定了探索的随机性。τ 的值越大，越接近平等探索；τ 的值越低，选择最佳臂的可能性就越大。

怎么做...

我们使用 softmax 探索算法解决多臂老虎机问题，如下所示：

1.导入 PyTorch 和我们在第一个秘籍中开发的 bandit 环境，创建一个多臂 bandit 环境（假设BanditEnv该类位于名为的文件中multi_armed_bandit.py）：

>>> import torch
 >>> from multi_armed_bandit import BanditEnv

2.定义三臂老虎机的支付概率和奖励并创建老虎机环境实例：

>>> bandit_payout = [0.1, 0.15, 0.3]
 >>> bandit_reward = [4, 3, 1]
 >>> bandit_env = BanditEnv(bandit_payout, bandit_reward)

3.我们指定要运行的剧集数，并定义列表，其中包含通过选择各个臂累积的总奖励、选择各个臂的次数以及每个臂随时间推移的平均奖励：

>>> n_episode = 100000
 >>> n_action = len(bandit_payout)
 >>> action_count = [0 for _ in range(n_action)]
 >>> action_total_reward = [0 for _ in range(n_action)]
 >>> action_avg_reward = [[] for action in range(n_action)]

4.定义 softmax 探索策略函数，指定 τ 的值，并创建一个 softmax 探索策略实例：

>>> def gen_softmax_exploration_policy(tau):
 ...     def policy_function(Q):
 ...         probs = torch.exp(Q / tau)
 ...         probs = probs / torch.sum(probs)
 ...         action = torch.multinomial(probs, 1).item()
 ...         return action
 ...     return policy_function
 >>> tau = 0.1
 >>> softmax_exploration_policy = gen_softmax_exploration_policy(tau)

5.初始化Q函数，即各个arm获得的平均reward：

>>> Q = torch.zeros(n_action)

我们会随着时间更新Q函数。

6.现在，我们运行了 100,000 集。对于每一集，我们还更新每个手臂的统计数据：

>>> for episode in range(n_episode):
 ...     action = softmax_exploration_policy(Q)
 ...     reward = bandit_env.step(action)
 ...     action_count[action] += 1
 ...     action_total_reward[action] += reward
 ...     Q[action] = action_total_reward[action] / action_count[action]
 ...     for a in range(n_action):
 ...         if action_count[a]:
 ...             action_avg_reward[a].append(
                         action_total_reward[a] / action_count[a])
 ...         else:
 ...             action_avg_reward[a].append(0)

7.运行 100,000 集后，我们绘制随时间变化的平均奖励结果：

>>> import matplotlib.pyplot as plt
 >>> for action in range(n_action):
 ...     plt.plot(action_avg_reward[action])
 >>> plt.legend([‘Arm {}’.format(action) for action in range(n_action)])
 >>> plt.title(‘Average reward over time’)
 >>> plt.xscale(‘log’)
 >>> plt.xlabel(‘Episode’)
 >>> plt.ylabel(‘Average reward’)
 >>> plt.show()

这个怎么运作...

借助softmax探索策略，利用基于Q值的softmax函数解决了开发和探索的困境。它不是对最佳臂和非最佳臂使用一对固定的概率，而是根据以 τ 参数作为温度因子的 softmax 分布来调整概率。τ 的值越高，将越多的注意力转移到探索上。

在第 7 步中，您将看到以下图：

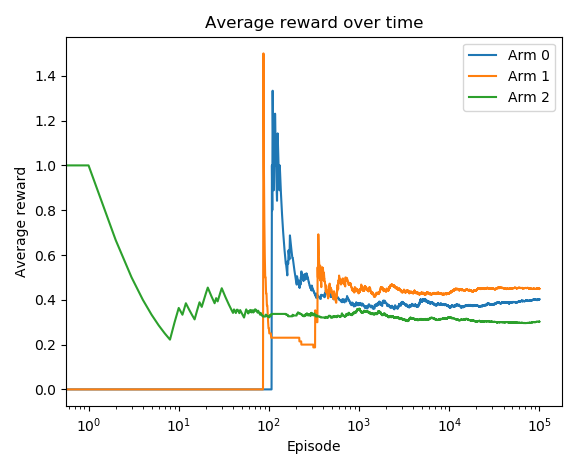
Arm 1 是最好的 arm，最后的平均奖励最高。此外，在这个例子中，它的平均奖励在大约 800 集之后开始饱和。

使用置信上限算法解决多臂老虎机问题

在前两个秘籍中，我们探索了多臂老虎机问题中的随机动作，概率要么在 epsilon-greedy 策略中指定为固定值，要么在 softmax 探索算法中根据 Q 函数值计算。在任何一种算法中，采取随机行动的概率都不会随时间调整。理想情况下，随着学习的进展，我们希望减少探索。在这个秘籍中，我们将使用一种称为置信上限的新算法来实现这一目标。

置信上限( UCB ) 算法源于置信区间的概念。通常，置信区间是真实值所在的值范围。在 UCB 算法中，手臂的置信区间是该手臂获得的平均奖励所在的范围。区间的形式是[置信下限，置信上限]，我们只使用上限，也就是UCB，来估计手臂的潜力。UCB 计算如下：

这里，t 是 episode 的数量，N(a) 是 arm a 在 t episode 中被选择的次数。随着学习的进行，置信区间缩小并变得越来越准确。要拉的手臂是具有最高 UCB 的手臂。

怎么做...

我们使用 UCB 算法解决多臂老虎机问题，如下所示：

1.导入 PyTorch 和我们在第一个秘籍中开发的 bandit 环境，创建一个多臂 bandit 环境（假设BanditEnv该类位于名为的文件中multi_armed_bandit.py）：

>>> import torch
 >>> from multi_armed_bandit import BanditEnv

2.定义三臂老虎机的支付概率和奖励并创建老虎机环境实例：

>>> bandit_payout = [0.1, 0.15, 0.3]
 >>> bandit_reward = [4, 3, 1]
 >>> bandit_env = BanditEnv(bandit_payout, bandit_reward)

3.我们指定要运行的剧集数，并定义列表，其中包含通过选择各个臂累积的总奖励、选择各个臂的次数以及每个臂随时间推移的平均奖励：

>>> n_episode = 100000
 >>> n_action = len(bandit_payout)
 >>> action_count = torch.tensor([0. for _ in range(n_action)])
 >>> action_total_reward = [0 for _ in range(n_action)]
 >>> action_avg_reward = [[] for action in range(n_action)]

4.定义 UCB 策略函数，它根据 UCB 公式计算最佳臂：

>>> def upper_confidence_bound(Q, action_count, t):
 ...     ucb = torch.sqrt((2 * torch.log(torch.tensor(float(t)))) 
                                             / action_count) + Q
 ...     return torch.argmax(ucb)

5.初始化 Q 函数，它是单个手臂获得的平均奖励：

>>> Q = torch.empty(n_action)

我们会随着时间更新Q函数。

6.现在，我们使用 UCB 策略运行了 100,000 集。对于每一集，我们还更新每个手臂的统计数据：

>>> for episode in range(n_episode):
 ...     action = upper_confidence_bound(Q, action_count, episode)
 ...     reward = bandit_env.step(action)
 ...     action_count[action] += 1
 ...     action_total_reward[action] += reward
 ...     Q[action] = action_total_reward[action] / action_count[action]
 ...     for a in range(n_action):
 ...         if action_count[a]:
 ...             action_avg_reward[a].append(
                         action_total_reward[a] / action_count[a])
 ...         else:
 ...             action_avg_reward[a].append(0)

7.运行 100,000 集后，我们绘制随时间变化的平均奖励结果：

>>> import matplotlib.pyplot as plt
 >>> for action in range(n_action):
 ...     plt.plot(action_avg_reward[action])
 >>> plt.legend([‘Arm {}’.format(action) for action in range(n_action)])
 >>> plt.title(‘Average reward over time’)
 >>> plt.xscale(‘log’)
 >>> plt.xlabel(‘Episode’)
 >>> plt.ylabel(‘Average reward’)
 >>> plt.show()

这个怎么运作...

在这个秘籍中，我们用 UCB 算法解决了多臂老虎机。它根据情节的数量调整开发-探索困境。对于数据点较少的动作，其置信区间比较宽，因此选择该动作具有较高的不确定性。随着选择的动作的更多情节，置信区间变窄并缩小到其实际值。在这种情况下，选择（或不选择）这个动作的确定性很高。最后，UCB 算法在每一集中拉动具有最高 UCB 的手臂，并随着时间的推移获得越来越多的信心。

运行第 7 步中的代码后，您将看到以下图：

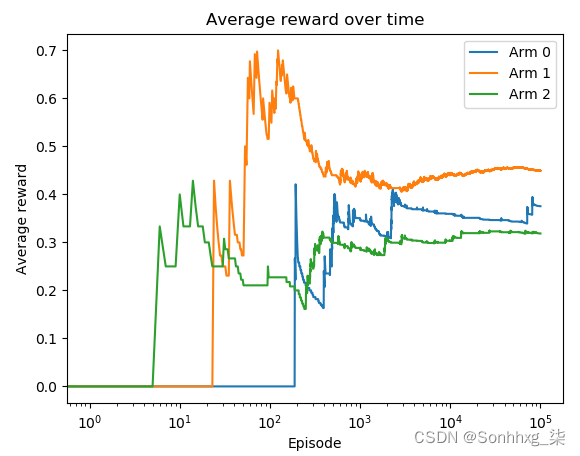
Arm 1 是最好的 arm，最终平均奖励最高。

还有更多...

您可能想知道 UCB 是否真的优于 epsilon-greedy 策略。我们可以计算整个训练过程的平均奖励，平均奖励最高的策略学得更快。

我们可以简单地对所有情节的奖励进行平均：

>>> print(sum(action_total_reward) / n_episode)
 0.44605

超过 100,000 集时，UCB 的平均支出为 0.44605，高于 epsilon-greedy 策略的 0.43718。

也可以看看

对于那些想要复习置信区间的人，请随时查看以下内容：http: //www.stat.yale.edu/Courses/1997-98/101/confint.htm

用多臂老虎机解决互联网广告问题

想象一下，您是一位致力于网站广告优化的广告商：

广告背景有红色、绿色和蓝色三种不同颜色。哪一个将获得最佳点击率 (CTR)？
广告的措辞分为三种类型——学习……、免费……和尝试……。哪一个将获得最佳点击率？

对于每个访问者，我们需要选择一个广告，以便随着时间的推移最大化点击率。我们如何解决这个问题？

也许您正在考虑 A/B 测试，您将流量随机分组并将每个广告分配到不同的组，然后在观察一段时间后从 CTR 最高的组中选择广告。然而，这基本上是一个完整的探索，我们通常不确定观察期应该有多长，最终会失去很大一部分潜在点击。此外，在 A/B 测试中，假设广告的未知点击率不会随时间变化。否则，应定期重新运行此类 A/B 测试。

多臂老虎机肯定比 A/B 测试做得更好。每个手臂都是一个广告，手臂的奖励是 1（点击）或 0（无点击）。

让我们尝试用 UCB 算法来解决它。

怎么做...

我们可以使用 UCB 算法解决多臂强盗广告问题，如下所示：

1.导入 PyTorch 和我们在第一个秘籍中开发的 bandit 环境，创建一个多臂 bandit 环境（假设BanditEnv类在一个名为的文件中multi_armed_bandit.py）：

>>> import torch
>>> from multi_armed_bandit import BanditEnv

2.定义三臂老虎机（例如三个广告候选者）的支付概率和奖励并创建老虎机环境实例：

>>> bandit_payout = [0.01, 0.015, 0.03]
>>> bandit_reward = [1, 1, 1]
>>> bandit_env = BanditEnv(bandit_payout, bandit_reward)

此处，广告 0 的真实点击率为 1%，广告 1 为 1.5%，广告 2 为 3%。

3.我们指定要运行的剧集数，并定义列表，其中包含通过选择各个臂累积的总奖励、选择各个臂的次数以及每个臂随时间推移的平均奖励：

>>> n_episode = 100000
>>> n_action = len(bandit_payout)
>>> action_count = torch.tensor([0. for _ in range(n_action)])
>>> action_total_reward = [0 for _ in range(n_action)]
>>> action_avg_reward = [[] for action in range(n_action)]

4.定义 UCB 策略函数，它根据 UCB 公式计算最佳臂：

>>> def upper_confidence_bound(Q, action_count, t):
...     ucb = torch.sqrt((2 * torch.log(
                    torch.tensor(float(t)))) / action_count) + Q
...     return torch.argmax(ucb)

5.初始化Q函数，即各个arm获得的平均reward：

>>> Q = torch.empty(n_action)

我们会随着时间更新Q函数。

6.现在，我们使用 UCB 策略运行了 100,000 集。对于每一集，我们还更新每个手臂的统计数据：

>>> for episode in range(n_episode):
...     action = upper_confidence_bound(Q, action_count, episode)
...     reward = bandit_env.step(action)
...     action_count[action] += 1
...     action_total_reward[action] += reward
...     Q[action] = action_total_reward[action] / action_count[action]
...     for a in range(n_action):
...         if action_count[a]:
...             action_avg_reward[a].append(
                    action_total_reward[a] / action_count[a])
...         else:
...             action_avg_reward[a].append(0)

7.运行 100,000 集后，我们绘制随时间变化的平均奖励结果：

>>> import matplotlib.pyplot as plt
>>> for action in range(n_action):
...     plt.plot(action_avg_reward[action])
>>> plt.legend([‘Arm {}’.format(action) for action in range(n_action)])
>>> plt.title(‘Average reward over time’)
>>> plt.xscale(‘log’)
>>> plt.xlabel(‘Episode’)
>>> plt.ylabel(‘Average reward’)
>>> plt.show()

这个怎么运作...

在这个秘籍中，我们以多臂老虎机的方式解决了广告优化问题。它克服了 A/B 测试方法面临的挑战。我们使用 UCB 算法来解决多臂（multi-ad）老虎机问题；每个手臂的奖励要么是 1 要么是 0。UCB（或其他算法，如 epsilon-greedy 和 softmax 探索）不是纯粹的探索，也不是行动和奖励之间的交互，而是在必要的地方动态地在开发和探索之间切换。对于数据点少的广告，置信区间比较宽，因此选择这个动作的不确定性比较高。随着更多广告片段被选中，置信区间变窄并缩小到其实际值。

您可以在步骤 7中看到结果图，如下所示：

广告 2 是模型收敛后预测 CTR（平均奖励）最高的最佳广告。

最终，我们发现广告 2 是最佳选择，这是事实。此外，我们越早弄清楚这一点越好，因为我们失去的潜在点击次数会更少。在此示例中，广告 2 在大约 100 集后表现优于其他广告。

使用 Thompson 采样算法解决多臂老虎机问题

在这个秘籍中，我们将使用另一种算法 Thompson 抽样来解决广告强盗问题中的利用和探索困境。我们将看到它与前三种算法有何不同。

Thompson sampling ( TS ) 也被称为 Bayesian bandits，因为它从以下角度应用贝叶斯思维方式：

它是一种概率算法。
它计算每个臂的先验分布并从每个分布中采样一个值。
然后它选择具有最高价值的手臂并观察奖励。
最后，它根据观察到的奖励更新先验分布。这个过程称为贝叶斯更新。

正如我们所见，在我们的广告优化案例中，每个臂的奖励为 1 或 0。我们可以将beta 分布用于我们的先验分布，因为 beta 分布的值是从 0 到 1。beta 分布由以下参数化两个参数，α 和 β。α表示我们获得1的奖励的次数，β表示我们获得0的奖励的次数。

为了帮助您更好地理解 beta 分布，我们将在实现 TS 算法之前先查看几个 beta 分布。

怎么做...

让我们通过以下步骤探索 beta 分布：

1.导入 PyTorch 和 matplotlib，因为我们将可视化分布的形状：

>>> import torch
>>> import matplotlib.pyplot as plt

2.我们首先可视化具有起始位置 α=1 和 β=1 的 beta 分布的形状：

>>> beta1 = torch.distributions.beta.Beta(1, 1) 
>>> samples1 = [beta1.sample() for _ in range(100000)] 
>>> plt.hist(samples1, range=[0, 1], bins=10) 
>>> plt.title('beta(1, 1)') 
>>> plt.show()

您将看到以下情节：

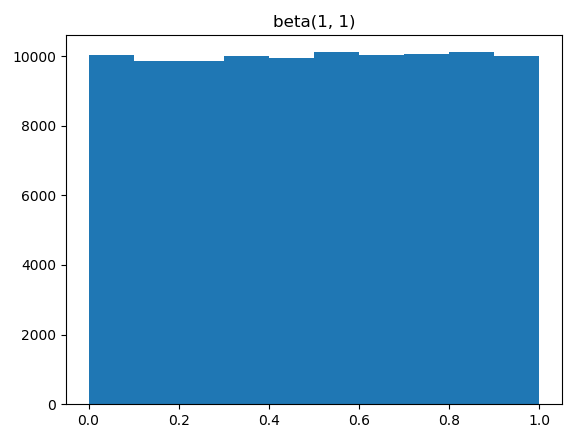
显然，当 α=1 和 β=1 时，它不提供任何关于真实值在 0 到 1 范围内的信息。因此，它成为均匀分布。

3.然后我们可视化 α=5 和 β=1 的 beta 分布的形状：

>>> beta2 = torch.distributions.beta.Beta(5, 1) 
>>> samples2 = [beta2.sample() for _ in range(100000)] 
>>> plt.hist(samples2, range=[0, 1], bins=10) 
>>> plt.title('beta(5, 1)') 
>>> plt.show()

您将看到以下情节：

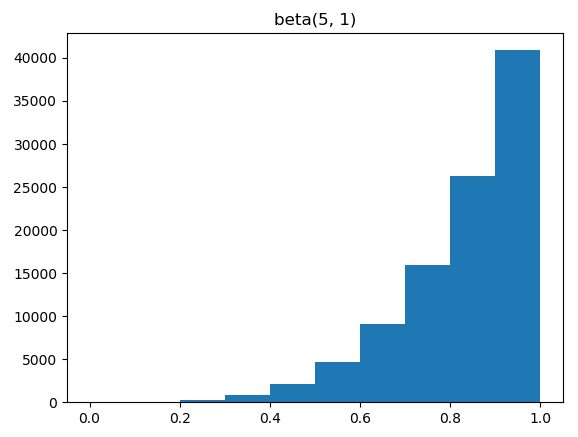
当α=5，β=1时，这意味着4次实验中有4次连续奖励1次。分布向 1 移动。

4.现在，让我们用 α=1 和 β=5 进行实验：

>>> beta3 = torch.distributions.beta.Beta(1, 5) 
>>> samples3= [beta3.sample() for _ in range(100000)] 
>>> plt.hist(samples3, range=[0, 1], bins=10) 
>>> plt.title('beta(1, 5)') 
>>> plt.show()

您将看到以下情节：

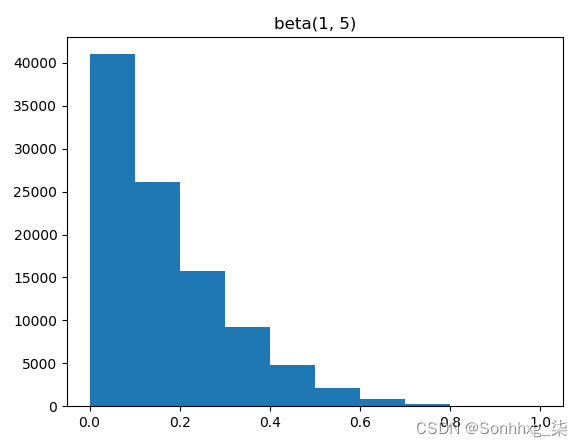
当α=1，β=5时，这意味着在4次实验中有4次连续的奖励为0。分布向 0 移动。

5.最后，我们看一下α=5，β=5时的情况：

>>> beta4 = torch.distributions.beta.Beta(5, 5) 
>>> samples4= [beta4.sample() for _ in range(100000)] 
>>> plt.hist(samples4, range=[0, 1], bins=10) 
>>> plt.title('beta(5, 5)') 
>>> plt.show()

您将看到以下情节：

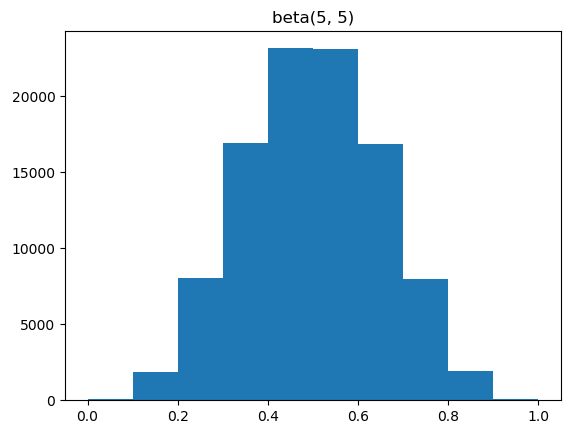
当 α=5 和 β=5 时，我们在 8 轮中观察到相同数量的点击和未点击。分布向中间点0.5移动。

现在是时候使用 Thompson 采样算法解决多臂强盗广告问题了：

1.导入我们在第一个秘籍中开发的 bandit 环境，创建一个多臂 bandit 环境（假设BanditEnv类在一个名为的文件中multi_armed_bandit.py）：

>>> from multi_armed_bandit import BanditEnv

2.定义三臂老虎机（三个广告候选者）的支付概率和奖励并创建老虎机环境实例：

>>> bandit_payout = [0.01, 0.015, 0.03]
>>> bandit_reward = [1, 1, 1]
>>> bandit_env = BanditEnv(bandit_payout, bandit_reward)

3.我们指定要运行的剧集数，并定义列表，其中包含通过选择各个臂累积的总奖励、选择各个臂的次数以及每个臂随时间推移的平均奖励：

>>> n_episode = 100000
>>> n_action = len(bandit_payout)
>>> action_count = torch.tensor([0. for _ in range(n_action)])
>>> action_total_reward = [0 for _ in range(n_action)]
>>> action_avg_reward = [[] for action in range(n_action)]

4.定义 TS 函数，它从每个臂的 beta 分布中采样一个值，并选择具有最高值的臂：

>>> def thompson_sampling(alpha, beta):
...     prior_values = torch.distributions.beta.Beta(alpha, beta).sample()
...     return torch.argmax(prior_values)

5.为每个臂初始化 α 和 β：

>>> alpha = torch.ones(n_action) 
>>> beta = torch.ones(n_action)

请注意，每个 beta 分布都应以 α=β=1 开头。

6.现在，我们使用 TS 算法运行 100,000 集。对于每一集，我们还根据观察到的奖励更新每个臂的 α 和 β ：

>>> for episode in range(n_episode):
 ...     action = thompson_sampling(alpha, beta)
 ...     reward = bandit_env.step(action)
 ...     action_count[action] += 1
 ...     action_total_reward[action] += reward
 ...     if reward > 0:
 ...         alpha[action] += 1
 ...     else:
 ...         beta[action] += 1
 ...     for a in range(n_action):
 ...         if action_count[a]:
 ...             action_avg_reward[a].append(    
                     action_total_reward[a] / action_count[a])
 ...         else:
 ...             action_avg_reward[a].append(0)

7.运行 100,000 集后，我们绘制随时间变化的平均奖励结果：

>>> import matplotlib.pyplot as plt
>>> for action in range(n_action):
...     plt.plot(action_avg_reward[action])
>>> plt.legend([‘Arm {}’.format(action) for action in range(n_action)])
>>> plt.title(‘Average reward over time’)
>>> plt.xscale(‘log’)
>>> plt.xlabel(‘Episode’)
>>> plt.ylabel(‘Average reward’)
>>> plt.show()

这个怎么运作...

在这个秘籍中，我们用 TS 算法解决了广告强盗问题。TS 与其他三种方法的最大区别在于采用了贝叶斯优化。它首先计算每个可能臂的先验分布，然后从每个分布中随机抽取一个值。然后它选择具有最高值的手臂并使用观察到的结果来更新先验分布。TS 策略既是随机的又是贪婪的。如果广告更有可能获得点击，则其 Beta 分布会向 1 移动，因此随机样本的值往往更接近 1。

运行第 7 步中的代码行后，您将看到以下图：

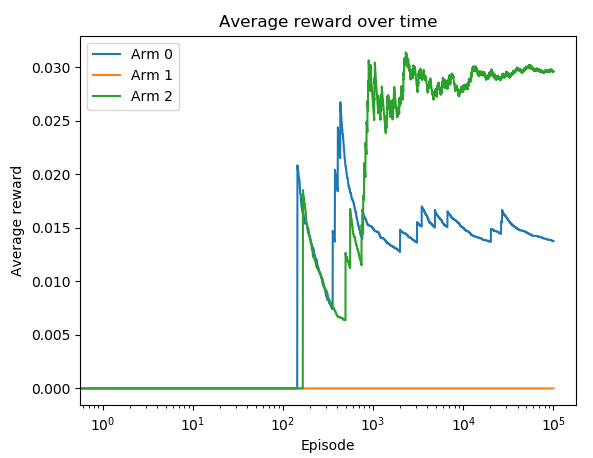
广告 2 是最好的广告，具有最高的预测 CTR（平均奖励）。

也可以看看

对于那些想要重温 Beta 发行版的人，请随时查看以下内容：

1.3.6.6.17. Beta Distribution
Understanding the beta distribution (using baseball statistics) – Variance Explained

使用上下文强盗解决互联网广告问题

你可能会注意到，在广告优化问题中，我们只关心广告，而忽略了其他可能影响广告被点击与否的信息，例如用户信息和网页信息。在这个秘籍中，我们将讨论如何考虑广告本身以外的更多信息并解决上下文强盗的问题。

到目前为止，我们处理的多臂老虎机问题不涉及状态的概念，这与 MDP 有很大不同。我们只有几个动作，并且将生成与所选动作相关联的奖励。Contextual bandits通过引入状态的概念来扩展多臂 bandits。状态提供了对环境的描述，这有助于代理采取更明智的行动。在广告示例中，状态可以是用户的性别（两个状态，男性和女性）、用户的年龄组（例如四个状态）或页面类别（例如体育、金融或新闻）。直觉上，某些人口统计数据的用户更有可能点击某些页面上的广告。

不难理解contextual bandits。多臂老虎机是一台有多个手臂的机器，而上下文老虎机是一组这样的机器（老虎机）。contextual bandits 中的每台机器都是一个拥有多个武器的状态。学习目标是为每个机器（状态）找到最好的手臂（动作）。

为简单起见，我们将使用具有两个状态的广告示例。

怎么做...

我们使用 UCB 算法解决上下文强盗广告问题，如下所示：

1.导入 PyTorch 和我们在第一个秘籍中开发的 bandit 环境，创建一个多臂 bandit 环境（假设BanditEnv类在一个名为的文件中multi_armed_bandit.py）：

>>> import torch
>>> from multi_armed_bandit import BanditEnv

2.定义两个三臂强盗的支付概率和奖励：

>>> bandit_payout_machines = [
...     [0.01, 0.015, 0.03],
...     [0.025, 0.01, 0.015]
... ]
>>> bandit_reward_machines = [
...     [1, 1, 1],
...     [1, 1, 1]
... ]

在这里，广告 0 的真实点击率是 1%，广告 1 的真实点击率是 1.5%，广告 2 的第一个状态是 3%，第二个状态是 [2.5%、1% 和 1.5%]。

在我们的例子中，老虎机的数量是两个：

>>> n_machine = len(bandit_payout_machines)

给定相应的支出信息，创建强盗列表：

>>> bandit_env_machines = [BanditEnv(bandit_payout, bandit_reward) 
... for bandit_payout, bandit_reward in 
... zip(bandit_payout_machines, bandit_reward_machines)]

3.我们指定要运行的 episode 数，并定义列表，其中包含在每个状态下选择单个臂累积的总奖励、每个状态下选择单个臂的次数，以及每个状态下每个臂随时间推移的平均奖励：

>>> n_episode = 100000
>>> n_action = len(bandit_payout_machines[0])
>>> action_count = torch.zeros(n_machine, n_action)
>>> action_total_reward = torch.zeros(n_machine, n_action)
>>> action_avg_reward = [[[] for action in range(n_action)] for _ in range(n_machine)]

4.定义 UCB 策略函数，它根据 UCB 公式计算最佳臂：

>>> def upper_confidence_bound(Q, action_count, t):
...     ucb = torch.sqrt((2 * torch.log(  
                 torch.tensor(float(t)))) / action_count) + Q
...     return torch.argmax(ucb)

5.初始化 Q 函数，它是各个状态下各个臂获得的平均奖励：

>>> Q_machines = torch.empty(n_machine, n_action)

我们将随时间更新 Q 函数。

6.现在，我们使用 UCB 策略运行了 100,000 集。对于每一集，我们还更新每个状态下每个手臂的统计数据：

>>> for episode in range(n_episode):
...     state = torch.randint(0, n_machine, (1,)).item()
...     action = upper_confidence_bound(
                 Q_machines[state], action_count[state], episode)
...     reward = bandit_env_machines[state].step(action)
...     action_count[state][action] += 1
...     action_total_reward[state][action] += reward
...     Q_machines[state][action] = 
                             action_total_reward[state][action] 
                             / action_count[state][action]
...     for a in range(n_action):
...         if action_count[state][a]:
...             action_avg_reward[state][a].append(
                             action_total_reward[state][a] 
                             / action_count[state][a])
...         else:
...             action_avg_reward[state][a].append(0)

7.运行 100,000 集后，我们绘制每个状态随时间变化的平均奖励结果：

>>> import matplotlib.pyplot as plt
>>> for state in range(n_machine):
...     for action in range(n_action):
...         plt.plot(action_avg_reward[state][action])
...     plt.legend([‘Arm {}’.format(action) 
                     for action in range(n_action)])
...     plt.xscale(‘log’)
...     plt.title(
       ‘Average reward over time for state {}’.format(state))
...     plt.xlabel(‘Episode’)
...     plt.ylabel(‘Average reward’)
...     plt.show()

这个怎么运作...

在这个秘籍中，我们使用 UCB 算法解决了上下文强盗的上下文广告问题。

运行第 7 步中的代码行，您将看到以下图表。

我们得到第一个状态：

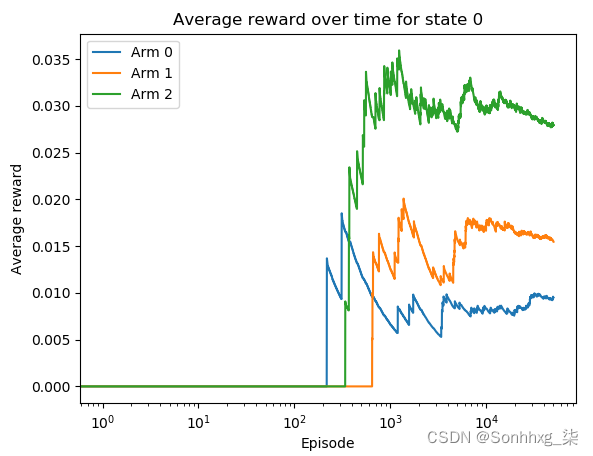
我们得到了第二个状态：

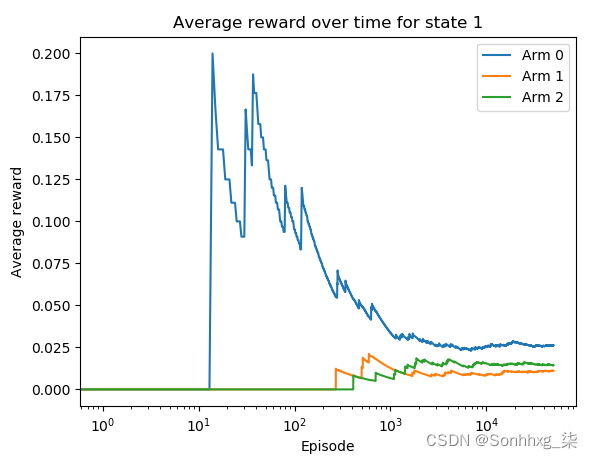
给定第一个状态，广告 2 是最好的广告，具有最高的预测点击率。给定第二个状态，广告 0 是最佳广告，具有最高的平均奖励。这些都是真的。

上下文强盗是一组多臂强盗。每个强盗代表一个独特的环境状态。状态提供了对环境的描述，这有助于代理采取更明智的行动。在我们的广告示例中，男性用户可能比女性用户更有可能点击广告。我们简单地使用了两个老虎机来合并两个状态，并在给定每个状态的情况下搜索最好的手臂来拉动。

需要注意的一件事是，contextual bandits 仍然不同于 MDP，尽管它们涉及状态的概念。首先，contextual bandits 中的状态不是由先前的动作或状态决定的，而只是对环境的观察。其次，在上下文老虎机中没有延迟或打折的奖励，因为老虎机情节是一个步骤。然而，与多臂老虎机相比，上下文老虎机更接近 MDP，因为这些动作以环境中的状态为条件。可以肯定地说，contextual bandits 介于 multi-armed bandits 和完整的 MDP 强化学习之间。