全文链接:http://tecdat.cn/?p=24182
本文用 R 编程语言极值理论 (EVT) 以确定 10 只股票指数的风险价值(和条件 VaR)(点击文末“阅读原文”获取完整代码数据)。
使用 Anderson-Darling 检验对 10 只股票的组合数据进行正态性检验,并使用 Block Maxima 和 Peak-Over-Threshold 的 EVT 方法估计 VaR/CvaR。最后,使用条件异向性 (GARCH) 处理的广义自回归来预测未来 20 天后指数的未来值。本文将确定计算风险因素的不同方法对模型结果的影响。
相关视频
极值理论(最初由Fisher、Tippett和Gnedenko提出)表明,独立同分布(iid)变量样本的分块最大值的分布会收敛到三个极值分布之一。
最近,统计学家对极端值建模的兴趣又有了新的变化。极限值分析已被证明在各种风险因素的案例中很有用。在1999年至2008年的金融市场动荡之后,极值分析获得了有效性,与之前的风险价值分析不同。极限值代表一个系统的极端波动。极限值分析提供了对极端事件的概率、规模和保护成本的关系进行建模的能力。
参考
https://arxiv.org/pdf/1310.3222.pdf
https://www.ma.utexas.edu/mp_arc/c/11/11-33.pdf
http://evt2013.weebly.com/uploads/1/2/6/9/12699923/penalva.pdf
Risk Measurement in Commodities Markets Using Conditional Extreme Value Theory
第 1a 节 - 工作目录、所需的包和会话信息
为了开始分析,工作目录被设置为包含股票行情的文件夹。然后,安装所需的 R 编程语言包并包含在包库中。R 包包括极值理论函数、VaR 函数、时间序列分析、定量交易分析、回归分析、绘图和 html 格式的包。
library(ggplot2)
library(tseries)
library(vars)
library(evd)
library(POT)
library(rugarch)第 1b 节 - 格式化专有数据
用于此分析的第一个文件是“Data_CSV.csv”。该文件包含在 DAX 证券交易所上市的 15 家公司的股票代码数据,以及 DAX 交易所的市场投资组合数据。从这个数据文件中选出了 10 家公司,这些公司最近十年的股价信息是从谷歌财经下载的。

第 1c 节 - 下载股票代码数据
股票价格数据下载并读入 R 编程环境。收益率是用“开盘价/收盘价 ”计算的,十家公司的数据合并在一个数据框中,(每家公司一列)。
结果数据帧的每一行代表记录股价的 10 年中的一个工作日。然后计算数据帧中每一行的均值。一列 10 年的日期被附加到数据框。还创建了仅包含行均值和日期信息的第二个数据框。
alDat <- cbind(retursDaa, returnDta_A,
retrnsata_Ss, reunsataDB,
retunsDta\_H, reurnsDta\_S, rtunsDaaA,
retrnsaa_senus,reursDtaAlnz,
reurnsData_ailer)第 2a 节 - 探索性数据分析
创建一个数据框统计表,其中包含每列(或公司)的最小值、中值、平均值、最大值、标准偏差、1% 分位数、5% 分位数、95% 分位数、99% 分位数。分位数百分比适用于极值。还创建了所有收益率均值的时间序列图表。
taeSs<- c(min(x), medan(x), man(x),
max(x), sd(x), quntile(x, .01),
quanile(x, .05), qunile(x, .95),
quatile(x, .99), lngth(x))
第 2b 节 - 10 只股票指数的 VaR 估计
all_va.2 <- VAR(lDvarts, p = 2, tpe= "cnst")
# 预测未来125天、250天和500天
aDFva100 <- pdc(alDva.c, n.aea = 100, ci = 0.9)
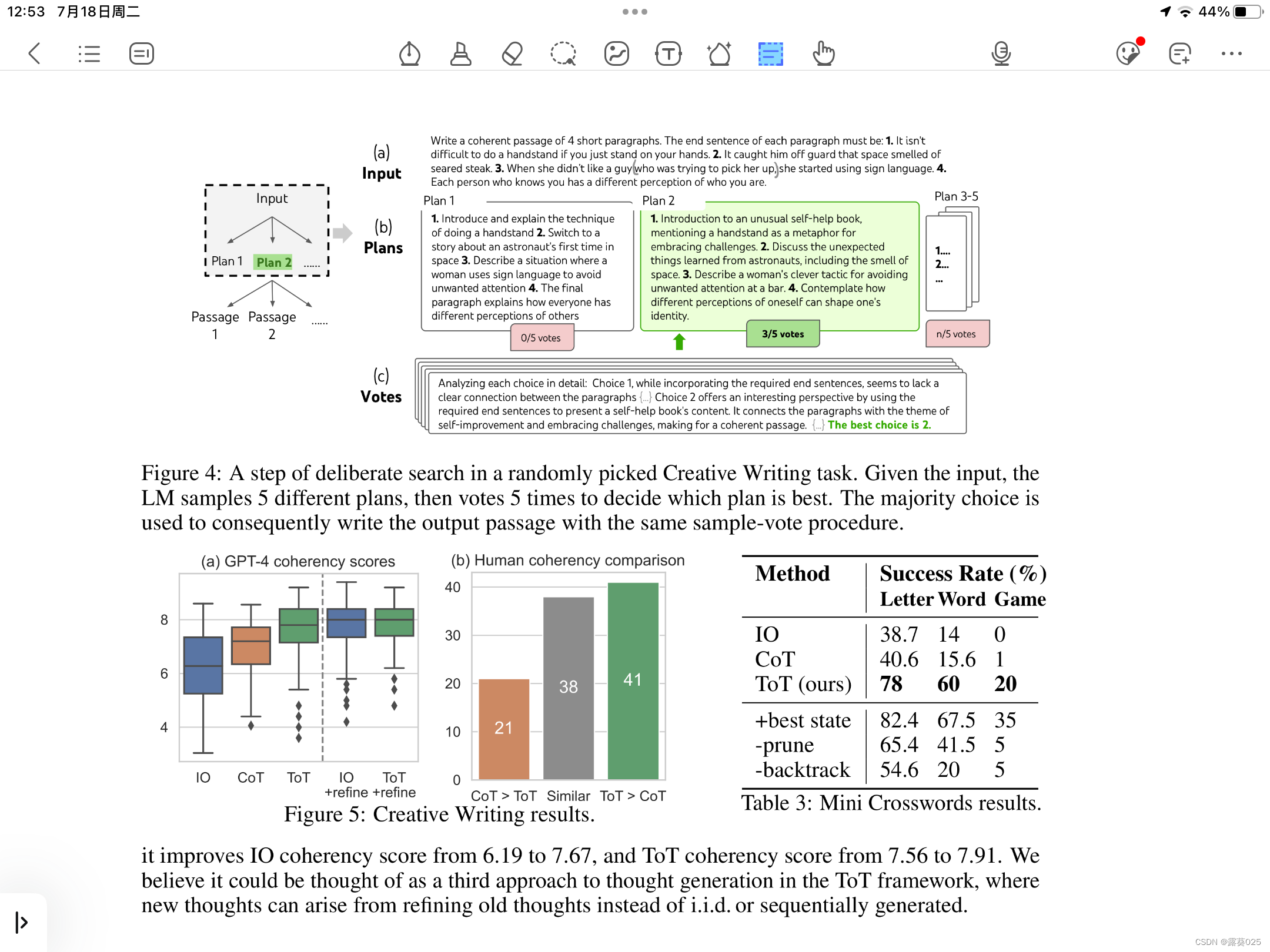
为了开始估算数据所隐含的未来事件,我们进行了初步的风险值估算。首先,所有行的平均值和日期信息的数据框架被转换为时间序列格式,然后从这个时间序列中计算出风险值。根据VaR计算对未来100天和500天的价值进行预测。在随后的预测图中,蓝色圆圈代表未来100天的数值,红色圆圈代表500天的回报值。
plot(ap0$t$Tme\[1:1200\],
alF_ar.d.$fst\[1:1200\])


第 2c 节 - 估计期望_shortfall_(ES),条件VAR_(_CvaR_)_ 10 股票指数
为便于比较,计算了10只股票指数数据的条件风险值(CvaR或估计亏损)。首先,利用数据的时间序列,找到最差的0.95%的跌幅的最大值。然后,通过 "高斯 "方法计算出估计亏损,这两种计算的结果都以表格形式呈现。
ES(s(lD1:2528, 2, rp=FAE\]),p=0.95, mho="gausn")
第 2d 节 - 10 只股票指数的希尔Hill估计
由于假设10股指数数据为重尾分布,数据极少变化,所以采用Hill Estimation对尾指数进行参数估计。目的是验证 10 只股票数据是否为极值分布。Hill Estimation 生成的图证实了。
hil(orvtis, otio="x", trt=15, nd=45)
点击标题查阅往期内容

R语言POT超阈值模型和极值理论EVT分析

左右滑动查看更多

01

02

03

04

第 2e 节 - 正态分布的 Anderson-Darling 检验
Anderson-Darling 检验主要用于分布族,是分布非正态性的决定因素。在样本量较大的情况下(如在 10 股指数中),小于 0.05 的 P 值表明分布与正态性不同。这是极值分布的预期。使用 Anderson-Darling 检验发现的概率值为 3.7^-24,因此证实了非正态性。

第 2f 节 - 结果表
最后,给出了10个股票指数未来价值的估计结果表。3 个 VaR 估计值(和估计差额)的点估计值和范围被制成表格以比较。
VaRES\[3,\] <- c("ES", etFbl\[1\], 4)
eSFbe\[2\], estFtbl\[3\],
rond(eSab\[4\], 4))
第 3a 节 - 10 个股票指数的 EVT 分块最大值估计
极值理论中的 Block Maxima 方法是 EVT 分析的最基本方法。Block Maxima 包括将观察期划分为相同大小的不重叠的时期,并将注意力限制在每个时期的最大观察值上。创建的观察遵循吸引条件的域,近似于极值分布。然后将极值分布的参数统计方法应用于这些观察。
极值理论家开发了广义极值分布。GEV 包含一系列连续概率分布,即 Gumbel、Frechet 和 Weibull 分布(也称为 I、II 和 III 型极值分布)。
在以下 EVT Block Maxima 分析中,10 股指数数据拟合 GEV。绘制得到的分布。创建时间序列图以定位时间轴上的极端事件,从 2006 年到 2016 年。然后创建四个按 Block Maxima 数据顺序排列的图。最后,根据 gev() 函数创建 Block Maxima 分析参数表。
gev(ltMeans, x=0.8, m=0)
plt(alVF)



第 3b 节 - 分块最大值的 VaR 预测
为了从 Block Maxima 数据中创建风险价值 (VaR) 估计,将 10 股指数 GEV 数据转换为时间序列。VaR 估计是根据 GEV 时间序列数据进行的。未来值的预测(未来 100 天和 500 天)是从 VaR 数据推断出来的。在结果图中,蓝色圆圈表示未来 100 天的值,红色圆圈表示 500 天的收益率值。
# 预测未来500天
aGE500<- preit(aG_va.c, n.ad = 500, ci = 0.9)
plot(aGE500pd.500)


第 3c 节 - 分块最大值的期望损失ES (CvaR)
10只股票指数GEV数据的条件风险值("CvaR "或 "期望损失")被计算。首先,利用数据的时间序列,找到最差的0.95%的缩水的最大值。然后,通过极端分布的 "修正 "方法来计算 "估计亏损",这两种计算的结果都以表格形式呈现。
# 条件缩减是最差的0.95%缩减的平均值
ddGV <- xdrow(aEVts\[,2\])
# CvaR(预期亏损)估计值
CvaR(ts(alE), p=0.95, meho="miie")
第 3d 节 - 分块极大值的 Hill 估计
希尔估计(用于尾部指数的参数估计)验证 10 只股票的 GEV 数据是极值分布。
第 3e 节 - 正态分布的 Anderson-Darling 检验
Anderson-Darling 检验是确定大样本数量分布的非正态性的有力决定因素。如果 P 值小于 0.05,则分布与正态性不同。通过该测试发现了一个微小的概率值 3.7^-24。

第 3f 节 - 结果表
最后,给出了对 10 股指数 GEV 未来价值的估计结果表。3 个 GEV VaR 估计值(和 GEV 期望损失)的点估计值和范围制成表格比较。
G_t\[3,\] <- c("GEV ES",sFale\[1\],
sStble\[2\], SEble\[3\],
"NA")
GRst
第 3g 节 - 分块极大值的 100 天 GARCH 预测
通过将 Block Maxima GEV 分布(10 只股票的指数)拟合到 GARCH(1,1)(广义自回归条件异型)模型,对 Block Maxima EVT 数据进行预测。显示预测公式参数表。创建一个“自相关函数”(ACF) 图,显示随时间变化的重要事件。然后,显示拟合模型结果的一组图。创建对未来 20 天(股票指数表现)的预测。最后,20 天的预测显示在 2 个图中。
spec(aanc.ol = list(mel = 'eGARCH',
garer= c(1, 1)),
dirion = 'sd')
# 用广义自回归条件异质性拟合模型
alimol = ugct(pec,allV, sovr = 'ybi')
cofale <- dtafe(cof(litol))
oeBal
plt(l.itodl)




第 4a 节 - 峰值超过阈值估计 - 10 个股票指数
在 EVT 中的峰值超过阈值方法中,选择超过某个高阈值的初始观测值。这些选定观测值的概率分布近似为广义帕累托分布。通过拟合广义帕累托分布来创建最大似然估计 (mle)。MLE 统计数据以表格形式呈现。然后通过 MLE 绘图以图形方式诊断所得估计值。
plot(Dseans, u.rg=c(0.3, 0.35))


第 4b 节 - POT 的 VaR 预测
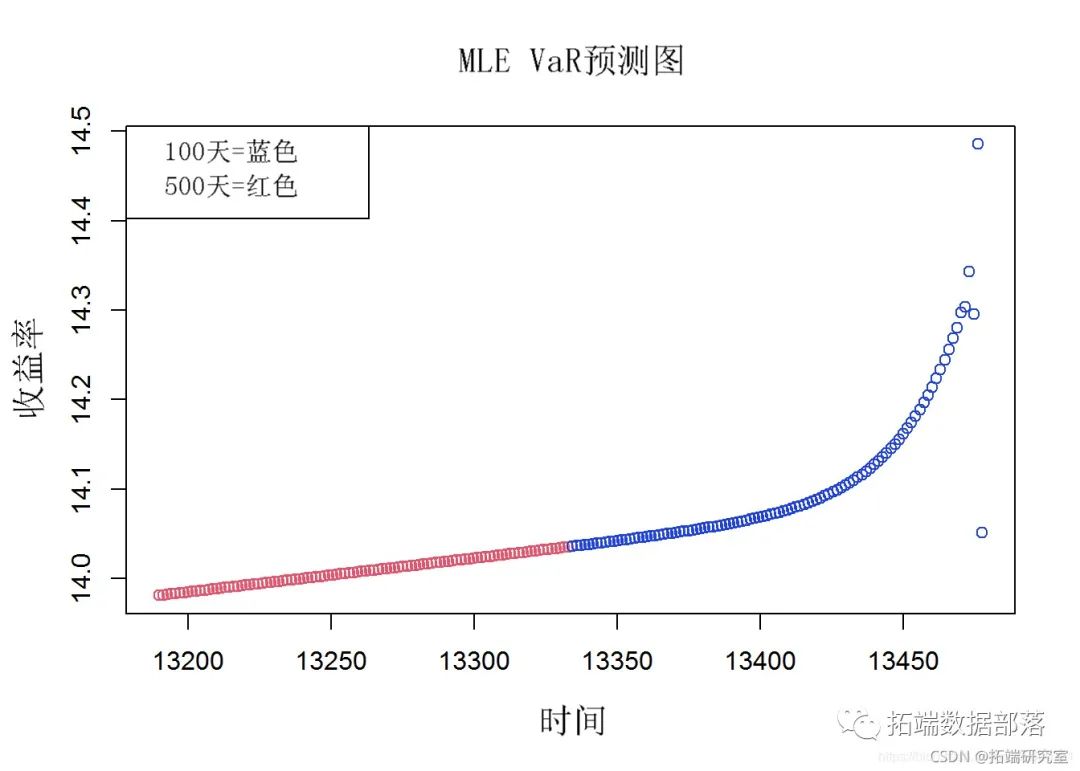
POT 数据的风险价值 (VaR) 估计是通过将 10 个股票指数 MLE 数据转换为时间序列来创建的。VaR 估计是根据 MLE 时间序列数据进行的。未来值的预测(未来 100 天和 500 天)是从 MLE VaR 数据推断出来的。在结果图中,蓝色圆圈表示未来 100 天的值,红色圆圈表示 500 天的收益值。
VAR(merts, p = 2, tp = "cost")
# 预测未来125天、250天和500天
mle_r.pd <- prect(e.ar, n.ahad = 100, ci = 0.9)
plot(mea.prd)
第 4c 节 - POT 的期望损失ES (CvaR) 预测
然后计算10只股票指数MLE数据的条件风险值("CvaR "或 "期望损失ES")。数据的时间序列被用来寻找最差的0.95%的跌幅的最大值。通过极端分布的 "修正 "方法,计算出 "期望损失ES",两种计算的结果都以表格形式呈现。
# 最差的0.95%最大回撤的平均值
mdM <- maxdadw(mlvs\[,2\])
CvaR(ldaa), p=0.95, meto="mdii",
pimeod = "comnen", weghts)
第 4d 节 - 峰值超过阈值的 Hill 估计
Hill 估计(用于尾部指数的参数估计)验证 10 只股票的 MLE 数据是一个极值分布。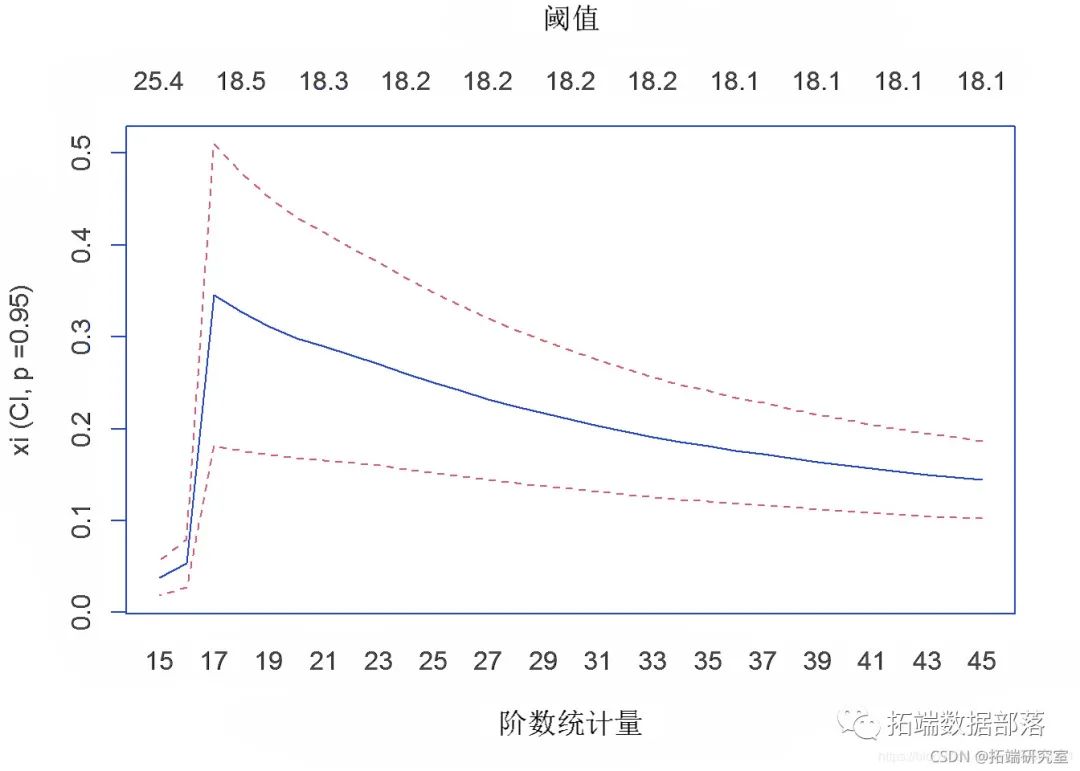
第 4e 节 - 正态分布的 Anderson-Darling 检验
Anderson-Darling 检验是确定大样本数量分布的非正态性的有力决定因素。如果 P 值小于 0.05,则分布与正态性不同。此测试的结果 P 值为 3.7^-24。

第 4f 节 - 结果表
最后,给出了 10 个股票指数 MLE 未来价值的估计结果表。3 个 MLE VaR 估计值(和 MLE 期望损失ES)的点估计值和范围被制成表格来比较。

第 4g 节 - 峰值超过阈值的100天 GARCH 预测
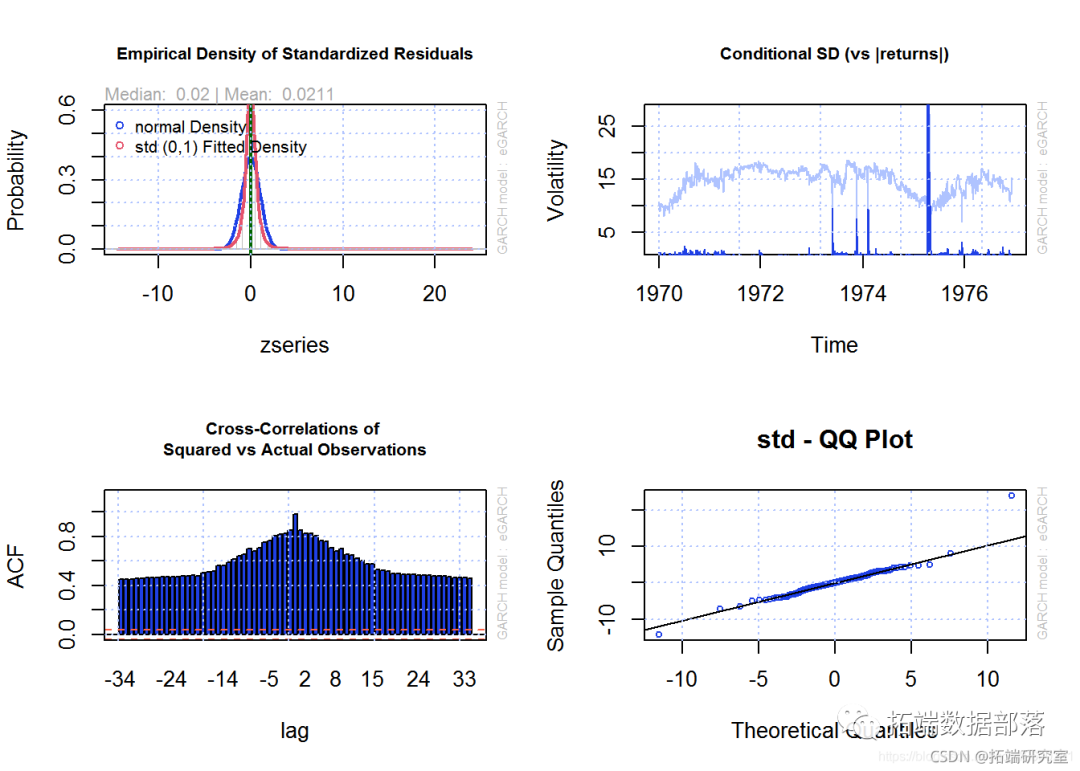
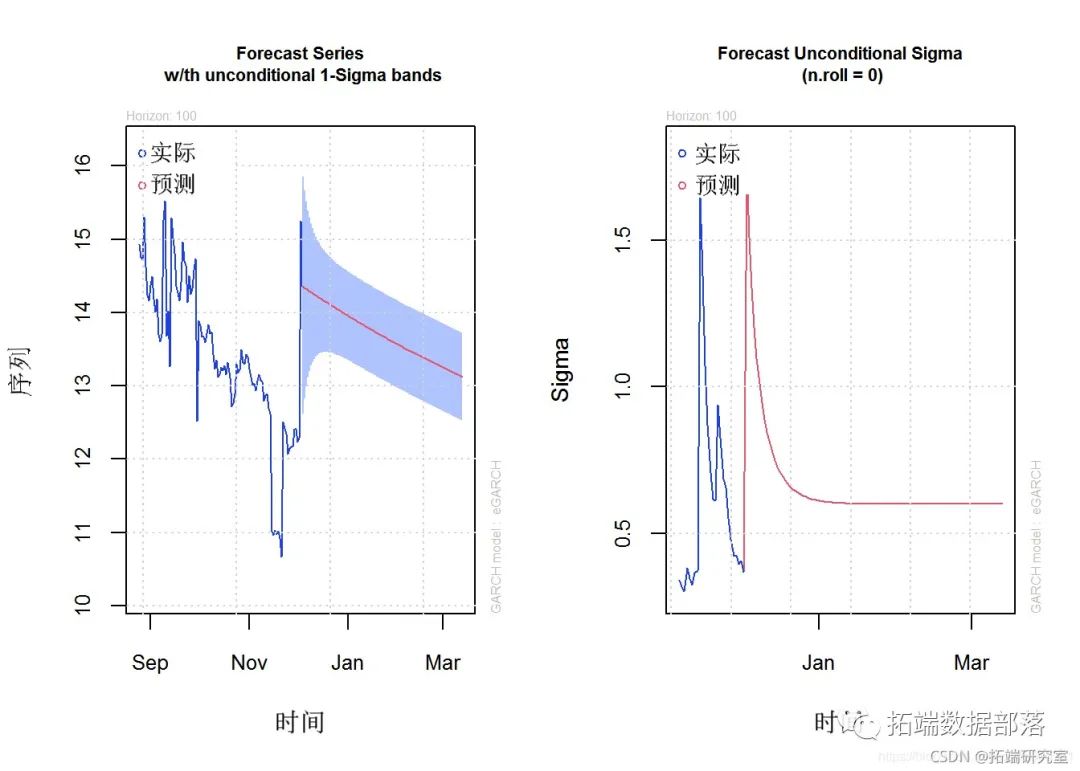
通过将 MLE(10 只股票指数的最大似然估计)拟合到 GARCH(1,1)(广义自回归条件异型性)模型,对峰值超过阈值 EVT 数据进行预测。显示预测公式参数表。创建了一个“自相关函数”(ACF)图,显示了随时间变化的重要事件。然后,显示拟合模型结果的一组图。然后创建对接下来 20 天(股票指数表现)的预测。最后,20 天的预测(来自峰值超过阈值 EVT extimation)显示在 2 个图中。
fit(ec,ta, slvr = 'hybrid')
plot(pot.fite.ol)
第 5a 节 - 估计方法影响表
下表汇总了检验 极值分布的 10 个股票的四种方法的结果。第一列包含四种估计方法的名称。提供了 VaR、ES、mu统计量和 Anderson-Darling P 值的统计量。
c("VaR",
round(mean(cofets),4),
"NA", "NA", p.vau)
c("Block Maxm", round(mean(coffies),4),
MES, pr.ss\[3\],.vle)
c("POT",
round(mean(cofies), 4),
MES, fitdaes, p.ale)
第 5b 节 - 结论
在对10家公司(在证券交易所上市)10年的股票收益率进行检查后,证实了将收益率变化定性为极值分布的有效性。对四种分析方法的拟合值进行的所有安德森-达林测试显示,分布具有正态性或所有非极值的概率不大。这些方法在收益数据的风险值方面是一致的。分块最大值方法产生了一个风险值估计的偏差。传统的VaR估计和POT估计产生相同的风险值。相对于传统的股票收益率数据的CvaR估计,两种EVT方法预测的期望损失较低。标准Q-Q图表明,在10只股票的指数中,Peaks-Over-Threshold是最可靠的估计方法。
本文摘选《R语言极值理论 EVT、POT超阈值、GARCH 模型分析股票指数VaR、条件CVaR:多元化投资组合预测风险测度分析》,点击“阅读原文”获取全文完整资料。


点击标题查阅往期内容
Garch波动率预测的区制转移交易策略
金融时间序列模型ARIMA 和GARCH 在股票市场预测应用
时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格
R语言风险价值:ARIMA,GARCH,Delta-normal法滚动估计VaR(Value at Risk)和回测分析股票数据
R语言GARCH建模常用软件包比较、拟合标准普尔SP 500指数波动率时间序列和预测可视化
Python金融时间序列模型ARIMA 和GARCH 在股票市场预测应用
MATLAB用GARCH模型对股票市场收益率时间序列波动的拟合与预测
R语言GARCH-DCC模型和DCC(MVT)建模估计
Python 用ARIMA、GARCH模型预测分析股票市场收益率时间序列
R语言中的时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格
R语言ARIMA-GARCH波动率模型预测股票市场苹果公司日收益率时间序列
Python使用GARCH,EGARCH,GJR-GARCH模型和蒙特卡洛模拟进行股价预测
R语言时间序列GARCH模型分析股市波动率
R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测
matlab实现MCMC的马尔可夫转换ARMA - GARCH模型估计
Python使用GARCH,EGARCH,GJR-GARCH模型和蒙特卡洛模拟进行股价预测
使用R语言对S&P500股票指数进行ARIMA + GARCH交易策略
R语言用多元ARMA,GARCH ,EWMA, ETS,随机波动率SV模型对金融时间序列数据建模
R语言股票市场指数:ARMA-GARCH模型和对数收益率数据探索性分析
R语言多元Copula GARCH 模型时间序列预测
R语言使用多元AR-GARCH模型衡量市场风险
R语言中的时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格
R语言用Garch模型和回归模型对股票价格分析
GARCH(1,1),MA以及历史模拟法的VaR比较
matlab估计arma garch 条件均值和方差模型
R语言POT超阈值模型和极值理论EVT分析
R语言极值推断:广义帕累托分布GPD使用极大似然估计、轮廓似然估计、Delta法
R语言极值理论EVT:基于GPD模型的火灾损失分布分析
R语言有极值(EVT)依赖结构的马尔可夫链(MC)对洪水极值分析
R语言POT超阈值模型和极值理论EVT分析
R语言混合正态分布极大似然估计和EM算法
R语言多项式线性模型:最大似然估计二次曲线
R语言Wald检验 vs 似然比检验
R语言GARCH-DCC模型和DCC(MVT)建模估计
R语言非参数方法:使用核回归平滑估计和K-NN(K近邻算法)分类预测心脏病数据
matlab实现MCMC的马尔可夫转换ARMA - GARCH模型估计
R语言基于Bootstrap的线性回归预测置信区间估计方法
R语言随机搜索变量选择SSVS估计贝叶斯向量自回归(BVAR)模型
Matlab马尔可夫链蒙特卡罗法(MCMC)估计随机波动率(SV,Stochastic Volatility) 模型
Matlab马尔可夫区制转换动态回归模型估计GDP增长率
R语言极值推断:广义帕累托分布GPD使用极大似然估计、轮廓似然估计、Delta法
欲获取全文文件,请点击左下角“阅读原文”。


![]()