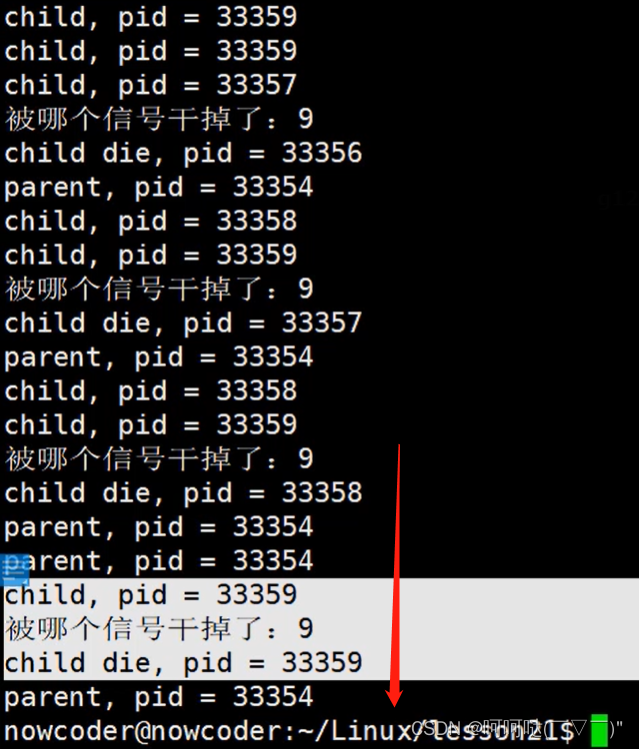
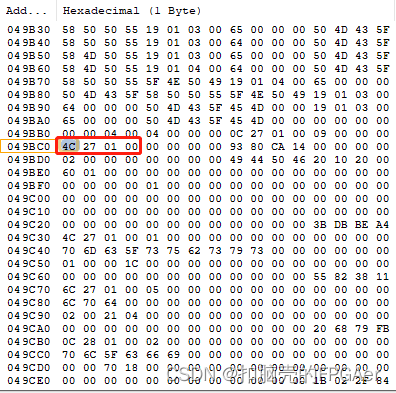
目录
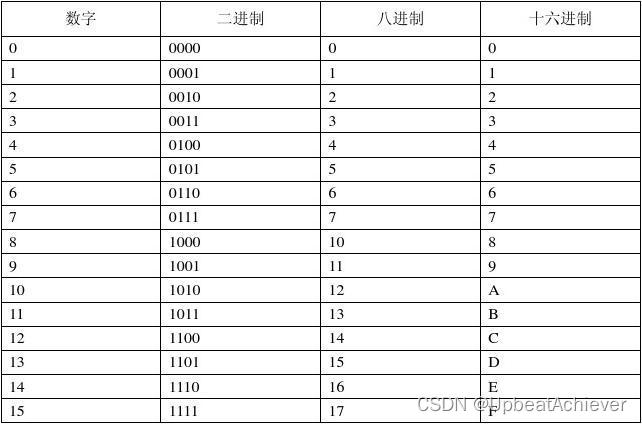
常用进制介绍
十进制
二进制
八进制
十六进制
进制转换
二进制转十进制
十进制转二进制
二进制转十六进制
十六进制转二进制
二进制转八进制
八进制转二进制
十六进制转八进制
八进制转十六进制
常用进制介绍
十进制
介绍:十进制是日常生活中最常用的进位计算制,十进制数中,每一位有0~9十位数字,所以进制为10,低位高位之间“逢十进一”,因此称为十进制。
二进制
介绍:二进制在数字电路、计算机程序等应用中广泛存在,二进制数中,每一位仅有0和1两个数字,所以进制为2。低位高位之间“逢二进一”,因此称为二进制。
八进制
介绍:八进制也存在于某些场合,八进制数中,每一位有0~7八个不同的数字,所以进制为8。低位高位之间“逢八进一”,因此称为八进制。
十六进制
介绍:十六进制的每一位有十六个不同的数码,分别用数字0~9以及用A、B、C、D、E、F分别表示10、11、12、13、14、15。
进制转换
二进制转十进制
二进制转十进制就是将二进制转化为数值大小相等的十进制。
二进制的每一位数从低位到高位分别表示、
、
......
当所在位置为1时,代表该数位存在,用1乘以2对应的次方数,当所在位置为0时,代表该数位不存在,用0乘以2对应的次方数。
以1011这个二进制为例,用十进制表示为
十进制转二进制
十进制转二进制就是将十进制转化为数值大小相等的二进制。
方法是用十进制数连续除以2,将得到的余数逆序排列,即可得到对应的二进制数。
以下图为例:

因此十进制数173对应的二进制数为10101101。图中(173)右下角的10表示十进制数,(10101101)右下角的2表示该数为二进制数。
二进制转十六进制
二进制转十六进制就是将二进制转化为数值大小相等的十六进制。
二进制转十六进制的方法是将二进制按四位四位分开来,因为四位二进制的数转为十进制为15,刚好为十六进制的一个进制周期。
例如1010011110这个二进制数,将其从低位向高位(从右往左)每隔四位区分开来,高位不够四位用0补齐,可以得到 0010 1001 1110。
0010转为十六进制数等于2,
1001转为十六进制数等于9,
1110转为十六进制数等于E,
因此综合起来1010011110这个二进制数转为十六进制数就是29E。
十六进制转二进制
十六进制转二进制就是将十六进制转化为数值大小相等的二进制。
十六进制转二进制就是二进制转十六进制的逆运算,只需要将十六进制数每一位分开来,再将每一位十六进制数转为对应的四位二进制数就可以了。
例如29E这个十六进制数,2转化为二进制为0010,
9转化为二进制数为1001,
E转化为二进制数为1110,
因此29E这个十六进制数转化的二进制数为1010011110。
二进制转八进制
二进制转八进制就是将二进制转化为数值大小相等的八进制。
八进制转二进制的方法是将八进制按三位三位分开来,因为三位二进制的数转为十进制为7,刚好为八进制的一个进制周期,方法和二进制转十六进制类似。
例如10101101这个二进制数,将其从低位向高位(从右往左)每隔三位分开,高位不够用零补齐,可以得到010 101 101。
010这个二进制数对应的八进制数为2,
101这个二进制数对应的八进制数为5,
101这个二进制数对应的八进制数为5,
因此10101101这个二进制数转化的八进制数为255。
八进制转二进制
八进制转二进制就是将八进制转化为数值大小相等的二进制。
八进制转二进制就是二进制转八进制的逆运算,只需要将八进制数每一位分开来,再将每一位八进制数转为对应的三位二进制数就可以了。
例如255这个八进制数,
2这个八进制数对应的二进制数为010,
5这个八进制数对应的二进制数为101,
5这个八进制数对应的二进制数为101,
因此255这个八进制数转化的二进制数为10101101。
十六进制转八进制
十六进制转八进制就是将十六进制转化为数值大小相等的八进制。
方法是先将十六进制转化为数值大小的二进制,再用这个二进制数转化为八进制。
八进制转十六进制
八进制转十六进制就是将八进制转化为数值大小相等的十六进制。
方法是先将八进制转化为数值大小的二进制,再用这个二进制数转化为十六进制。