文章目录
- 作业内容
- 构建视图矩阵(View)
- 构建模型矩阵 (Model)
- 构建透视矩阵(Projection)
- 视口变换(Viewport transform)
- 提高:将三角形绕任意过原点的轴旋转
- 旋转过程中报错
作业内容
本次作业的任务是填写一个旋转矩阵和一个透视投影矩阵。给定三维下三个
点 v0(2.0, 0.0, −2.0), v1(0.0, 2.0, −2.0), v2(−2.0, 0.0, −2.0), 你需要将这三个点的坐
标变换为屏幕坐标并在屏幕上绘制出对应的线框三角形 (在代码框架中,我们已
经提供了 draw_triangle 函数,所以你只需要去构建变换矩阵即可)。简而言之,
我们需要进行模型、视图、投影、视口等变换来将三角形显示在屏幕上。在提供
的代码框架中,我们留下了模型变换和投影变换的部分给你去完成。
需要在main.cpp中修改的函数
// 逐个元素地构建模型变换矩阵并返回该矩阵。在此函数中,你只需要实现三维中绕 z 轴旋转的变换矩阵,
// 而不用处理平移与缩放。
get_model_matrix(float rotation_angle):
//使用给定的参数逐个元素地构建透视投影矩阵并返回该矩阵。
get_projection_matrix(float eye_fov, float aspect_ratio, float zNear, float zFar);
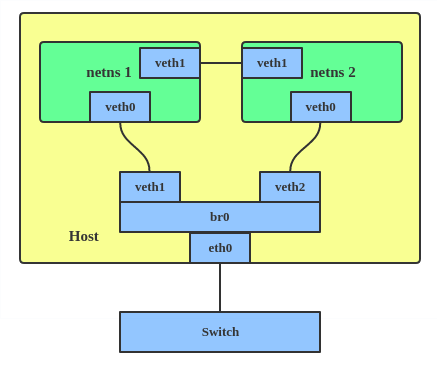
构建视图矩阵(View)
构建模型矩阵 (Model)
这里只需要考虑绕Z轴旋转的矩阵, 绕z轴旋转的矩阵在课程中如下
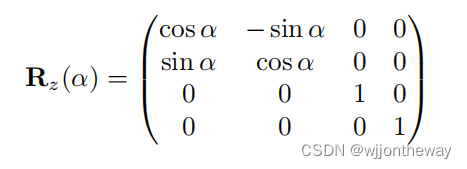
Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
Eigen::Matrix4f model = Eigen::Matrix4f::Identity(); //Unit Matrix
// TODO: Implement this function
// Create the model matrix for rotating the triangle around the Z axis.
// Then return it.
float rotation_angle_radian = rotation_angle * MY_PI / 180.0;
Eigen::Matrix4f rotation_around_z;
float c = cosf(rotation_angle_radian);
float s = sinf(rotation_angle_radian)
rotation_around_z << c, -s, 0, 0,
s, c, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1;
model = model * rotation_around_z;
//std::cout << model << std::endl;
return model;
}
构建透视矩阵(Projection)

计算投影矩阵,需要两步:
-
计算正射投影矩阵
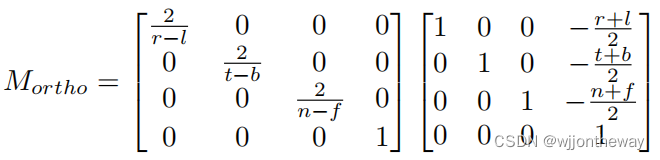
-
计算挤压(squish)矩阵
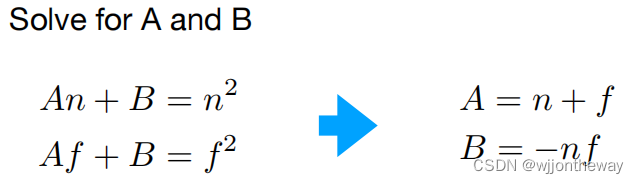
计算挤压矩阵关键就是算A和B
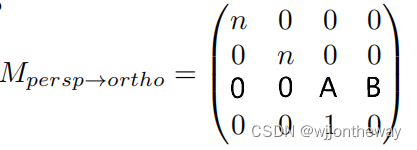
Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
float zNear, float zFar)
{
// Students will implement this function
Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();
// TODO: Implement this function
// Create the projection matrix for the given parameters.
// Then return it.
// Step 1: convert from eye_fov(field of view) and aspect_ration to l, r, b, t
float t = tan((eye_fov*MY_PI/180.0) / 2) * fabs(zNear);
float r = aspect_ratio * t;
float l = -r;
float b = -t;
// Step 2: Create Matrix for Orthographic Projection
// First Create Translate matrix for move center to the origin
Eigen::Matrix4f trans = Eigen::Matrix4f::Identity();
trans(0, 3) = -(r + l) / 2;
trans(1, 3) = -(t + b) / 2;
trans(2, 3) = -(zNear + zFar) / 2;
// Scale to [-1,1]^3
Eigen::Matrix4f scale = Eigen::Matrix4f::Identity();
scale(0, 0) = 2.0 / (r - l);
scale(1, 1) = 2.0 / (t - b);
scale(2, 2) = 2.0 / (zNear - zFar);
// Get Ortho matrix
Eigen::Matrix4f ortho = scale * trans;
//std::cout << "Orthographic:" << std::endl << ortho << std::endl;
Step 3: Create Perspective to Orthographic matrix
float A = zNear + zFar;
float B = -zNear * zFar;
Eigen::Matrix4f pers2ortho;
pers2ortho << zNear, 0, 0, 0,
0, zNear, 0, 0,
0, 0, A, B,
0, 0, 1, 0;
projection = ortho * pers2ortho;
//std::cout << projection << std::endl;
return projection;
}
视口变换(Viewport transform)
Learn OpenGL 坐标系统
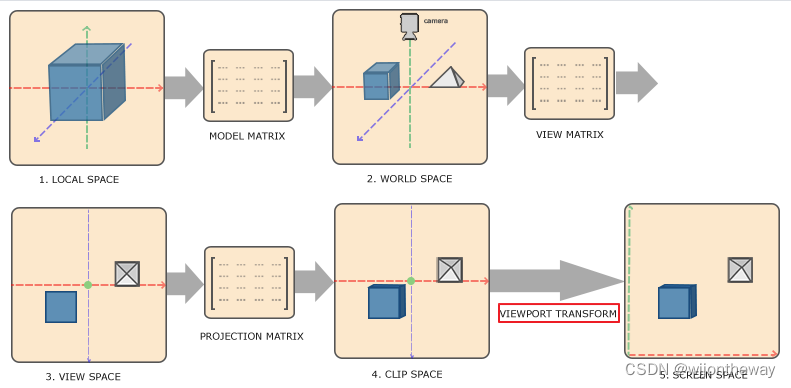
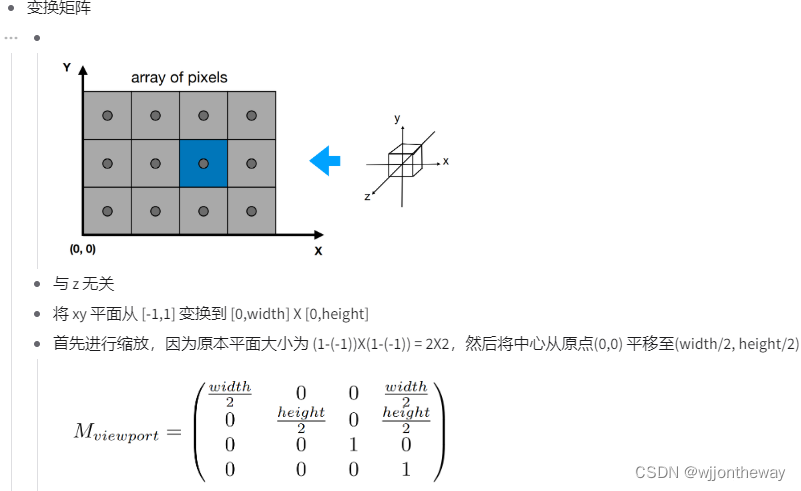
视口变换的部分是在rasterizer::draw接口内做的,视口变化的计算如下:
void rst::rasterizer::draw(rst::pos_buf_id pos_buffer, rst::ind_buf_id ind_buffer, rst::Primitive type)
{
if (type != rst::Primitive::Triangle)
{
throw std::runtime_error("Drawing primitives other than triangle is not implemented yet!");
}
auto& buf = pos_buf[pos_buffer.pos_id];
auto& ind = ind_buf[ind_buffer.ind_id];
float f1 = (100 - 0.1) / 2.0;
float f2 = (100 + 0.1) / 2.0;
Eigen::Matrix4f mvp = projection * view * model;
for (auto& i : ind)
{
Triangle t;
// MVP 变换,并转换为齐次坐标,这一步就是将三角形转换到[1,1]*3的立方体中
Eigen::Vector4f v[] = {
mvp * to_vec4(buf[i[0]], 1.0f),
mvp * to_vec4(buf[i[1]], 1.0f),
mvp * to_vec4(buf[i[2]], 1.0f)
};
// 把w归一化
for (auto& vec : v) {
vec /= vec.w();
}
// 视口变化部分计算
for (auto & vert : v)
{
vert.x() = 0.5*width*(vert.x()+1.0); //width/2*x (Scale) + width/2*1.0
vert.y() = 0.5*height*(vert.y()+1.0); //height/2*x + height/2*1.0
vert.z() = vert.z() * f1 + f2; //对z做的特殊处理
}
for (int i = 0; i < 3; ++i)
{
t.setVertex(i, v[i].head<3>());
t.setVertex(i, v[i].head<3>());
t.setVertex(i, v[i].head<3>());
}
t.setColor(0, 255.0, 0.0, 0.0);
t.setColor(1, 0.0 ,255.0, 0.0);
t.setColor(2, 0.0 , 0.0,255.0);
rasterize_wireframe(t);
}
}
其中一开始对Z的特殊处理不太明白,看到其他博客里面说
可能是因为,近平面设置在0.1,远平面设置在50,用这个式子可以把转移到[-1,1]区间的z值映射到近平面和远平面之间。
参考x和y方向上的操作,实际上z方向也做了scale 和 transport 操作
- 将z方向从[-1,1] 变换到[0.1, 100]
- 将[0,0]平移到透视体的中点
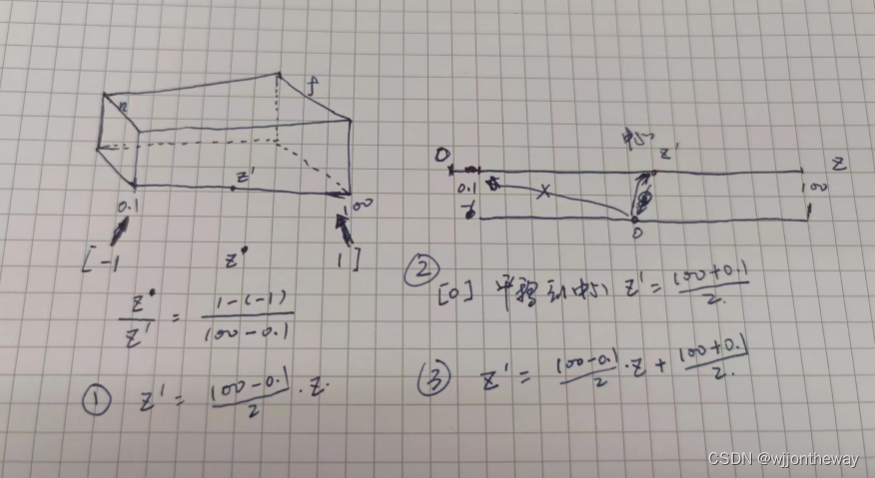
以下就是对z轴的变换做的特殊处理的理解,但是可能不对,是我自己画的示意图。下一节会讲解到Z-buffer,应该会有更好的理解
提高:将三角形绕任意过原点的轴旋转
用到了PPT中的罗德里格斯公式,如何构造一个罗德里格斯公式呢
// converter angle to model matrix
Eigen::Matrix4f get_rotation(Vector3f axis, float angle)
{
float a = angle * PI / 180.0;
// Return for float value
float cosa = cosf(a), sina = sinf(a);
Eigen::Matrix3f I = Eigen::Matrix3f::Identity();
axis = axis.normalized();
// Get N matrix
Eigen::Matrix3f nhat;
nhat << 0, -axis.z(), axis.y(),
axis.z(), 0, -axis.x(),
-axis.y(), axis.x(), 0;
// Rodrigues’ Rotation Formula
Eigen::Matrix3f rodrigues_rotation;
rodrigues_rotation = I + (nhat * nhat) * (1 - cosa) + sina * nhat;
// Contruct to Matrix4f
Eigen::Matrix4f tRet = Eigen::Matrix4f::Zero();
tRet.block<3, 3>(0, 0) = rodrigues_rotation;
tRet.row(3) = Eigen::Vector4f{ 0,0,0,1 };
return tRet;
}
Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
Eigen::Matrix4f model;
// any axis
Vector3f axis{ 1, 1, 0 };
Eigen::Matrix4f t = Eigen::Matrix4f::Identity();
model = get_rotation(axis, rotation_angle);
return model * t;
}
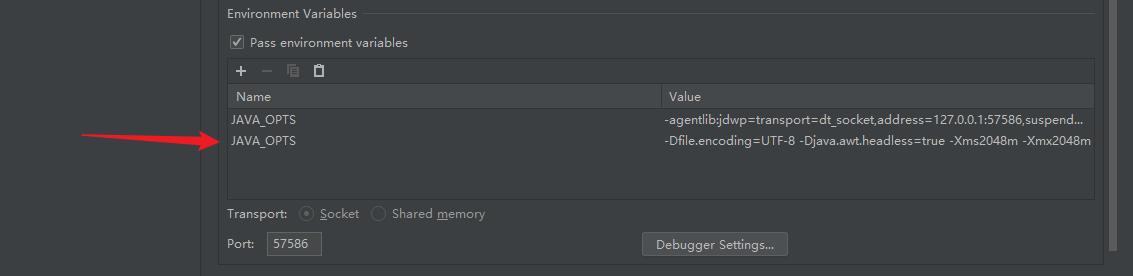
旋转过程中报错
随着按A或者D键旋转三角形,大概旋转了10次左右,程序会崩溃, 报错内容:
expression vector subscript out of range
定位发现是:
void rst::rasterizer::set_pixel(const Eigen::Vector3f& point, const Eigen::Vector3f& color)
{
//old index: auto ind = point.y() + point.x() * width;
if (point.x() < 0 || point.x() >= width ||
point.y() < 0 || point.y() >= height) return;
auto ind = (height-point.y())*width + point.x();
// frame_buf size 为490000, 但是旋转过程中,ind出现大于490000的情况,此时超出了frame_buf的范围,所以会报上述错误
// 额外增加的
if (ind > frame_buf.size())
{
return;
}
frame_buf[ind] = color;
}