全文链接：https://tecdat.cn/?p=33212

本文通过利用回归模型对天猫商品流行度进行了研究，确定了决定天猫商品流行度的重要因素。并讲述、论证了预测天猫商品流行度是天猫商品交易的至关重要的环节。通过对天猫商品流行度预测技术的发展和探讨，深度剖析了天猫商品流行度预测这个研究课题（点击文末“阅读原文”获取完整代码数据）。

相关视频

一、天猫商品流行度预测发展简介

本文使用的数据集为天猫商品数据集（查看文末了解数据免费获取方式）。

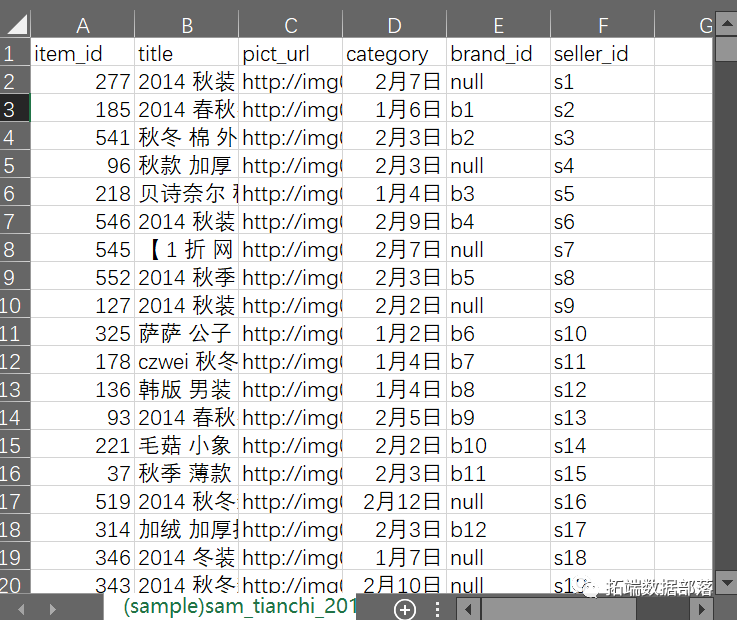
它包含562个商品的属性数据。每个商品包括4个属性，具体的4个属性如下：

该数据集有以下一些变量：

列名	描述
Item_id	[ 1 , 8133507]为整数，表示唯一项(备注:两个以上商家同时提供的 A产品记录在多个不同ID的行中。例如,流行的手机如iPhone 6。)。
Title	一个包含多个关键字的字符串，由' ' 分隔。通过NLP系统从原始标题中提取单词。
Pict_url	在线链接到对应图片的URL 。
Category	字符串' x-y '，其中 ' x '表示其父类，' y '表示其余类。
Brand_id	字符串为' b1 '、' b89366 '，表示商品的品牌。
Seller_id	字符串' s1 '，' s86799 '，表示出售该物品的卖方。

对数据进行概览

summary(data)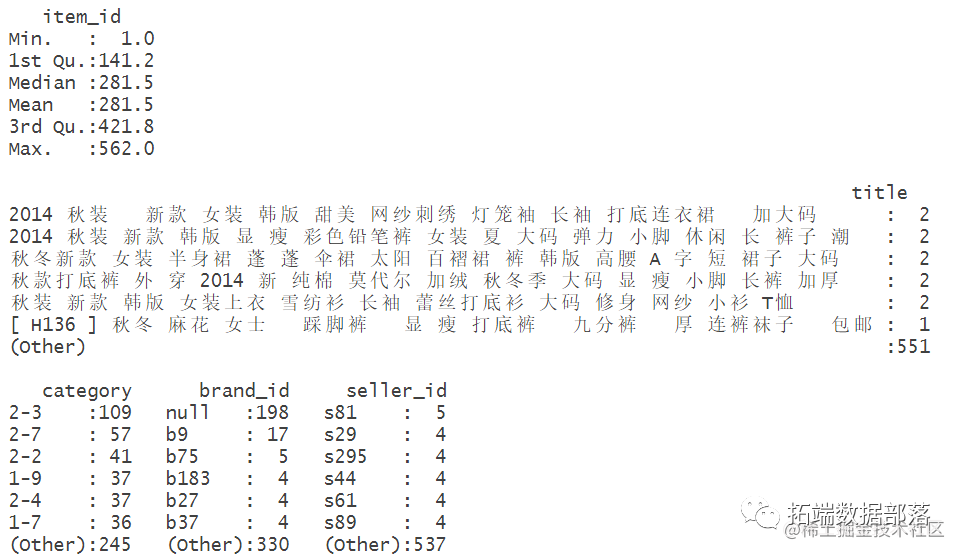

删除缺失值

datanew=na.omit(data)

主要思路

为了准确的估计流行度,了解天猫商品流行度的一般规律,更好为天猫商品投资方提供参考意见,本文从天猫商品流行度和天猫商品相关属性出发,采用多元回归分析方法,建立了线性回归模型,得出了天猫商品流行度变动的影响因素. 具体分析步骤：

1.关系分析

基于以上原理,为大致了解流行度与诸因素之间的关系,先分别绘制流行度与各个因素之间的散点图,并分析它们之间的关系 ,这样可以减少人为因素对流行度的影响,尽量将注意力集中在我们假设选用的自变量上。

2.选择多项式回归模型

2.1变量选取

通过向前向后逐步迭代回归模型筛选出显著性较强的变量进行回归建模。

2.2显著性检验

根据F值和p值统计量来判断模型是否具有显著的统计意义。

2.3拟合预测

使用得到的模型对实际数据进行拟合和预测。

3.拟合不同的模型。查看模型效果，包括对数回归模型，迭代回归模型。

4.分析得出结论

得出各个自变量之间的关系，以及它们对因变量的影响及其意义。

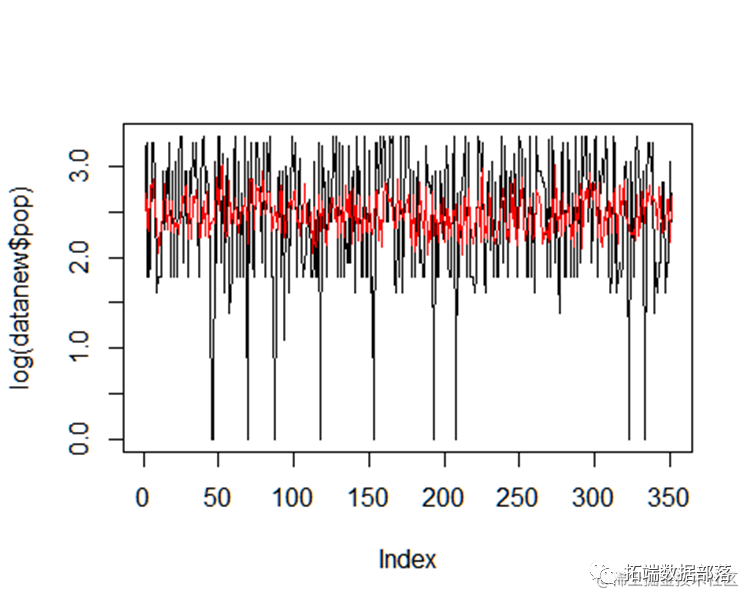
流行度

查看每个类别的出现频率作为流行度，通过直方图查看每个类别出现的频率：

hist(datanew$category)

对每个类别出现的频数的多少进行排序：

order(table(dataneg = T)

datanew$pop=   order(

然后将出现最多的流行度排序为1，然后根据类比的出现频数递增。流行度越大，则出现越少。

建立多元线性：imdb

尝试通过最直观的解释建立模型：

进行多元线性模型并进行分析

设置dummy 变量：从全变量模型可以看出大部分变量无法估计出其参数，说明部分变量不适合用来预测流行度，因此对其中的部分变量进行删减后。得到筛选后的回归模型。

筛选变量

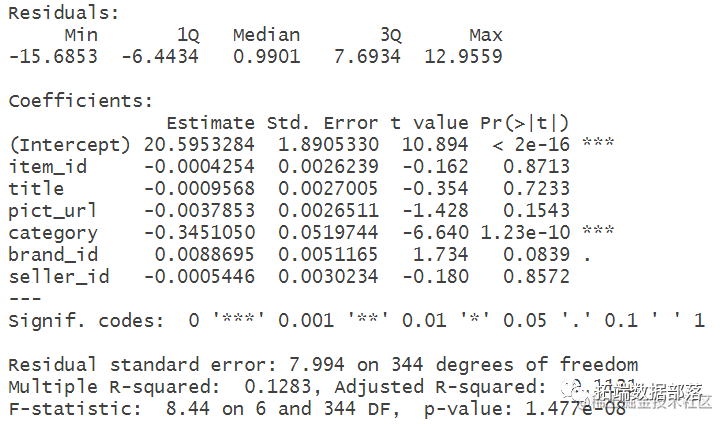
显示回归结果：

点击标题查阅往期内容

贝叶斯线性回归和多元线性回归构建工资预测模型

左右滑动查看更多

模型比较

js
**取对数后的结果**  
summary(lmmod2)显示回归结果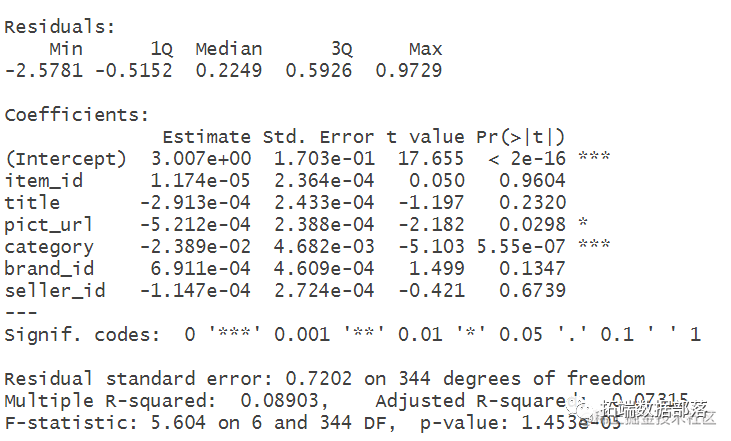

回归结果

plot(datanew$category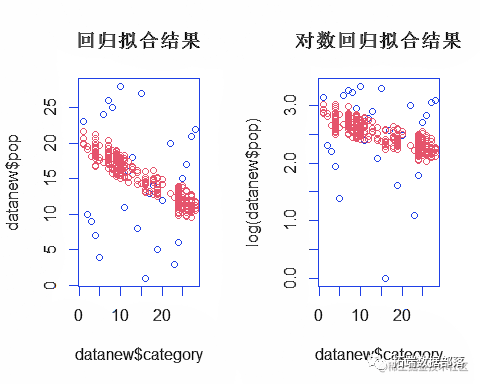

回归结果分析

从输出结果可以看出，流行度和类别和品牌图片地址有显著相关关系，可以看到他们的回归系p数在显著性水平0.05下均显著不为零。进一步地剩余方差的估计值，f统计量的估计值对应的p值< 2.2e-16说明，回归方程是显著的。可决系数R，修正的可决系数R为 0.1左右说明方程的拟合效果一般，还有部分的流行度被其他变量所解释。

回归结果

置信区间与预测区间：

置信区间是给定自变量值后，由回归方程得到的的预测值（实际上是的平均值）的置信区间；预测区间是实际值的置信区间，在这里称为预测区间。预测区间要比置信区间稍大，命令与显示结果如下：

head(predict(lm))

head(predict(lmmod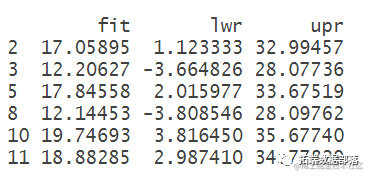

残差分析：

残差分析可以对回归模型的假设条件即随机误差项是否独立同分布进行检验，同时还可以找出离群点。命令语句为plot(lm.1)，显示结果如下

par(mfrow=c(2,2))  
plot(lmmod2)

左上图是拟合值与残差的散点图，从图上可以发现，除去第2个离群点外，所有点基本上是随机地分散在纵坐标值为-1和+1的两条平行线之间，这说明随机误差项具有同方差性；左下图是拟合值与残差的标准差的散点图，其意义与上面类似；右上图表明随机误差项是服从正态分布的，其原因是正态Q-Q图近似地可以看成一条直线；右下图的CooK距离图进一步证实第2个观测值是一个离群点，它对回归方程的影响是比较大的，要根据具体问题，讨论出现这一观测值的实际背景。

点击标题查阅往期内容

数据分享|R语言逐步回归、方差分析anova电影市场调查问卷数据可视化

左右滑动查看更多

逐步回归优化

使用逐步回归法建立“最优”的回归方程

stepmod=step

summary(stepmod)查看模型参数与结果

上面用“逐步向前向后回归法”，通过软件分析建立“最优”回归方程。向后回归法就是建立包含全部因子的回归方程，通过回归系数的检验，从回归方程中逐个剔除不显著的因子，直到留在方程中的因子都是显著的。

总结

从分析结果可以看出，流行度和类别和品牌图片地址有显著相关关系，因此可以认为在天猫购物时，用户会比较关注商品的品牌因素，因为天猫都是正品商铺，购买的用户会比较关注商品的品牌是否为正品等。同时，由于天猫的商品质量有一定的保证，因此用户也会关注该商品的图片，同一个商品可能会因为图片不同而造成不同的流行度。图片好看的商品会有更好的流行度。

数据获取

在公众号后台回复“商品数据”，可免费获取完整数据。