#单调栈：

单调栈就是保持栈内元素有序。和栈与队列（239. 滑动窗口最大值 自己写一个class来实现单调队列）一样，需要我们自己维持顺序，没有现成的容器可以用。

通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，此时我们就要想到可以用单调栈。时间复杂度为O(n)。

单调栈的本质是空间换时间，因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素高的元素，优点是整个数组只需要遍历一次。

#739 每日温度 

用双指针半天写不出。gpt说这种题不能用双指针，得用单调栈。然后用单调栈自己写的：

stack里存的index，遇到更大的就记录，pop原来的，push新的。但是注意，会有不断遇到pop完之后新的top还是比新来的T[i]小，这时候要不断pop，全部pop完之后再 push一次。而不是push多次

vector<int> dailyTemperatures(vector<int>& T) {
       vector<int> res(T.size(),0);
       stack<int> mys;//store the index
       mys.push(0);
       for(int i=1;i<T.size();i++){
           if(T[i]<=T[mys.top()]) mys.push(i);
           else{
                while(!mys.empty() && T[i]>T[mys.top()]){
                    res[mys.top()]=i-mys.top();
                    mys.pop();
                }
                mys.push(i);
            }
       }
       return res;
    }

# 496下一个更大元素I

居然是easy，我不觉得是easy，感觉难度>=#739 每日温度 。太好了，随想录也 “ 看上去和739几乎一样，但是这么绕了一下，其实还上升了一点难度。需要对单调栈使用的更熟练一些，才能顺利的把本题写出来。”

自己写的时候只能想到先像#739那样，把一个弄一个一一对应的vector res把下一个最大的答案存进去，然后再从nums1去nums2里一一对应着找。我自己做的时候最困惑我的一点是：nums1和nums2顺序不同，nums1就很难用

下面是我的AC代码，基于#739的，然后加了一段 O n^2,感觉很慢

vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
        vector<int> res(nums2.size(),-1);
        vector<int> res1(nums1.size(),-1);
        stack<int> mys;//store the index
        mys.push(0);
        for(int i=1;i<nums2.size();i++){
            if(nums2[i]<=nums2[mys.top()]) mys.push(i);
            else{
                    while(!mys.empty() && nums2[i]>nums2[mys.top()]){
                        res[mys.top()]=nums2[i];
                        mys.pop();
                    }
                    mys.push(i);
                }
        }
        for(int i=0;i<nums1.size();i++){
            for(int j=0;j<nums2.size();j++){
                if(nums1[i]==nums2[j]) res1[i]=res[j];
            }
        }
        return res1; 
    }

随想录思路：

对于nums1和nums2找对应： “遍历nums2过程中，要判断nums2[i]是否在nums1（小）中出现过，因为最后是要根据nums1元素的下标来更新result数组。注意题目中说是两个没有重复元素 的数组 nums1 和 nums2。没有重复元素，就可以用map来做映射了。根据数值快速找到下标，还可以判断nums2[i]是否在nums1中出现过。

C++中，当我们要使用集合来解决哈希问题的时候，优先使用unordered_set，因为它的查询和增删效率是最优的。”

改成用unordered map之后快太多了。然后记得if(umap.count(nums2[mys.top()])>0)这个不要忘了，不然不存在的value从umap里获取的idx是0，会出错

vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
        vector<int> res(nums1.size(),-1);
        unordered_map<int,int> umap;
        for(int i=0;i<nums1.size();i++){
            umap[nums1[i]]=i;//key:val, value:idx
        }
    
        stack<int> mys;//store the index
        mys.push(0);
        for(int i=1;i<nums2.size();i++){
            if(nums2[i]<=nums2[mys.top()]) mys.push(i);
            else{
                    while(!mys.empty() && nums2[i]>nums2[mys.top()]){
                        if(umap.count(nums2[mys.top()])>0){
                            int idx_nums1=umap[nums2[mys.top()]];
                            res[idx_nums1]=nums2[i];
                        }
                        mys.pop();
                    }
                    mys.push(i);
                }
        }
        return res; 
    }

# 503下一个更大元素II 变体：circular

自己写的 20min：基础款思路+for(int i=1;i<2*nums.size()-1;i++) for loop多走一次，帮最后一个元素再从头走完； 这种题写的时候要分清是idx还是value，比如我会忘记应该是nums[st.top()]<nums[idx] 而不是直接st.top()<nums[idx]. 随想录和我思路一样。

vector<int> nextGreaterElements(vector<int>& nums) {
        stack<int> st;
        vector<int> res(nums.size(),-1);
        st.push(0);
        for(int i=1;i<2*nums.size()-1;i++){
            int idx=i<nums.size()?i:i-nums.size();
            //int idx=i%nums.size(); also ok
            if(nums[st.top()]>nums[idx]) st.push(idx);
            else{
                while(!st.empty() && nums[st.top()]<nums[idx]){
                    res[st.top()]=nums[idx];
                    st.pop();
                }
                st.push(idx);
            }
        }
        return res;
    }

#42 接雨水 Hard,可多种方法解，面试常考

方法有：双指针法即dp，单调栈法

第一个自己写出的hard！虽然我的ac code跑出来很慢：先求出和前面几个题一样的，右边第一个比自己大的，左边第一个比自己大的，两个vec

然后进一步处理，变成 right里面装 右边最大的（而不是右边第一个最大的），left里面装 从右往左，左边最大的（而不是第一个最大的）

然后left[i]和right[i]取小的那个，做为水的高度，vec[i]就是底的高度。

 int trap(vector<int>& vec) {
        
        vector<int> left(vec.size(),-1);
        vector<int> right(vec.size(),-1);
        stack<int> st;

        //find first right larger
        st.push(0);
        for(int i=1;i<vec.size();i++){
            if(vec[i]<=vec[st.top()]) st.push(i);
            else{
                while(!st.empty() &&  vec[st.top()]<vec[i]){
                    right[st.top()]=vec[i];
                    st.pop();
                }
                st.push(i);
            }
        }

        //get right max
        
        int max=right[right.size()-1];
        for(int i=right.size()-2;i>=0;i--){
            if(right[i]!=-1) {
                max=std::max(max,right[i]);
                right[i]=max;
                //right[i]=std::max(right[i+1],right[i]);

            }
        }
        
        //find first left larger
        while(!st.empty()) st.pop();
        st.push(vec.size()-1);
        for(int i=vec.size()-2;i>=0;i--){
            if(vec[i]<=vec[st.top()]) st.push(i);
            else{
                while(!st.empty() &&  vec[st.top()]<vec[i]){
                    left[st.top()]=vec[i];
                    st.pop();
                }
                st.push(i);
            }
        }
        
        //get left max
        max=left[0];
        for(int i=1;i<left.size();i++){
            if(left[i]!=-1){
                left[i]=std::max(left[i-1],left[i]);
            } 
        }
        
        //cal res
        int sum=0;
        for(int i=0;i<vec.size();i++){
            if(left[i]!=-1 && right[i]!=-1){
                sum+=min(left[i],right[i])-vec[i];
            }
        }
        return sum;
    }

但是！我这个思路太搞笑了，太复杂了，单调栈没用到点上

这样跑起来快多了，思路也正常了。根本不用stack 。这也就是双指针法（这个也是dp方法）

int trap(vector<int>& vec) {
        
        vector<int> left(vec.size(),-1);
        vector<int> right(vec.size(),-1);

        int max_right = 0;
        for(int i = vec.size() - 1; i >= 0; i--) {
            max_right = max(max_right, vec[i]);
            right[i] = max_right;
        }

        int max_left = 0;
        for(int i = 0; i < vec.size(); i++) {
            max_left = max(max_left, vec[i]);
            left[i] = max_left;
        }
        //cal res
        int sum=0;
        for(int i=0;i<vec.size();i++){
            if(left[i]!=-1 && right[i]!=-1){
                sum+=min(left[i],right[i])-vec[i];
            }
        }
        return sum;
    }

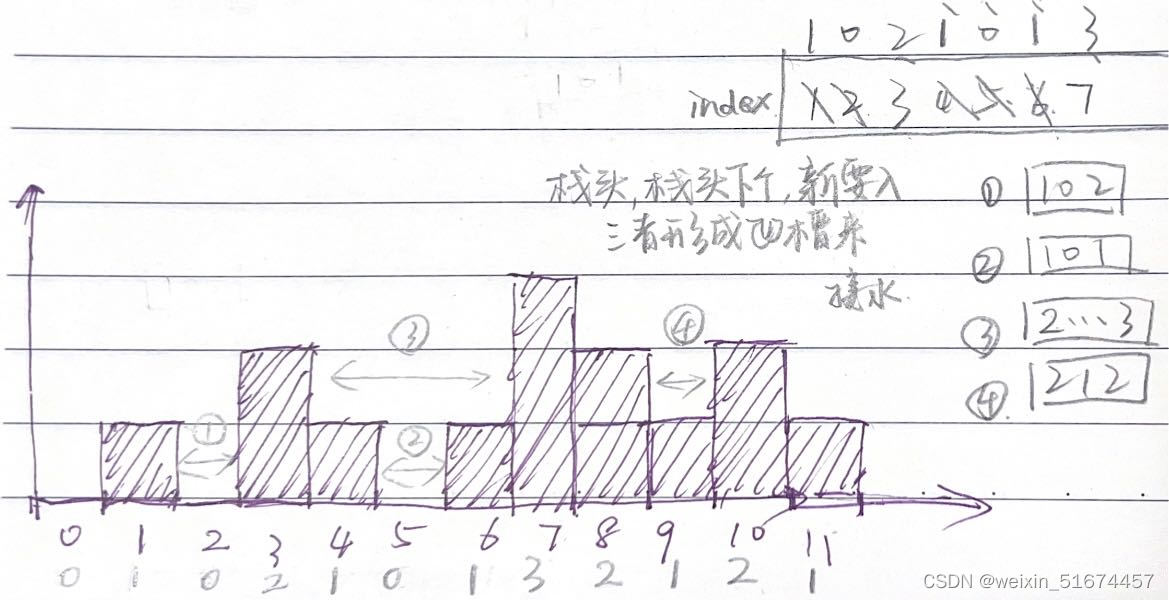
单调栈方法：

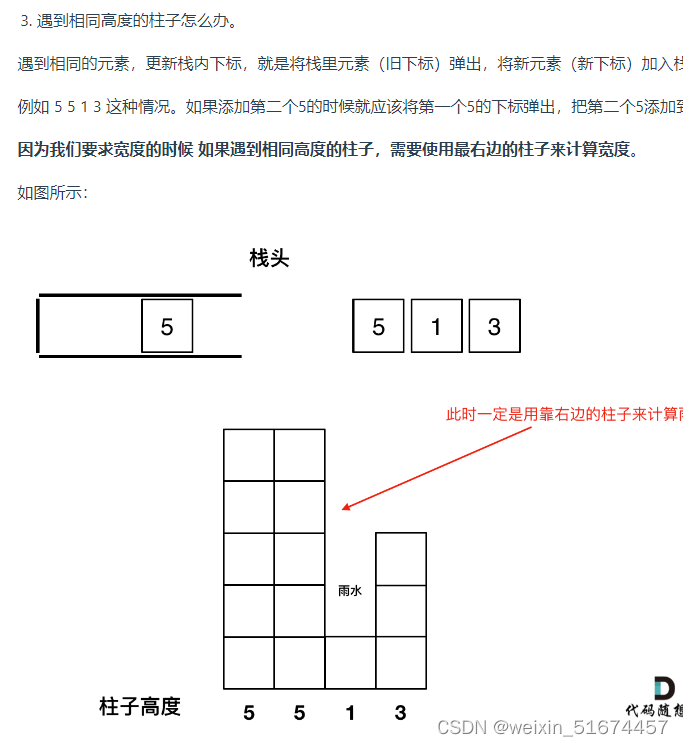
 栈顶和栈顶的下一个元素以及要入栈的元素，三个元素来接水！

 

int trap(vector<int>& height) {
        stack<int> st; 
        st.push(0);
        int sum = 0;
        for (int i = 1; i < height.size(); i++) {
            if (height[i] < height[st.top()]) {     
                st.push(i);
            } if (height[i] == height[st.top()]) { 
                //updatt, so we can use the right most pole
                st.pop(); 
                st.push(i);
            } else {                                
                while (!st.empty() && height[i] > height[st.top()]) { 
                    int mid = st.top();//stack top
                    st.pop();
                    if (!st.empty()) {//stack top next
                        int h = min(height[st.top()], height[i])- height[mid];
                        int w = i - st.top() - 1; 
                        //printf("h: %d, w: %d from %d -%d\n",h,w,i,st.top());
                        sum += h*w;
                    }
                }
                st.push(i);
            }
        }
        return sum;
    }

# 84 柱形图中最大的矩形

想了半天，好难，不会做。本来想用dp做，递推公式想不出来。但是请记住，递推公式发现太麻烦复杂想不出来，也是一种进展！说明我们发现用dp表不合适，要换一种方法了！

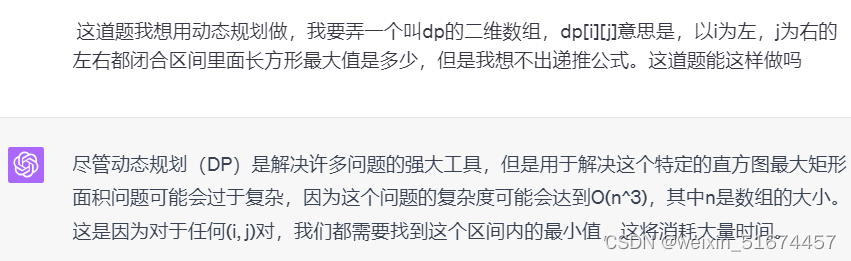
 不懂为什么随想录说是为了防止死循环。

大概思路是图里这样，对每个柱子，相当于找高度和他高度一样的矩形

 

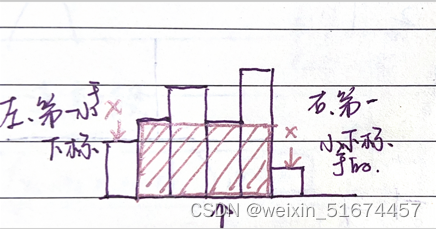
 while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];
            minLeftIndex[i] = t;

这里我觉得好难理解。其实就是现在要找i左边第一个小于他的，左边第一个是t，不满足。接下来我们要找的还是要比i小的，那至少也要比t小，既然t的左边第一个小于的已经找到了，那我们就用他的。但也要重新和t代表的值比一下大小。

 int largestRectangleArea(vector<int>& heights) {
        vector<int> minLeftIndex(heights.size());
        vector<int> minRightIndex(heights.size());
        int size = heights.size();

        // 每柱子 左第一个小于该柱子的下标
        minLeftIndex[0] = -1; // 注意这里初始化，防止下面while死循环
        for (int i = 1; i < size; i++) {
            int t = i - 1;
            while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];
            minLeftIndex[i] = t;
        }
        // 每柱子 右第一个小于该柱子的下标
        minRightIndex[size - 1] = size; // 注意这里初始化，防止下面while死循环
        for (int i = size - 2; i >= 0; i--) {
            int t = i + 1;
            
            while (t < size && heights[t] >= heights[i]) t = minRightIndex[t];
            minRightIndex[i] = t;
        }
    
        int result = 0;
        for (int i = 0; i < size; i++) {
            int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);
            result = max(sum, result);
        }
        return result;
    }