基于多目标优化算法的电力系统分析（Matlab代码实现）

news2025/1/10 23:40:44

💥💥💥💞💞💞欢迎来到本博客❤️❤️❤️💥💥💥
🎉作者研究：🏅🏅🏅主要研究方向是电力系统和智能算法、机器学习和深度学习。目前熟悉python网页爬虫、机器学习、群智能算法、深度学习的相关内容。希望将计算机和电网有效结合！⭐️⭐️⭐️
🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者

📋📋📋本文目录如下：⛳️⛳️⛳️

目录

1 概述

2 数学模型

3 算例及运行结果

4 参考文献

5 结论

6 Matlab代码实现

1 概述

1980 年代和 1990 年代世界多个国家因垄断和寡头垄断模式的结构性失败而经历的能源危机，创造了电力市场自由化的全球趋势，以利用所提供的优势和好处通过竞争模型。在此背景下，发展中国家和发达国家政府对其立法进行了一系列改革，以实施扩大私人投资参与的战略，特别是在发电领域。政府和投资者必须掌握代表发电项目生命周期的成本信息，以及对此类项目的技术和财务评估的稳健指标的分析，其中考虑到某些变量变化的敏感性。高度不确定性，可能会影响项目的成本，从而影响其可行性。这些信息和指标有助于在发电园区的规划阶段做出决策。在学术文献中常用来比较不同类型的通信技术的指标中发电，确定产生 MWh 的成本或分析不同因素在其计算中的作用，有平准化电力成本 (LCOE)，分析发电期间的成本总和发电源的使用寿命除以一段时间内产生的电能总和 [1] [2] [3]。该指标以美元/兆瓦时 [USD/MWh] 表示，可以解释为投资者收回所有运营成本以及资本成本所需的最低收入 [4]。 LCOE 的优势之一是可以用于比较具有不同使用寿命、建设时间、运营成本 (OpEx)、工厂因素、投资成本 (CapEx) 和/或费率折扣（加权平均资本成本 - WACC）根据每个国家的实际情况。事实上，在某些国家，政府支持新的可再生能源技术的政策是基于 LCOE 估计的，并且为了能够对项目进行适当的估值，它们为投资者提供了一些用于计算的输入数据 [5]。

在发电项目财务评估的背景下，电力平准化成本（LCOE）用作比较发电技术的工具；然而，它的一个弱点是它对计算所输入的能量变量存量的敏感性。从这个意义上说，每个作者使用不同的标准和方法进行敏感性分析，其中有：蒙特卡罗方法、马科维茨、CVaR、扩展 Lévy 模型等。在本文中，基于 LCOE 的计算，提出了应用多目标优化技术的敏感性分析。对于定义为与敏感性相关的每个变量，都获得了帕累托前沿。将优化问题模型应用于所提出的研究案例，以对结果进行验证和分析。结果表明，Pareto 前沿方法对于 LCOE 的敏感性分析非常有用，提供了一个很棒的工具。

2 数学模型

$F R C=\frac{r(1+r)^{n}}{(1+r)^{n}-1}=\left(\sum_{t=1}^{n} \frac{1}{(1+r)^{t}}\right)^{-1}$

$V A N=-C a p E x+\sum_{t=1}^{n} \frac{\left(\operatorname{In} g_{t}-O p E x_{t}\right)}{(1+r)^{t}}$

详细数学模型及解释见第四部分。

3 算例及运行结果

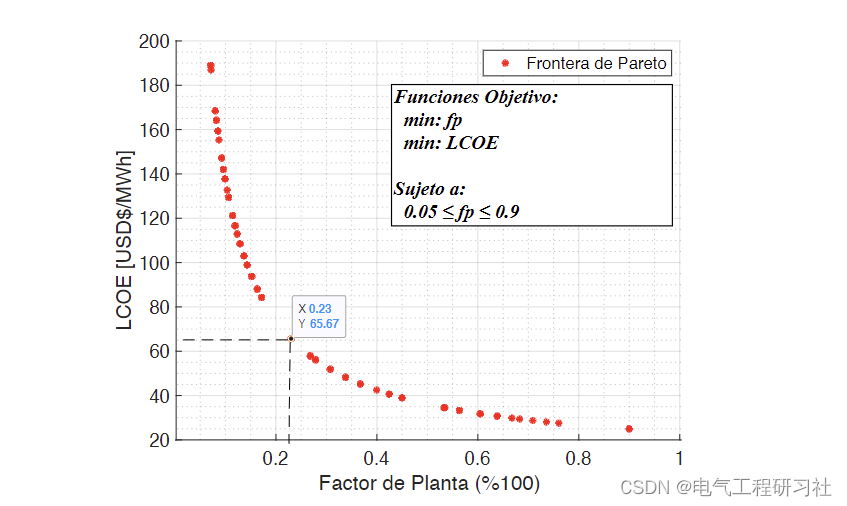
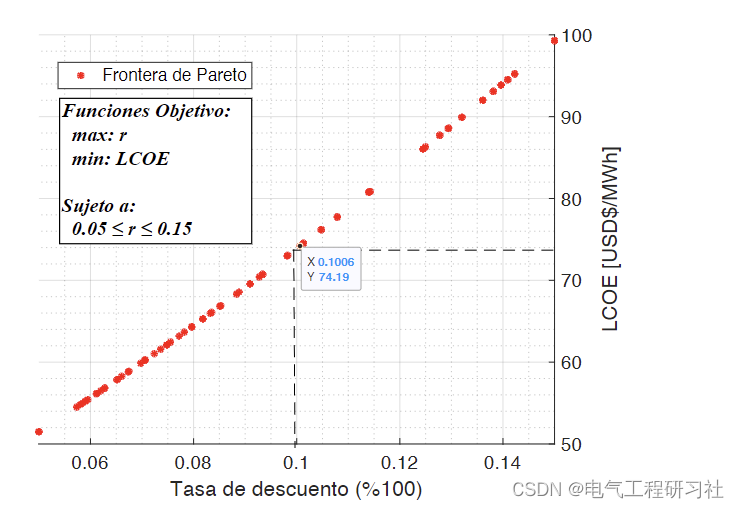
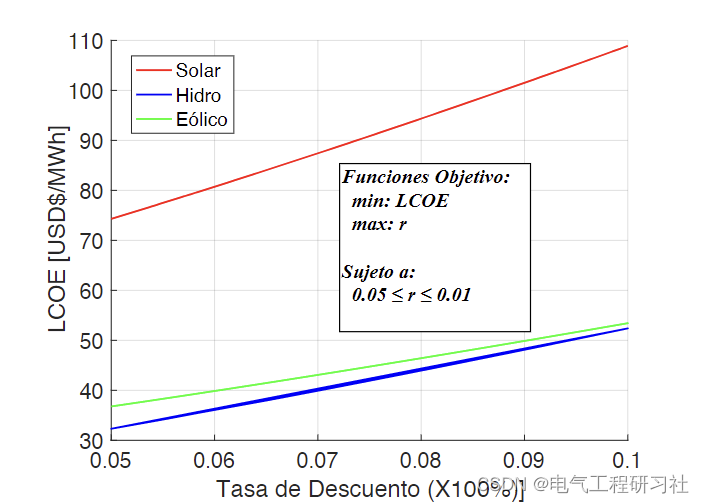
4 参考文献

5 结论

在电厂系数的情况下，对于 0.5 和 0.9 之间的值，LCOE 的敏感性较低，即水电和热电等技术的价格不会因为该参数的变化而发生剧烈变化，不像光伏、风能等技术在管理植物因子低于 0.5 时，其 LCOE 确实会因植物因子的变化而遭受更明显的变化。在发电项目财务评估的背景下，平准化电力成本（平准化成本）被用作比较发电技术的工具;然而，它的弱点之一是它对用于计算的能量变量输入的存量的敏感性。从这个意义上说，每个作者都使用不同的标准和方法来进行敏感性分析，其中包括：蒙特卡洛方法，Markowitz，CVaR，扩展Lévy模型等。本文基于平准化度电成本的计算，提出一种应用多目标优化技术的灵敏度分析方法。帕累托前沿是针对定义为与灵敏度相关的每个变量获得的。将优化问题模型应用于所提研究案例，用于结果的验证和分析。