1.算法描述

OFDM是 Orthogonal Frequency Division MulTIplexing的缩写，即正交频分复用，是一种无线环境下的高速传输技术，也可以看作一种特殊的FDM形式。OFDM 技术的主要思想就是在频域内将给定信道分成许多正交子信道，在每个子信道上使用一个子载波进行调制，并且各子载波并行传输。

　　对于移动通信，其信道的频率响应曲线大多是非平坦的，具有频率选择性，但是每个子信道而言又是相对平坦的，在每个子信道上进行的是窄带传输，信号带宽小于信道的相应带宽，因此就可以大大消除信号波形间的干扰。由于这种技术具有在杂波干扰下传送信号的能力，因此常常会被利用在容易外界干扰或者抵抗外界千扰能力较差的传输介质中。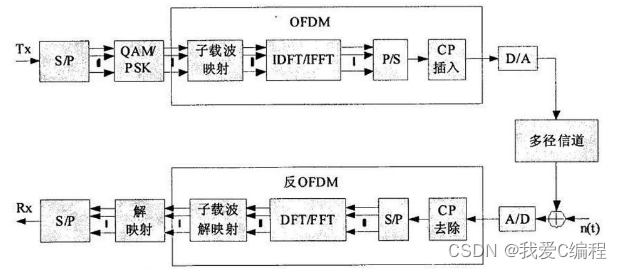

OFDM中的各个载波是相互正交的，每个载波在一个符号时间内有整数个载波周期，每个载波的频谱零点和相邻载波的零点重叠，这样便减小了载波间的干扰。由于载波间有部分重叠，所以它比传统的FDMA提高了频带利用率。

　　在OFDM传播过程中，高速信息数据流通过串并变换，分配到速率相对较低的若干子信道中传输，每个子信道中的符号周期相对增加，这样可减少因无线信道多径时延扩展所产生的时间弥散性对系统造成的码间干扰。另外，由于引入保护间隔，在保护间隔大于最大多径时延扩展的情况下，可以最大限度地消除多径带来的符号间干扰。如果用循环前缀作为保护间隔，还可避免多径带来的信道间干扰。在过去的频分复用（FDM）系统中，整个带宽分成N个子频带，子频带之间不重叠，为了避免子频带间相互干扰，频带间通常加保护带宽，但这会使频谱利用率下降。为了克服这个缺点，OFDM采用N个重叠的子频带，子频带间正交，因而在接收端无需分离频谱就可将信号接收下来。

　　OFDM系统的一个主要优点是正交的子载波可以利用快速傅利叶变换（FFT/IFFT）实现调制和解调。对于N点的IFFT运算，需要实施N^2次复数乘法，而采用常见的基于2的IFFT算法，其复数乘法仅为（N/2）log2N，可显著降低运算复杂度。

　　在OFDM系统的发射端加入保护间隔，主要是为了消除多径所造成的ISI。其方法是在OFDM符号保护间隔内填入循环前缀，以保证在FFT周期内OFDM符号的时延副本内包含的波形周期个数也是整数。这样时延小于保护间隔的信号就不会在解调过程中产生ISI。由于OFDM技术有较强的抗ISI能力以及高频谱效率，2001年开始应用于光通信中，相当多的研究表明了该技术在光通信中的可行性。

但是，OFDM技术区分各个子信道的方法是利用各个子载波之间严格的正交性。频偏和相位噪声会使各个子载波之间的正交特性恶化，仅仅1％的频偏就会使信噪比下降30dB。因此，OFDM系统对频偏和相位噪声比较敏感。

交频分复用 (OFDM)是4G通信中的关健技术之一,主要依靠各子载波之间的正交性实现高速传输.但OFDM对载波频偏(CFO,Carrier Frequency Offset)非常敏感,很小的频偏就会引起信道间的干扰(ICI).从理论上分析了载波频偏产生信道间干扰的过程,重点研究了CFO对OFDM性能的影响,并对相关结论进行了仿真验证.

发射机的载波Ftx和接收机的载波Frx，是由各自射频硬件电路上的晶振源提供，由于是两个独立的物理器件，不可避免的存在频率上的偏差。频率偏差，会造成调制数据相位上的旋转，在接收端必须对频偏进行纠正。
介绍了OFDM调制的本质，是两级的IQ调制，第二级IQ调制，将第一级得到的复信号，实部和虚部分别在I路和Q路上发射出去。基带的IQ两路序列为x(n)的实部和虚部：

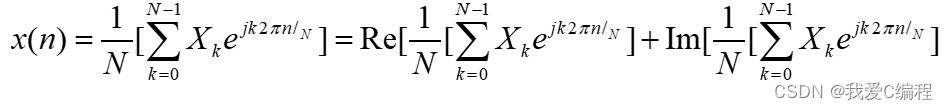
为方便表达，通常将第二级IQ调制发射出去的射频信号表达为复等效形式：

Ftx为发射载波频率，相当于把基带的x(n)信号，搬到Ftx频点上发射出去。在接收端，采用与Ftx相同的载波频率将x(n)搬到基带，于是有

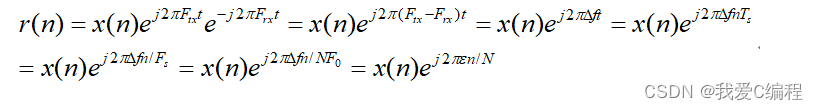
正交频分复用(OFDM)以及它和多输入多输出(MIMO)的结合—MIMO-OFDM是目前宽带无线通信非常具有潜力的传输技术之一,然而,OFDM和MIMO-OFDM技术对载波频偏(CFO)和相位噪声(PHN)非常敏感,CFO和PHN会破坏OFDM子载波的正交性,严重恶化系统性能。因此,有效对抗CFO和PHN成为OFDM和MIMO-OFDM技术实现的一个重要挑战。

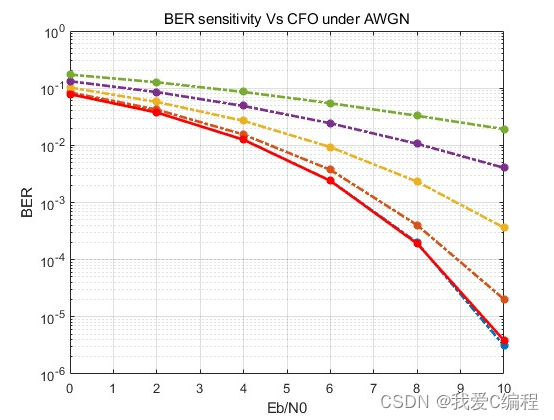
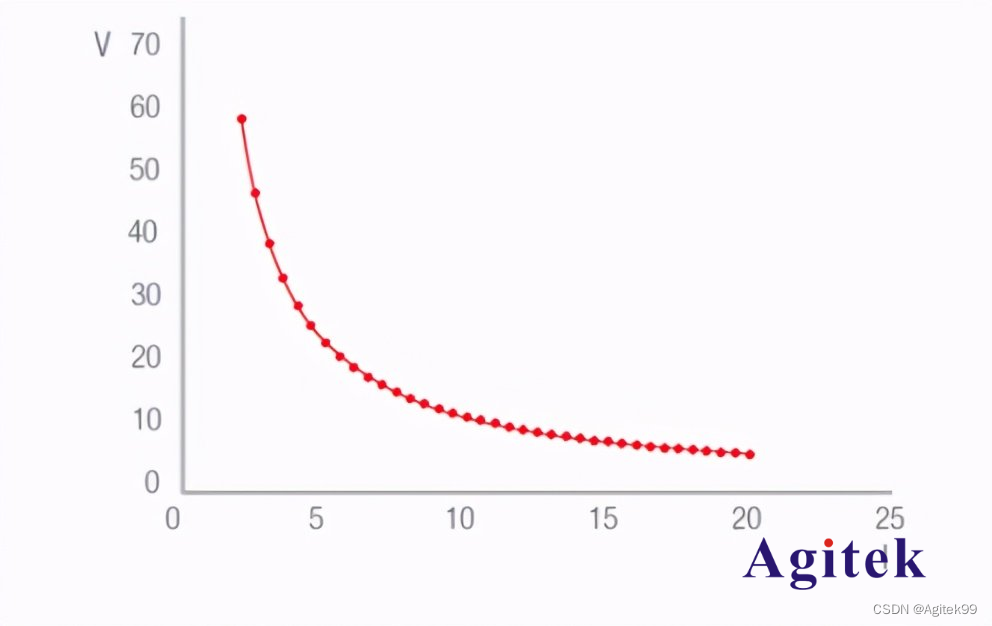
2.仿真效果预览

matlab2022a仿真结果如下：

3.MATLAB核心程序

for ii = 1:length(CFO)
    
    for n = 1:length(EbN0dB)
        snr = EbN0dB(n);
        berrors = 0;tic;
        for mc = 1:MC
            x = rand(1,nDSC)>0.5;
            xt = 2*x -1; 
            xt = (nFFT/sqrt(nDSC))*ifft(fftshift(xt),nFFT); 
            xtt = [xt(end-nCP+1:end) xt];
            % Gaussian noise of unit variance, 0 mean
            nt = 1/sqrt(2)*(randn(1,nTot) + 1i*randn(1,nTot));
            yr = sqrt(nTot/nFFT)*xtt + 10^(-EsN0dB(n)/20)*nt;
            % applying CFO
            yr =(exp(1i*2*pi*CFO(ii)*(0:length(yr)-1)/nFFT)).*yr;
            % Receiver processing
            yr = yr(nCP+1:end);
            yr = (nDSC/sqrt(nFFT))*fftshift(fft(yr,nFFT));
            yr = yr > 0; % hard demodulation
            berrors = berrors + length(find((yr-x)~=0));
        end
        toc;
       BER(ii,n) = berrors/(nFFT*MC);
    end
    
end
A_102