[基因遗传算法]进阶之三:实践CVRP

实践CVRP

参考资料:《实现VRP常见求解算法——遗传算法（GA）》
属于该篇文章的解读

文章目录

- 实践CVRP
- - A. 定义三个class
  - B.读取数据,打造初始属性卡
  - C. 路线规划
  - D. 生成解的初始空间(初代种群)
  - D. 计算每个路段route的距离
  - E. 计算适应度
  - F.物竞天择
  - F.交叉
  - G.变异
  - H. 输出的相关函数
  - - a.绘制目标函数收敛曲线
    - b.绘制优化车辆路径
    - c.输出优化结果至xlsx
  - I. 主函数的运行

CVRP问题的解为一组满足需求节点需求的多个车辆的路径集合。假设某物理网络中共有10个顾客节点，编号为1~10，一个车辆基地，编号为0，在满足车辆容量约束与顾客节点需求约束的条件下，此问题的一个可行解可表示为：[0-1-2-0,0-3-4-5-0,0-6-7-8-0,0-9-10-0]，即需要4个车辆来提供服务，车辆的行驶路线分别为0-1-2-0,0-3-4-5-0,0-6-7-8-0,0-9-10-0。由于车辆的容量固定，基地固定，因此可以将上述问题的解先表示为[1-2-3-4-5-6-7-8-9-10]的有序序列，然后根据车辆的容量约束，对序列进行切割得到若干车辆的行驶路线。因此可以将CVRP问题转换为TSP问题进行求解，得到TSP问题的优化解后再考虑车辆容量约束进行路径切割，得到CVRP问题的解。这样的处理方式可能会影响CVRP问题解的质量，但简化了问题的求解难度。

A. 定义三个class

Sol()类 :解集, 存放解的一些相关属性.
Node()类,节点集,存放节点的一些相关属性.—属性卡
Model()类, 将Sol()和Node()加入其中.并且定义了许多 (基因遗传)算法的方法和属性.

好处在于文件夹分类的作用,坏处在于代码水平低的容易报错.为了方便学习,我们保留了Node()和Sol()类.拆分了Model()类. 接下来该顺序运行代码.

# 1.定义Node和Sol类
# 数据结构：解
class Sol():
    def __init__(self):
        self.nodes_seq=None # 解的编码
        self.obj=None # 目标函数
        self.fit=None  # 适应度
        self.routes=None # 解的解码
# 数据结构：网络节点
class Node():
    def __init__(self):
        self.id=0 # 节点id
        self.name=''  # 节点名称，可选
        self.seq_no=0 # 节点映射id
        self.x_coord=0 # 节点平面横坐标
        self.y_coord=0  # 节点平面纵坐标
        self.demand=0 # 节点需求

B.读取数据,打造初始属性卡

xlsx的每行为节点的属性,重点包括有name,id,x_coord,y_coord,demand等.
读取文件后,为每行(every node)打造属性卡,即Node()类. 并将所有的属性卡放入model的卡包,即model.node_list .
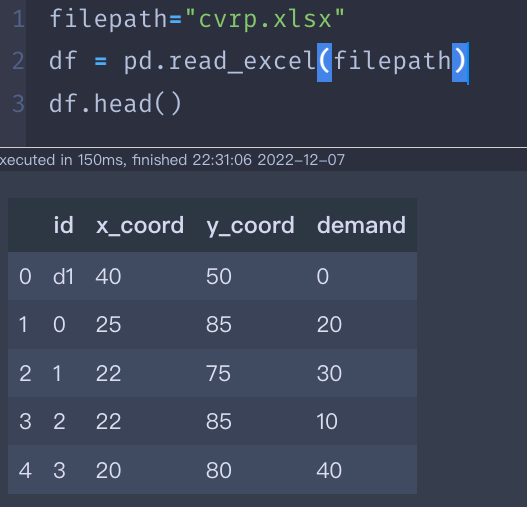
在这里插入图片描述

# 2. 读取xlsx数据,并制作node属性卡片集
filepath="cvrp.xlsx"
df = pd.read_excel(filepath)#col:id	x_coord	y_coord	demand
node_seq_no =-1 #车辆基地的seq_no值为-1,剩余需求节点的seq_no 依次编号为 0,1,2,...
node_list=[]
#这些节点包括两个部分:需求节点+仓库
for i in range(df.shape[0]):
    node=Node()#实例化一个node,并建立属性,最终放入一个列表
    node.id=node_seq_no
    node.seq_no=node_seq_no
    node.x_coord= df['x_coord'][i]
    node.y_coord= df['y_coord'][i]
    node.demand=df['demand'][i]
    if df['demand'][i]==0:
        depot=node #该节点是仓库
    else:
        node_list.append(node)#该节点是需求节点
    # 尝试将节点的name和id号添加到属性中.
    try:
        node.name=df['name'][i]
    except:
        pass
    try:
        node.id=df['id'][i]
    except:
        pass
    node_seq_no=node_seq_no+1 #映射ID号渐增    
number_of_nodes=len(node_list)#需求节点的个数

包装为函数后

# 2. 读取xlsx数据,并制作node属性卡片集
# 2. 读取xlsx数据,并制作node属性卡片集
def readXlsxFile(filepath):
#     filepath="cvrp.xlsx"
    df = pd.read_excel(filepath)#col:id	x_coord	y_coord	demand
    node_seq_no =-1 #车辆基地的seq_no值为-1,剩余需求节点的seq_no 依次编号为 0,1,2,...
    node_list=[]
    node_seq_no_list=[]
    #这些节点包括两个部分:需求节点+仓库
    for i in range(df.shape[0]):
        node=Node()#实例化一个node,并建立属性,最终放入一个列表
        node.id=node_seq_no
        node.seq_no=node_seq_no
        node.x_coord= df['x_coord'][i]
        node.y_coord= df['y_coord'][i]
        node.demand=df['demand'][i]
        if df['demand'][i]==0:
            depot=node #该节点是仓库
        else:
            node_list.append(node)#该节点是需求节点
            node_seq_no_list.append(node_seq_no)
        # 尝试将节点的name和id号添加到属性中.
        try:
            node.name=df['name'][i]
        except:
            pass
        try:
            node.id=df['id'][i]
        except:
            pass
        node_seq_no=node_seq_no+1 #映射ID号渐增    
    return depot,node_list,node_seq_no_list

尝试运行:
在这里插入图片描述

C. 路线规划

在这里实践的问题: 可以看成送快递的问题.有1个仓库, 及N=100个节点需要配送某些物品. 快递员需要使用最小的距离完成配送任务.
目标函数: 路线的的距离最小值
约束条件

每个站点只能去一次,不存在重复节点
运送车vehicle的容量有限vehicle_cap=80,尽可能的多装物品
快递员从depot 出发, 物品配送完后者不支持下一个节点的配送的时候,返回depot

问题理解:

存在快递员一车不能到达所有站点的情况,因此需要快递员多次配送或者多个快递员一块配送.
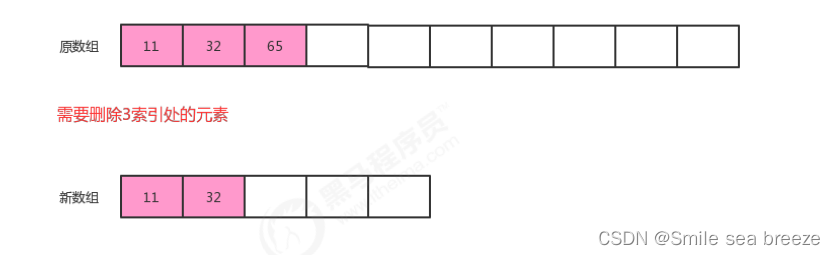
因此会存在多段的路径route,每段都以depot隔开.如下图所示
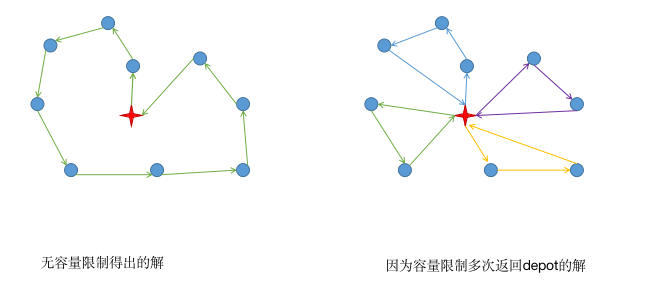
可以看到当选择一条序列路线的时候,会因为capaticy的限制,返回depot.该函数可以如下定义为

# 因为有车的容量的限制.所以,当车无法工作的时候需要返回depot
# 因此,在需要返回仓库的站点后,添加仓库站点
# 3. 车辆容量限制,返回仓库.所以要切割路线
def splitRoutes(nodes_seq,vehicle_cap):
    """
    采用简单的分割方法：按顺序依次检查路径的容量约束，在超出车辆容量限制的位置插入车场。
    例如某TSP解为：[1,2,3,4,5,6,7,8,9,10],
    累计需求为：[10,20,30,40,50,60,70,80,90,10]，
    车辆容量为：30，则应在3,6,9节点后插入车场，
    即得到：[0,1,2,3,0,4,5,6,0,7,8,9,0,10,0]
    """
    # nodes_seq的序列列表,vehicle_cap是车辆的容量限制
    num_vehicle = 0 #记录完成该规划需要用到的车辆.
    vehicle_routes = []#车的新路线
    route = []
    remained_cap = vehicle_cap#80 车的剩余物品总数
    for node_no in nodes_seq:
        # nodes_seq是node的ID顺序列表
        # 判断next node是否可能完成需求任务.     
        if remained_cap - node_list[node_no].demand >= 0:
            ## 任务成功条件: `vehicle内的物品剩余数`-`demand from next node`>=0:
            ## if 成功,则将next node放入本条route中,并车库容量变化  
            route.append(node_no)
            remained_cap = remained_cap - node_list[node_no].demand
        else:
             ## else, 马上开启新一条路.先把route放入总轨迹vehicle_routes
             ##.      再将next node 放入新的一条路route并作为起点.
            vehicle_routes.append(route)
            route = [node_no]
            ## 车的数量加1.车的容量重新恢复到80(回depot过了),并执行next node的任务
            num_vehicle = num_vehicle + 1
            remained_cap =vehicle_cap - node_list[node_no].demand
    vehicle_routes.append(route) #将循环的最后一个route加入
    return num_vehicle,vehicle_routes

做个测试
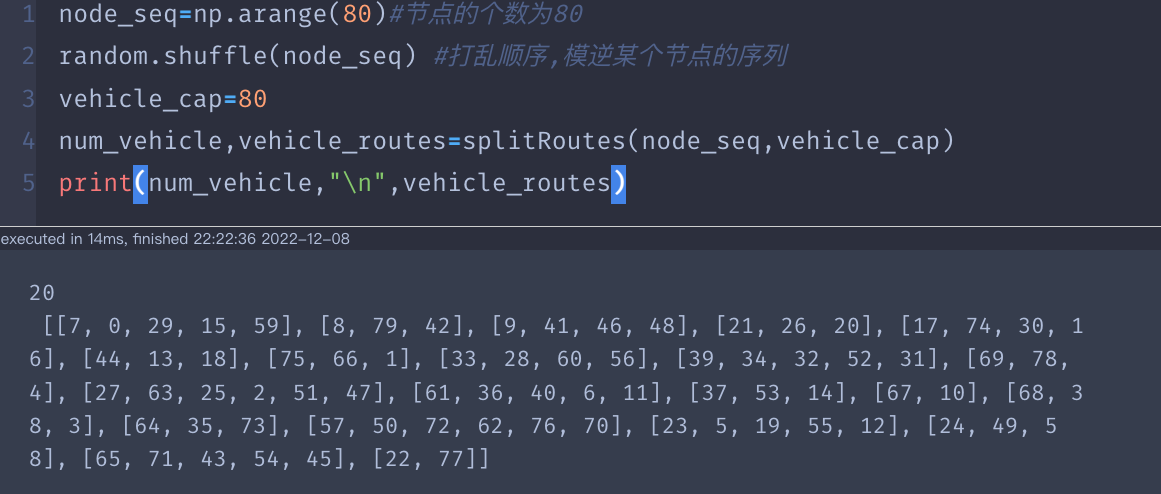
在这里插入图片描述

D. 生成解的初始空间(初代种群)

sol需要满足约束, 且具有自己的属性. 对于每个解并进行路线切割.

# 4. 构造初始解
def genInitialSol(popsize):
    sol_list=[]#用于存放种群
    nodes_seq=np.arange(number_of_nodes)# 种群的ID号集合,从0,1,2,..
    # 生成100个初始种群
    for i in range(popsize):
        # 使用随机种子,并打乱序列
        random.seed(random.randint(0,10))
        random.shuffle(nodes_seq)
        # 实例化一个Sol,并添加ID序列
        sol=Sol()
        sol.nodes_seq=copy.deepcopy(nodes_seq)#使用深复制,避免指针指向同一个索引
        # 将单个sol(个体)放入列表(种群)
        sol_list.append(sol)
    return sol_list    
sol_list=genInitialSol(100)

D. 计算每个路段route的距离

计算两个节点之间的距离
计算从depot出发回到depot的路线距离

def Distance(u,v,dis="Eur"):
    # u,v是node(),计算两个节点之间的距离
    if dis=="Eur":
        ## 欧式距离
        dis=math.sqrt((u.x_coord-v.x_coord)**2+(u.y_coord-v.y_coord)**2)
    else:
        ##如果是经纬度坐标
        dis=geodesic((u.x_coord,u.y_coord),(v.x_coord,v.y_coord)).m
        #长度路径单位为米
    return dis 
def calDistance(route):
    # route为路线:为节点的ID号或索引号
    # depot为仓库节点
    distance=0 # 初始为0,距离累加
    for i in range(len(route)-1):
        # n个节点,共有n-1个路段
        from_node=node_list[route[i]] #每个路段的起点
        to_node= node_list[route[i+1]]#每个路段的重点
        distance += Distance(from_node,to_node) #累计长度
    ## 添加起点和终点分别与depot的距离
    distance += Distance(depot,node_list[route[0]])
    distance += Distance(node_list[route[-1]],depot)
    return distance

做个小测试:
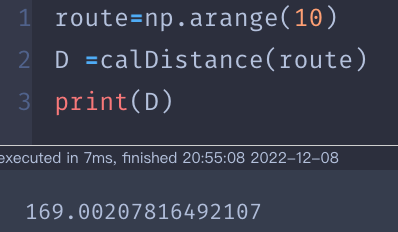
在这里插入图片描述

E. 计算适应度

车辆的总轨迹包括多个路段route.要求总轨迹较小.

# 6. 计算适应度

def calFit(sol_list):
    # sol_list解集,种群集合
    #calculate fit value：fit=Objmax-obj
    Objmax=-float('inf')#最优解的目标值,初始为极小值负无穷
    best_sol=Sol()#record the local best solution记录最优物种
    best_sol.obj=float('inf') #初始最优解的目标函数值为正无穷
    for sol in sol_list:
        nodes_seq=sol.nodes_seq
        num_vehicle, vehicle_routes = splitRoutes(nodes_seq, vehicle_cap)
        ##优化目标设为求路径的最短距离
        distance=0 #初始距离,累计求和
        for route in vehicle_routes:
            distance+=calDistance(route)
        sol.obj=distance#解的优化目标值
        sol.routes=vehicle_routes#解,车的总轨迹
        ## 优化目标值,并更新
        if sol.obj>Objmax:
            Objmax=sol.obj
        if sol.obj < best_sol.obj:
            best_sol = copy.deepcopy(sol)
    ##计算种群的适应度calculate fit value
    for sol in sol_list:
        sol.fit=Objmax-sol.obj
    #update the global best solution
    if best_sol.obj<best_sol.obj:
        best_sol=best_sol
    return best_sol,sol_list

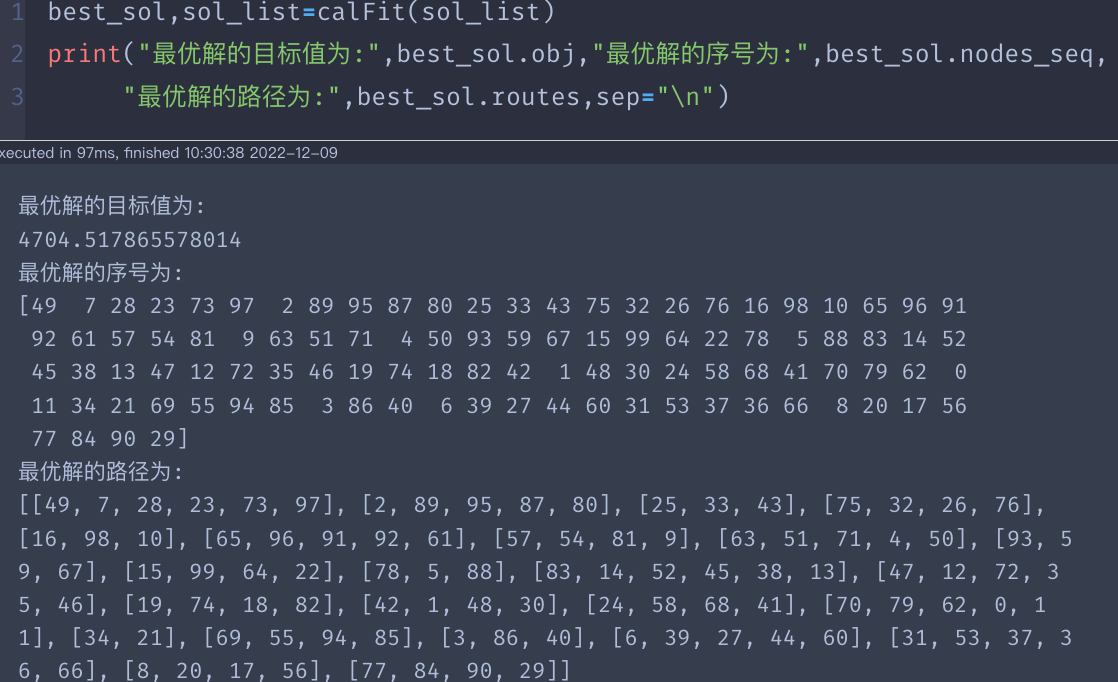
做测试:计算出sol_list中每个解sol的属性有:obj(目标值),routes(解的分割),fit(解的适应度)
并记录当下的最优解:best_sol
在这里插入图片描述

F.物竞天择

# 7.  二元锦标赛(物竞天择)
def selectSol(sol_list):
    # 物竞天择,旧种群根据适应度的赌命运获得新的一代种群
    # 这里赌命运的方式:随机选择两个个体pk适应度,适应度大者保留.从而筛选获得新一代种群
#     sol_list=copy.deepcopy(model.sol_list)
    sol_list_new=[]  
    for i in range(len(sol_list)):
        f1_index=random.randint(0,len(sol_list)-1)#随机选手1
        f2_index=random.randint(0,len(sol_list)-1)#随机选手2
        f1_fit=sol_list[f1_index].fit#计算选手1的适应度
        f2_fit=sol_list[f2_index].fit
        if f1_fit<f2_fit:
            sol_list_new.append(sol_list[f2_index])
        else:
            sol_list_new.append(sol_list[f1_index])
    return sol_list_new

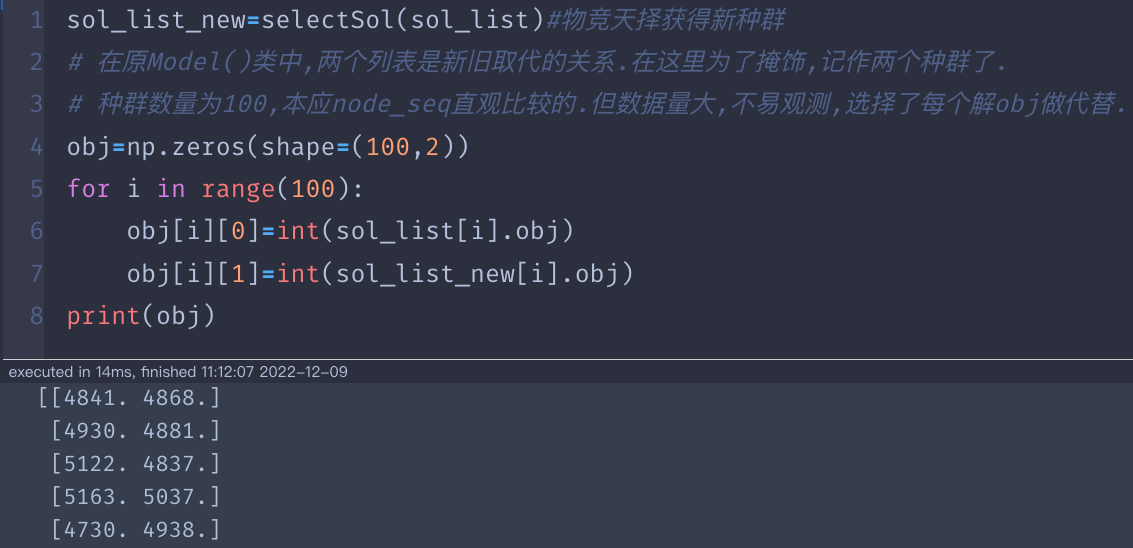
做个测试:这里区分了新旧两代种群,是为了展示.而实际的应用中种群是取代关系即.
sol_list=selectSol(sol_list)
在这里插入图片描述

F.交叉

根据基因遗传算法, 前面的种群筛选,只能在纯种之间,如果想要获得更多结果,则需要交叉和变异.
如何交叉,突变,原理?
在这里插入图片描述

情况一:对图中绿色部分交叉的时候,如何做?
在对应的交叉部分有4个数字,只有0和1是公共数字. 将f2中的3和6置换到f1中的时候,f1则会重复出现两次3和6,而缺少9和8. 因此,我们需要对非交叉部分的3和6替换到9和8,从而节点的只访达一次的约束.
情况二:对途中的绿色部分不交叉而是保留,其他部分进行交叉.好处是交叉的次数由3次变为2次.
方法: 根据交绿色部分索引, 我们将其划分为3部分.

f1分割为:new_c1_f, new_c1_m(保留), new_c1_b
f2 分割为:new_c2_f, new_c2_m(保留), new_c2_b

☀️Step1: 对于f2中的节点去判断是否属于f1中的保留部分new_c1_m, 获得new_c1_f和new_c1_b

 for index in range(number_of_nodes):
     if len(new_c1_f)<cro1_index:
         if f2.nodes_seq[index] not in new_c1_m:
             new_c1_f.append(f2.nodes_seq[index])
     else:
         if f2.nodes_seq[index] not in new_c1_m:
             new_c1_b.append(f2.nodes_seq[index])

如果 new_c1_f的内容没有填满,即len(new_c1_f)<cro1_index.修改:< 变为<=

如果f2中的节点f2.nodes_seq[index]不在f1的交叉序列中,则将该节点放入new_c1_f中

如果new_c1_f的内容已经填满,即else

如果f2中的节点f2.nodes_seq[index]不在f1的交叉序列中,则将该节点放入new_c1_b中

☀️Step2: 对于f1中的节点去判断是否属于f2中的保留部分new_c2_m, 获得new_c2_f和new_c2_b.原理同上.

# 8.OX交叉
def crossSol(sol_list,number_of_nodes):
    """
    sol_list:种群 
    number_of_nodes:需求节点的个数 
    """
    popsize=100#种群数量
    pc=0.6 #交叉概率
    sol_list_new=[]#用于存放新的种群
    while True:
        #随机选择两个parent的ID号
        f1_index = random.randint(0, len(sol_list) - 1)#parent1
        f2_index = random.randint(0, len(sol_list) - 1)#parent2
        #如果两个parent不同,则交叉.相同跳过重新选择.
        if f1_index!=f2_index:
            f1 = copy.deepcopy(sol_list[f1_index])
            f2 = copy.deepcopy(sol_list[f2_index])
            if random.random() <= pc:
                # 交叉概率
                #将解划分为3个部分,中间部分保留.其他的交叉.
                cro1_index=int(random.randint(0,number_of_nodes-1))
                cro2_index=int(random.randint(cro1_index,number_of_nodes-1))
                new_c1_f = []
                new_c1_m=f1.nodes_seq[cro1_index:cro2_index+1]#sol1筛选部分索引
                new_c1_b = []
                new_c2_f = []
                new_c2_m=f2.nodes_seq[cro1_index:cro2_index+1]#sol2筛选部分索引
                new_c2_b = []
                for index in range(number_of_nodes):
                    if len(new_c1_f)<cro1_index:
                        if f2.nodes_seq[index] not in new_c1_m:
                            new_c1_f.append(f2.nodes_seq[index])
                    else:
                        if f2.nodes_seq[index] not in new_c1_m:
                            new_c1_b.append(f2.nodes_seq[index])
                for index in range(number_of_nodes):
                    if len(new_c2_f)<cro1_index:
                        if f1.nodes_seq[index] not in new_c2_m:
                            new_c2_f.append(f1.nodes_seq[index])
                    else:
                        if f1.nodes_seq[index] not in new_c2_m:
                            new_c2_b.append(f1.nodes_seq[index])
                new_c1=copy.deepcopy(new_c1_f)
                new_c1.extend(new_c1_m)
                new_c1.extend(new_c1_b)
                f1.nodes_seq=new_c1#交叉后的解f1的映射ID序列
                new_c2=copy.deepcopy(new_c2_f)
                new_c2.extend(new_c2_m)
                new_c2.extend(new_c2_b)
                f2.nodes_seq=new_c2#交叉后的解f2的映射ID序列
                sol_list_new.append(copy.deepcopy(f1))#将新解放入新种群
                sol_list_new.append(copy.deepcopy(f2))
            else:
                sol_list_new.append(copy.deepcopy(f1))#不交叉时,将解放入新种群
                sol_list_new.append(copy.deepcopy(f2))
            if len(sol_list_new)>popsize:
                # 如果新解的数量大于种群数量,停止交叉
                break
    return sol_list_new

运行一下
在这里插入图片描述

G.变异

原理在于, 对于任意一个解(sol,个体), 其映射ID的序列,任意选择两个交换位置.

# 9.变异
def muSol(sol_list,number_of_node):
#     sol_list=copy.deepcopy(model.sol_list)
    sol_list_new=[]# 用于存放变异后的新种群
    pm=0.2 #突变概率
    popsize=100#种群数量
    while True:
        f1_index = int(random.randint(0, len(sol_list) - 1))
        f1 = copy.deepcopy(sol_list[f1_index])# 在种群中随机选择一个 个体
        m1_index=random.randint(0,number_of_nodes-1)
        m2_index=random.randint(0,number_of_nodes-1)
        if m1_index!=m2_index:
            if random.random() <= pm:
                node1=f1.nodes_seq[m1_index]
                f1.nodes_seq[m1_index]=f1.nodes_seq[m2_index]
                f1.nodes_seq[m2_index]=node1
                sol_list_new.append(copy.deepcopy(f1))
            else:
                sol_list_new.append(copy.deepcopy(f1))
            if len(sol_list_new)>popsize:
                break
    return sol_list_new

运行一下
在这里插入图片描述

H. 输出的相关函数

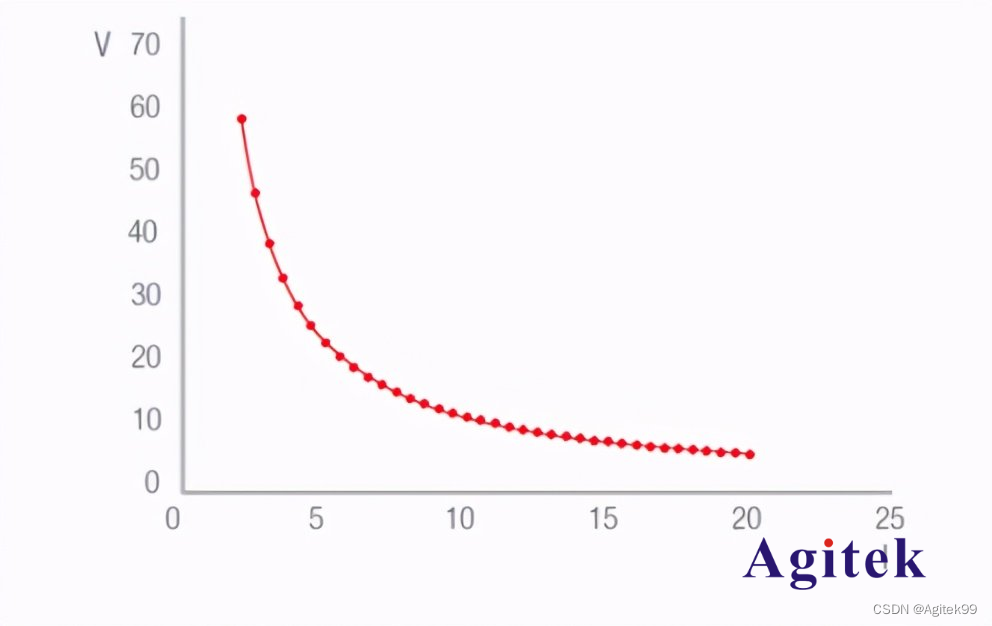
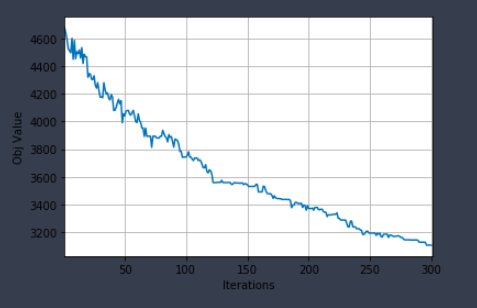
a.绘制目标函数收敛曲线

# 10.绘制目标函数收敛曲线
def plotObj(obj_list):
    plt.rcParams['font.sans-serif'] = ['SimHei'] #show chinese
    plt.rcParams['axes.unicode_minus'] = False  # Show minus sign
    plt.plot(np.arange(1,len(obj_list)+1),obj_list)
    plt.xlabel('Iterations')
    plt.ylabel('Obj Value')
    plt.grid()
    plt.xlim(1,len(obj_list)+1)
    plt.show()

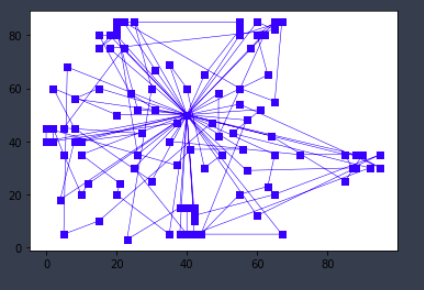
b.绘制优化车辆路径

# 11.绘制优化车辆路径
def plotRoutes(best_sol,depot,node_list):
    """
    best_sol:最优解
    depot:仓库节点 
    node_list:节点的属性卡包集
    """
    for route in best_sol.routes:
        x_coord = [depot.x_coord]
        y_coord = [depot.y_coord]
        for node_no in route:
            x_coord.append(node_list[node_no].x_coord)
            y_coord.append(node_list[node_no].y_coord)
        x_coord.append(depot.x_coord)
        y_coord.append(depot.y_coord)
        plt.plot(x_coord, y_coord, marker='s', color='b', linewidth=0.5)
    plt.show()

c.输出优化结果至xlsx

# 12.输出优化结果
def outPut(best_sol,):
    work=xlsxwriter.Workbook('result.xlsx')#创建一个名为‘result'的workbook
    worksheet=work.add_worksheet()
    worksheet.write(0,0,'opt_type')
    worksheet.write(1,0,'obj')
    worksheet.write(0, 1, 'drive distance of vehicles')#优化目标:距离最小
    worksheet.write(1,1,best_sol.obj) #最优解的目标值
    for row,route in enumerate(best_sol.routes):
        route.insert(0,depot.id)#在route起始位置插入depot的ID
        route.append(depot.id)#在route终点位置插入depot的ID
        worksheet.write(row+2,0,'v'+str(row+1))#写入v1,v2,..
        r=[str(i)for i in route]
        worksheet.write(row+2,1, '-'.join(r))#写route的节点
    work.close()

I. 主函数的运行

将前面定义的所有函数声明后,运行主程序即可.


# 主函数运行
## 1.设置相关变量
vehicle_cap=80
popsize=100
n_select=80
epochs=300#循环迭代次数
## 2.读取文件
depot, node_list,node_seq_no_list=readXlsxFile("cvrp.xlsx")#depot是仓库节点
# node_list时节点的属性卡集,node_seq_no_list时节点映射的ID号
number_of_nodes=len(node_list)#需求节点的个数 
## 3. 生成初始种群
sol_list=genInitialSol(popsize)  
## 4. 实例化最优解best_sol属性
best_sol=Sol()
best_sol.obj=float('inf')
history_best_obj = []#用于存放历史最优解
## 5. 循环迭代
for ep in range(epochs):
    # a.计算当前种群的适应度
    best_sol,sol_list=calFit(sol_list)
    # b.二元锦标赛(选择纯种物种)
    sol_list=selectSol(sol_list)
    # c.当前种群交叉
    sol_list=crossSol(sol_list,number_of_nodes)
    # d.当前种群变异
    sol_list=muSol(sol_list,number_of_nodes)
    # e.最优解的目标值,历史保存
    history_best_obj.append(best_sol.obj) 
    # f.输出当前最优解的目标值
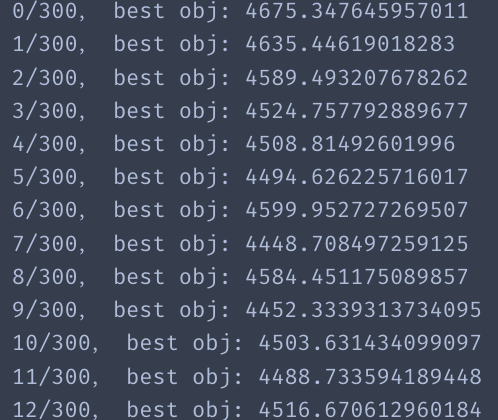
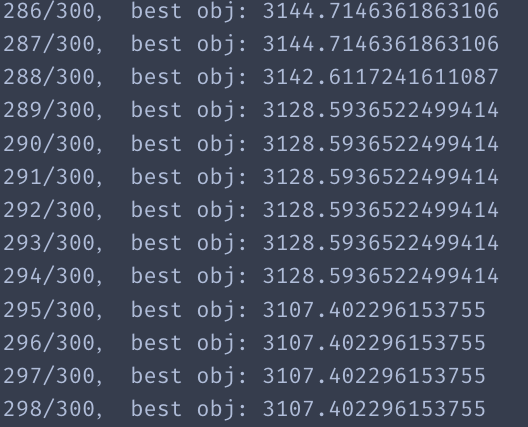
    print("%s/%s， best obj: %s" % (ep,epochs,best_sol.obj))

plotObj(history_best_obj)
plotRoutes(best_sol,depot,node_list)
outPut(best_sol)

结果展示
在这里插入图片描述

附录一:随机种子的作用

li=[1,2,3,4,5,6,7,8]
seed=random.randint(0,10)
random.seed(seed)#随机种子
random.shuffle(li)#打乱序列
print("随机数种子为",seed,"打乱后的序列为:",li)

结果一:
随机数种子为 1 打乱后的序列为: [4, 7, 2, 6, 8, 1, 5, 3]
结果二:
随机数种子为 7 打乱后的序列为: [7, 8, 3, 5, 1, 4, 2, 6]
结果三:
随机数种子为 5 打乱后的序列为: [7, 4, 2, 1, 8, 3, 6, 5]

文章思考:

如何获得CVRP的解. 这里通过分割VRP的解. 那么其他的问题HRPTW的解又是如何获得的呢?
一个序列如何交叉和突变的方法. 理论上应该适用于所有的基因遗传算法.