题目省略了

题解

很多题解都写的是，求正方形矩阵在原矩阵的等效位置的数量，但是不画图可能不好理解，比如我现在有个 3*3 的矩阵，需要用2*2的正方形填充

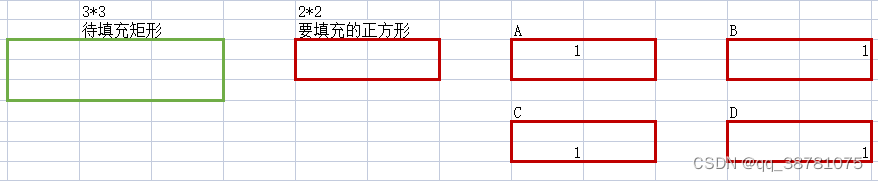
上图中我枚举了所有的点在小正方形可能出现的情况（A、B、C、D），如上图

然后我再枚举所有情况（A、B、C、D），在大矩形的等效位置的数量，如下图

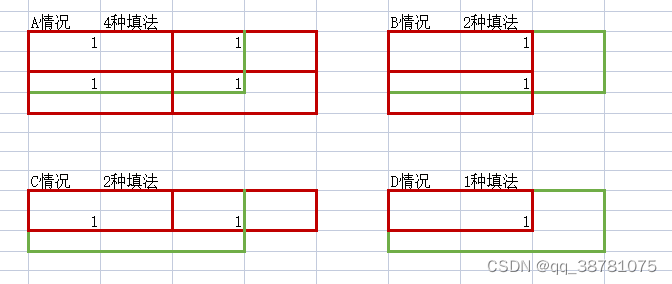
这等效位置的数量，存储在下面代码块的对象 v 里，计算过程在下面 for 循环里，我们在不讨论 maxOnes 是多少的情况下，我们先计算出这个 v

现在我们来讨论 maxOnes：

当 maxOnes 为 1 时，我们选择最大的 A 情况，结果为 4

当 maxOnes 为 2 时，我们选择最大的 A 情况，加上次大的 B 情况或者 C 情况，结果为 4+2

当 maxOnes 为 3 时，我们选择最大的 A 情况，以及 B、C情况，结果为 4+2+2

当 maxOnes 为 4 时，我们选择所有情况，结果为 4+2+2+1

选择最大次大，也是我们代码里要排序的原因

我们拿到了这样一个数组 v，v 里面的值是每一个正方形点位可能出现在矩阵中的等效位置的数量，最后求和过程其实就是往矩阵里面放点，点和点之间不会互相影响，所以可以直接求和

ps：题目中没有要求每个小正方形都要放够 maxOnes 个点，只是最多放 maxOnes 个点

代码

class Solution {
public:
    int maximumNumberOfOnes(int width, int height, int sideLength, int maxOnes) {

        // 用于存储正方形矩阵的每个点在原矩阵的等效位置的数量
        vector<int> v;

        // 求正方形矩阵的每个点在原矩阵的等效位置的数量
        for(int i=0;i<sideLength;++i)
            for(int j=0;j<sideLength;++j) {
                int x=(width-i-1)/sideLength +1;
                int y=(height-j-1)/sideLength +1;
                v.push_back(x*y);
            }
        
        int sum=0;

        // 排序数量多的放前面
        sort(v.begin(), v.end(), greater<int>());

        // 取得前 maxOnes 个点的和
        for(int i=0;i<maxOnes;i++)
            sum+=v[i];
        
        return sum;
    }
};