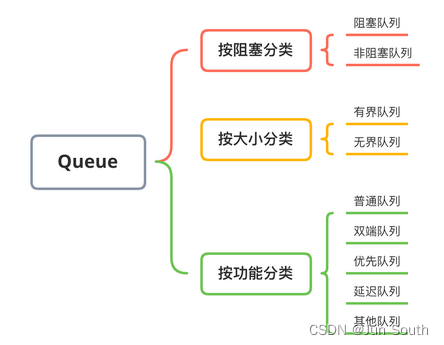
Morris遍历-
- 验证二叉搜索树
- 题目描述
- Morris 遍历解题
- 代码演示:
- morris 遍历改写后序遍历
验证二叉搜索树
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/validate-binary-search-tree
题目描述
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例1:
输入:root = [2,1,3]
输出:true
示例2:
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
Morris 遍历解题
不了解morrisb遍历的可以看遍历二叉树的神级方法–Morris遍历
采用morris 遍历的好处就是,时间复杂度是O(n) 空间复杂度是O(1).和递归遍历树的好处就是,节省了空间,但是造成代码更复杂,流程也更复杂了,因此这当做一个扩展知识,
首先我们知道搜索二叉树,满足在中序遍历时是递增的,因为中序遍历顺序是左头右的顺序,刚好满足搜索树的递增条件,
因此解决用morris 遍历解决这个题,只需要在morris 遍历时,构造出中序遍历,就可以判断了,
morris 遍历改写前序和中序遍历可以查看
二叉树Morris遍历改写成前序遍历和中序遍历
代码演示:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isValidBST(TreeNode root) {
if (root == null){
return true;
}
TreeNode cur = root;
TreeNode mostRight = null;
Integer pre = null;
boolean ans = true;
while (cur != null){
mostRight = cur.left;
if (mostRight != null){
while (mostRight.right != null && mostRight.right != cur){
mostRight = mostRight.right;
}
if (mostRight.right == null){
mostRight.right = cur;
cur = cur.left;
continue;
}else{
mostRight.right = null;
}
}
if (pre != null && pre >= cur.val){
ans = false;
}
pre = cur.val;
cur = cur.right;
}
return ans;
}
}
morris 遍历改写后序遍历
二叉树Morris遍历改写成后序遍历