1. JS散度的问题

上一篇博客从VAE到Diffusion生成模型详解(2)：生成对抗网络GAN中提到普通GAN判别器部分实际上就是求$P_G$和$P_{data}$两个分布的JS散度。但是JS散度最大的缺陷就是，当两个分布不重合时，JS散度就是一个常量$log2$，具体推理可查看理解JS散度(Jensen–Shannon divergence)，这在学习算法中是比较致命的，这就意味这这一点的梯度为 0，梯度消失了。

2. LSGAN(Least Square GAN)

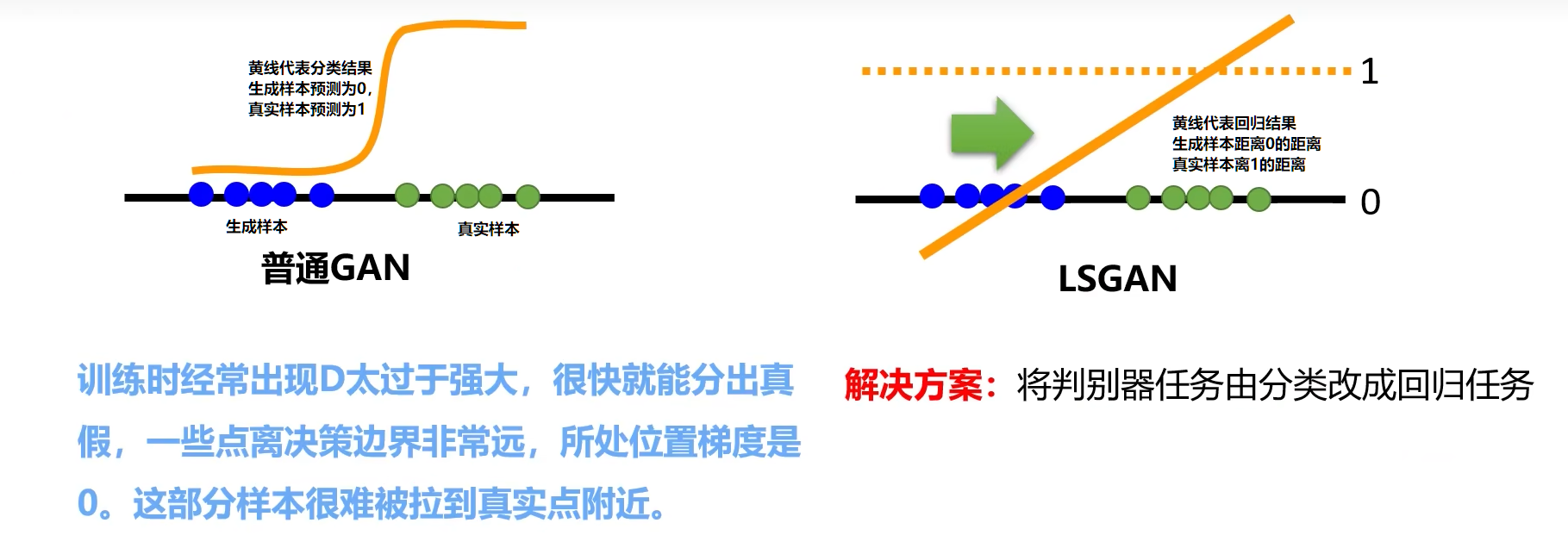
LSGAN使用回归的方法代替了原先判别器分类的方法，原先分类的时候JS散度输出是一个常量，造成优化器不知道往什么方向优化，LSGAN使用回归的方式计算生成样本与0的距离，真实样本与1的距离，随着迭代优化的进行，使得距离越来越小。具体改进点如下：

• 网络结构上：最后一层换为linear层，去掉sigmoid
• 损失函数上：用L1或L2距离代替原先的交叉熵
  

LSGAN目标函数

普通GAN的目标函数如下：

$$\underset{{\theta }_g}{\min }\underset{{\theta }_d}{\max }\left[E_{x\sim p_{data}}\log D_{{\theta }_d}(x)+E_{z\sim p(z)}\log (1-D_{{\theta }_d}(G_{{\theta }_g}(z)))\right]$$

LSGAN的目标函数如下

$$\begin{array}{rl}\underset{D}{\min }{V}_{\mathrm{LSGAN}}(D)& =\frac{1}{2}{\mathbb{E}}_{\mathbf{x}\sim p_{\text{data }}(\mathbf{x})}\left[(D(\mathbf{x})-b{)}^2\right]+\frac{1}{2}{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}\left[(D(G(\mathbf{z}))-a{)}^2\right]\\ \underset{G}{\min }{V}_{\mathrm{LSGAN}}(G)& =\frac{1}{2}{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}\left[(D(G(\mathbf{z}))-c{)}^2\right]\end{array}$$

一般来说$a=-1,b=1,c=1$

下面展示了LSGAN的数学推导，可见优化普通GAN最后等价优化JS散度，而优化LSGAN最后实际等价优化的是卡方距离，卡方距离相关知识可参考机器学习中的数学——距离定义（十八）：卡方距离（Chi-square Measure）

3. WGAN（wasserstein GAN）

WGAN和LSGAN一样，也是针对JS散度在两个分布差别较大时输出为常量的问题，如下图所示，只要$P_G$和$P_{data}$补充叠，无论两者距离多远，JS散度输出都是常量log2

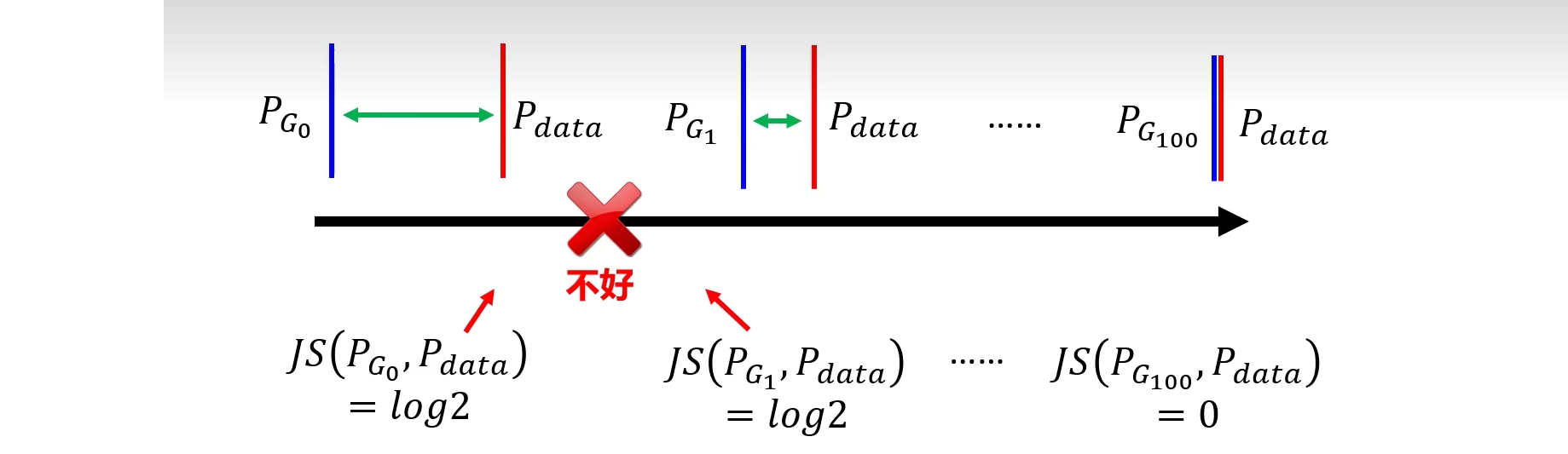
WGAN使用“推土机距离”代替了普通GAN中的JS散度，所谓推土机距离如下图所示，会先进行分块，然后将相应的快推导合适的地方，详情可参考EMD(earth mover’s distances)距离

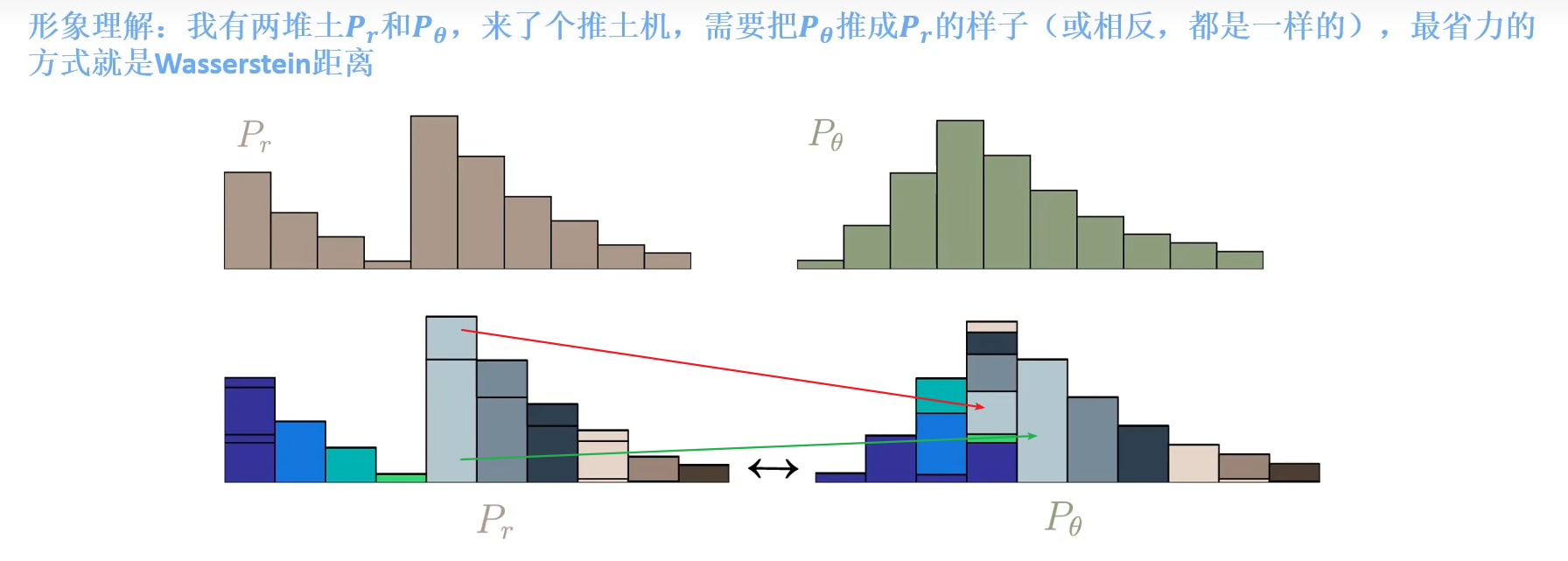
对一个方案$\gamma$，则在$\gamma$方案下的距离为

$$B(\gamma )=\sum _{x_p,x_q}\gamma (x_p,x_q)||x_p-x_q||$$
其中$\gamma (x_p,x_q)$代表需要转运的土的量，即上图中的块，$||x_p-x_q||$表示转移的距离。那么最终结果的距离为：

$$W(P,Q)=\underset{\gamma \in \Pi }{\min }B(\gamma )$$

即选择距离最小的方案作为最终距离

WGAN的目标函数

普通GAN的判别器目标函数如下
$$V(G,D)=E_{x\sim P_{data}}[logD(x)]+E_{x\sim P_G}[log(1-D(x)]$$

而经过一系列的推导后WGAN描述P_{data}和P_G的距离为：

V ( G , D ) = max ⁡ D ∈ 1 − L i p s c h i t z { E x ∼ P d a t a [ D ( x ) ] − E x ∼ P G [ D ( x ) ] } V(G,D)=\operatorname*{max}_{D\in\mathbf{1-Lipschi t z}}\{E_{x\sim P_{d a t a}}[D(x)]-E_{x\sim P_{G}}[D(x)]\} V(G,D)=D∈1−Lipschitzmax​{Ex∼Pdata​​[D(x)]−Ex∼PG​​[D(x)]}

Lipchitz函数

$$||f(x_1)-f(x_2)||\le K||x_1-x_2||$$

即

$$\frac{||f(x_1)-f(x_2)||}{||x_1-x_2||}\le K$$

K=1， 就是1-Lipchitz。注意上式中左半部分是求导公式，在1-Lipchitz可约束下就是要控制判别器的输出值不要变化的太快，即梯度不要大于1，防止在优化目标函数时出现真实数据预测为正无穷，生成样本被预测成负为负无穷这种情况而造成无法优化。

4. 条件GAN

普通GAN是给定一个噪声生成一张图片，现在我们需要对网络能够控制，比如给定一个类别让模型生成对应类别的图片。如给定一个猫的类别，加上噪声，让模型生成猫的图片

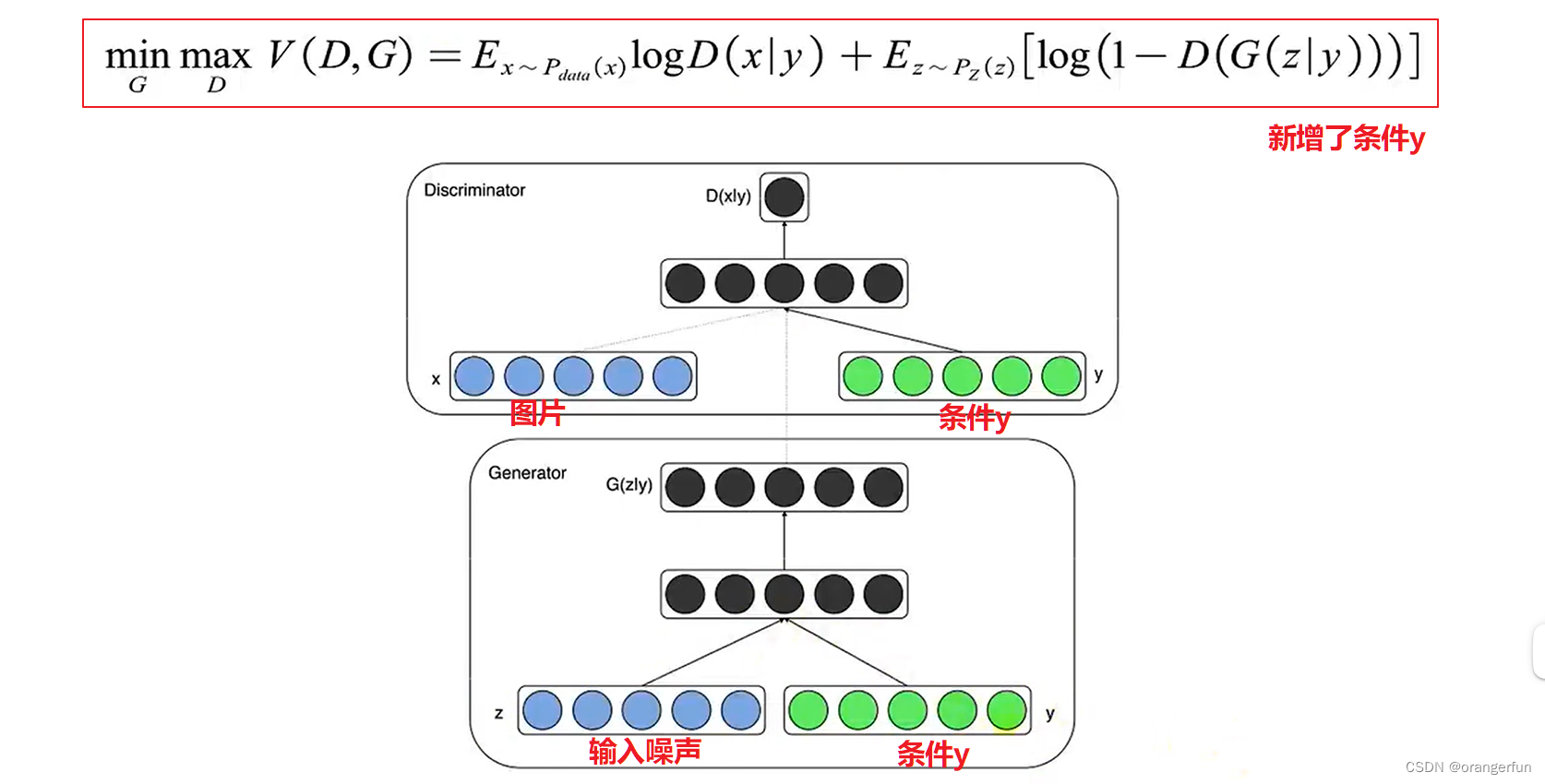
传统GAN的目标函数

$$\underset{G}{\min }\underset{D}{\max }V(D,G)={\mathbb{E}}_{x\sim p_{\mathrm{data}}(x)}[\log D(x)]+{\mathbb{E}}_{z\sim p_z(z)}[\log (1-D(G(z)))]$$

条件GAN的目标函数

$$\underset{G}{\min }\underset{D}{\max }V(D,G)={\mathbb{E}}_{x\sim p_{data}(x)}[\log D(x|y)]+{\mathbb{E}}_{x\sim p_z(z)}[\log (1-D(G(z|y)))]$$

条件GAN的实现有如下几种方式

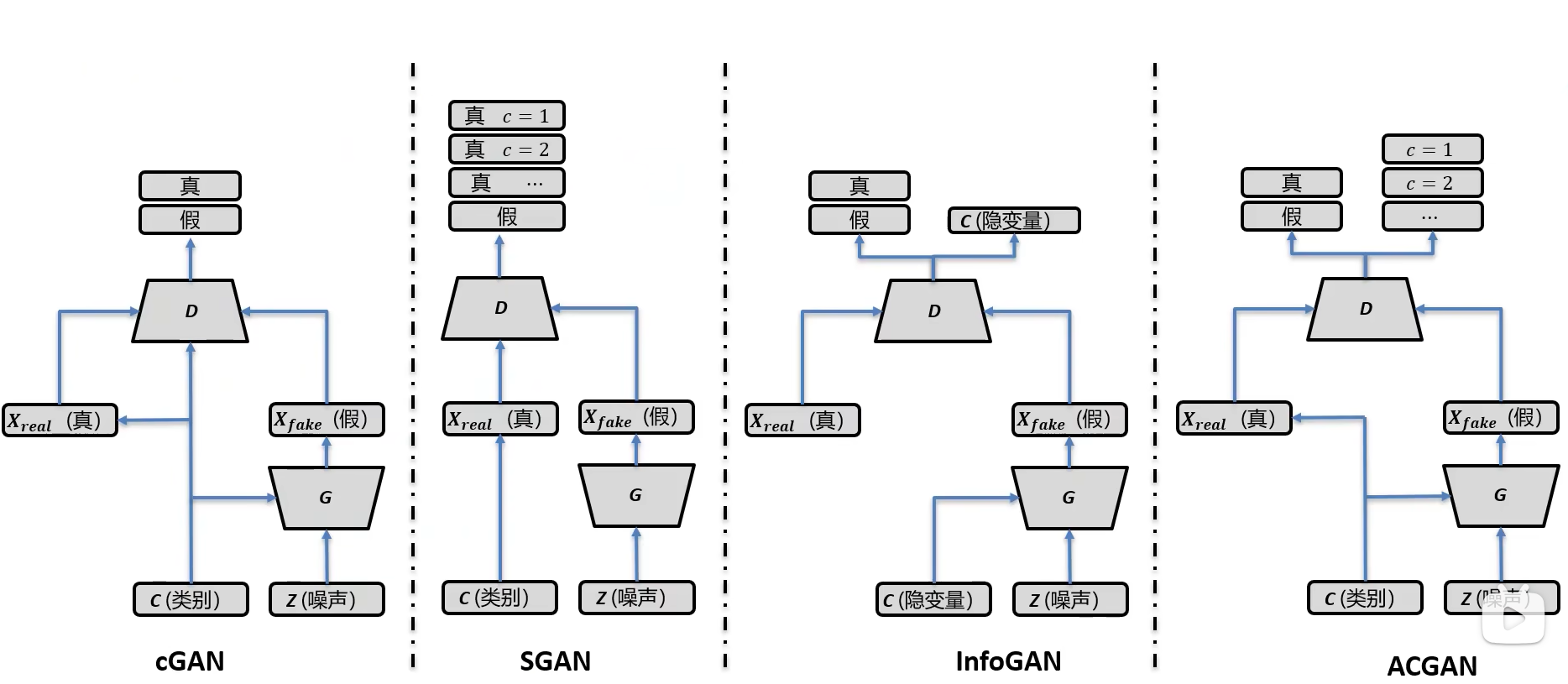
cGAN

cGAN中生成器的输入有两部分：噪声$z$和条件
判别器输入有三个：真实图片$x$，生成图片$\hat{x}$， 条件$c$

SGAN

如下图所示，SGAN的主要区别在于判别器部分，判别器不仅要判断是否为真伪，还要对具体的类别进行分类

ACGAN

ACGAN 的结构如下图所示

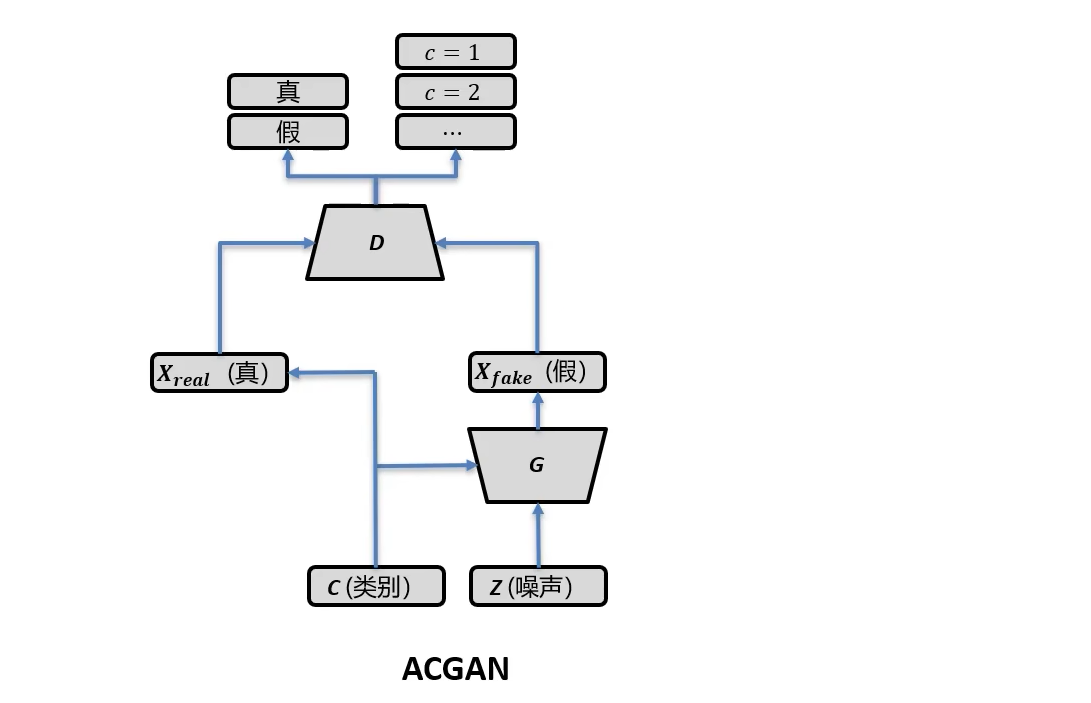
其目标函数如下

$$\begin{array}{rl}& \begin{array}{rl}{L}_S=E[\log P(S=& \text{ real }\mid X_{\text{real }})]+E\left[\log P\left(S=\text{ fake }\mid X_{\text{fake }}\right)\right]\end{array}\\ & L_C=E\left[\log P\left(C=c\mid X_{\text{real }}\right)\right]+E\left[\log P\left(C=c\mid X_{\text{fake }}\right)\right]\end{array}$$

$L_S$是用于区分真假样本，$L_C$用于针对具体类别进行分类

判别器训练时， 最大化 $L_C+L_S$，训练判别器是我们希望对真样本能被识别为真样本，针对生成的样本能被识别成假样本，因此是加上$L_S$。
生成器训练时，最大化 $L_C-L_S$。训练生成器，我们希望生成的图像足够逼真，以至于判别器无法区分真假样本，即真样本被识别为假的，生成的样本被识别为真样本，因此是减去$L_S$

InfoGAN

InfoGAN的结构如下图所示，InfoGAN中使用了隐变量$c$，为了方便讲述隐变量的作用，我们假设当前隐变量是一个三维向量$c=[c_1,c_2,c_3]$，如（a）图所示，当我们改变$c_1$的值时，最后会生成不同的数字，如（c）图所示，当我们改变$c_2$的值时，生成图片的角度会发生改变，如（d）图所示，当我们改变$c_3$时，生成图片的字体大小会发生变化。即我们可控制变量，且变量的每一维度都有明确的意义。

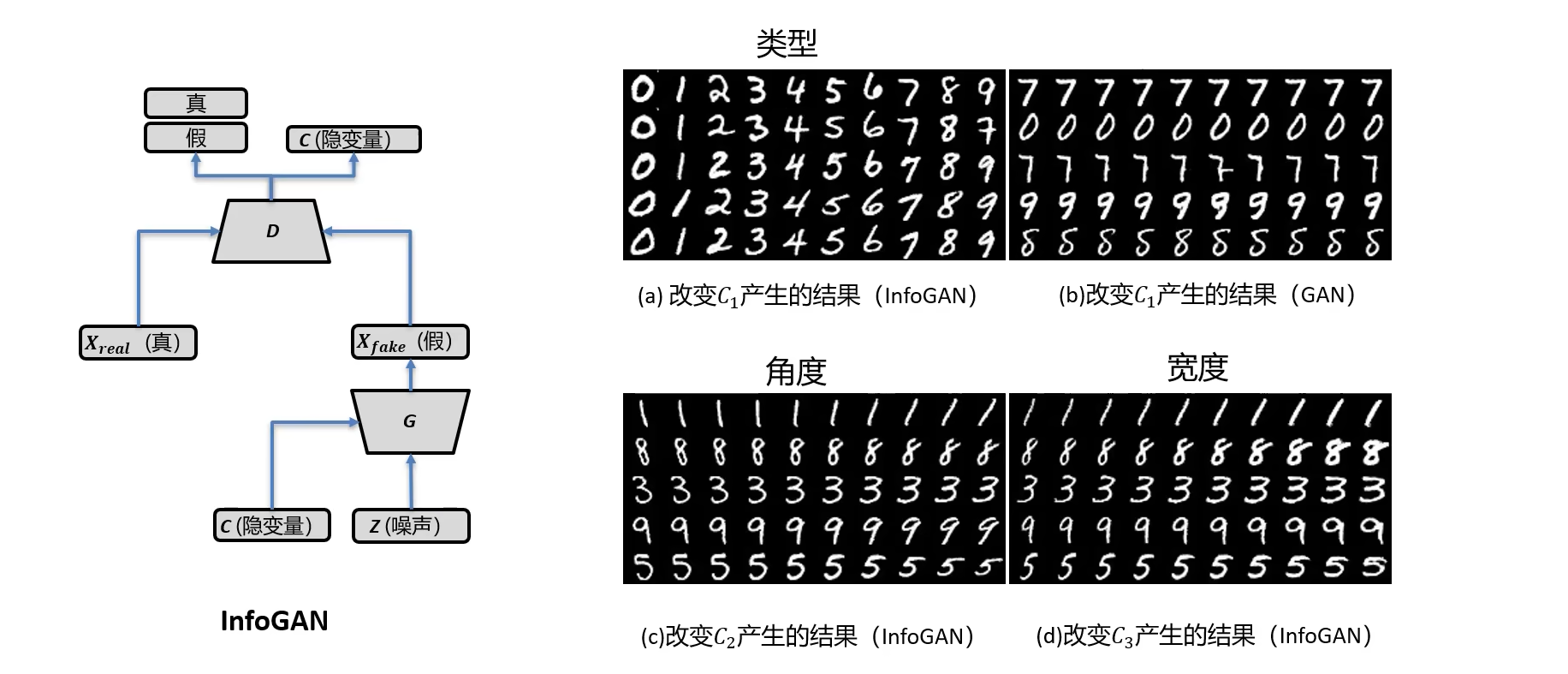
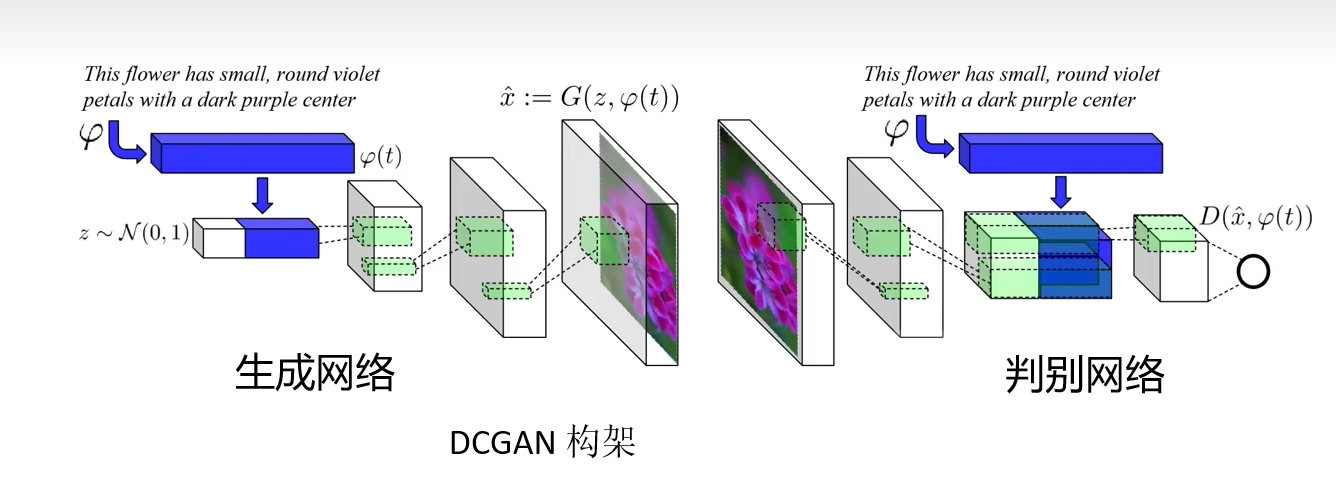
text2image

文本到图像的生成，首先将文本用自然语言模型表征成向量，然后和噪声concat到一起作为新的噪声，输入到网络中进行生成。判别器不仅要判断图片的真假，还要判断图像与文字是否匹配。此外，还需要让模型学会插值，$E_{t_1,t_2\sim p_{data}}[log(1-D(G(z),\beta t_1+(1-\beta )t_2))]$，即$t_1$是一段文本的向量，$t_2$是另一段文本的向量，我们期望$t_1,t_2$的组合包含两者的信息。

stack GAN
stack GAN结构如下图所示，先生成小图，然后将小图特征送入下一层网络再生成大一点的图，如此堆叠下去，和拉普拉斯GAN很像，step by step 的生成。

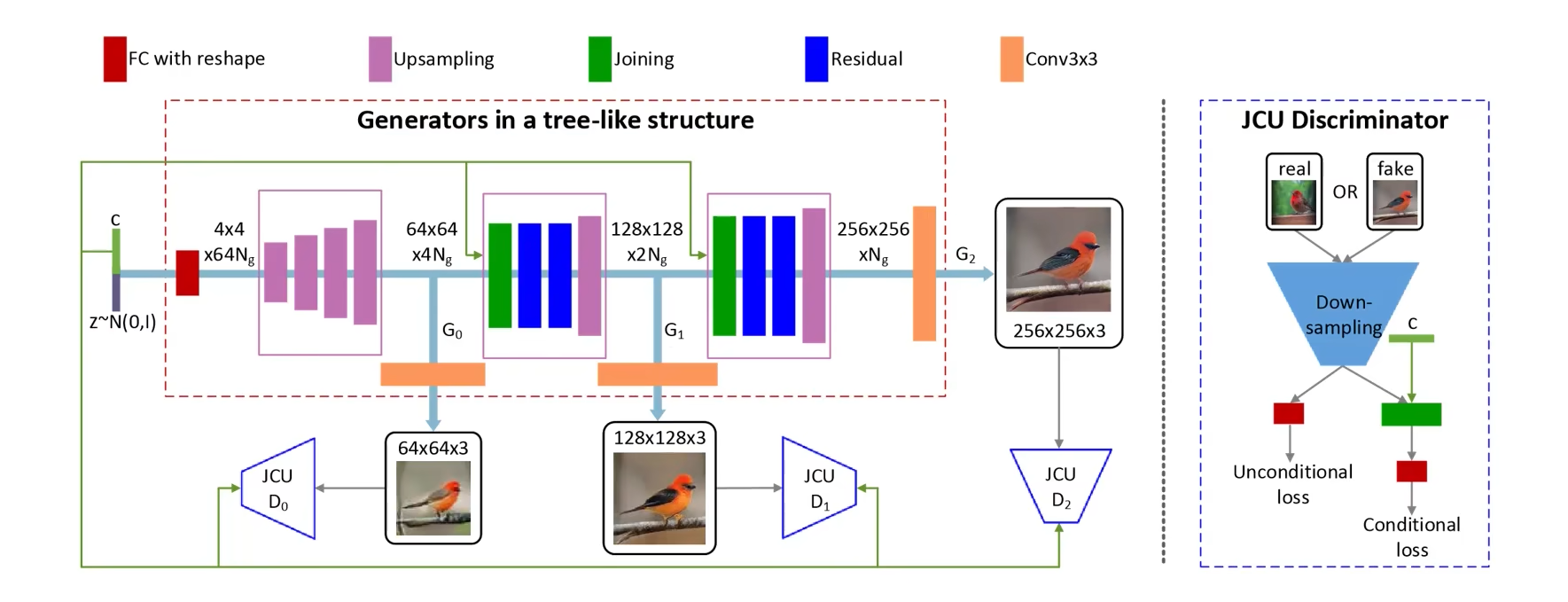
image2image

iGAN
如下图所示，iGAN主要是解决再原始图片上通过画笔修改即可生成对应的图片

iGAN主要操作图像的隐变量，即先将原始图片编码成向量$z$，然后操作该向量。其目标函数如下：
z ∗ = arg ⁡ min ⁡ z ∈ Z { ∑ g ( L g ( G ( z ) , v g ) ⏟ data term  + λ s ⋅ ∥ z − z 0 ∥ 2 2 ⏟  manifold   smoothness  } . z^*=\underset{z \in \mathbb{Z}}{\arg \min }\{\underbrace{\sum_g\left(\mathcal{L}_g\left(G(z), v_g\right)\right.}_{\text {data term }}+\underbrace{\lambda_s \cdot\left\|z-z_0\right\|_2^2}_{\begin{array}{c} \text { manifold } \\ \text { smoothness } \end{array}}\} . z∗=z∈Zargmin​{data term  g∑​(Lg​(G(z),vg​)​​+ manifold  smoothness ​ λs​⋅∥z−z0​∥22​​​}.

损失函数第一项是约束用户引导图像$v_g$和模型生成图片$G(z)$的差异，其中$L_g$可以看作是像素差异函数，让其两者尽可能相似。第二项中$z_0$是最开始给定图片的隐变量，即我们当前的隐要求的隐变量不能和原始图片对应的隐变量相差太大。

Pix2Pix
如下图所示，Pix2Pix主要解决给定草图，生成真实图片的场景

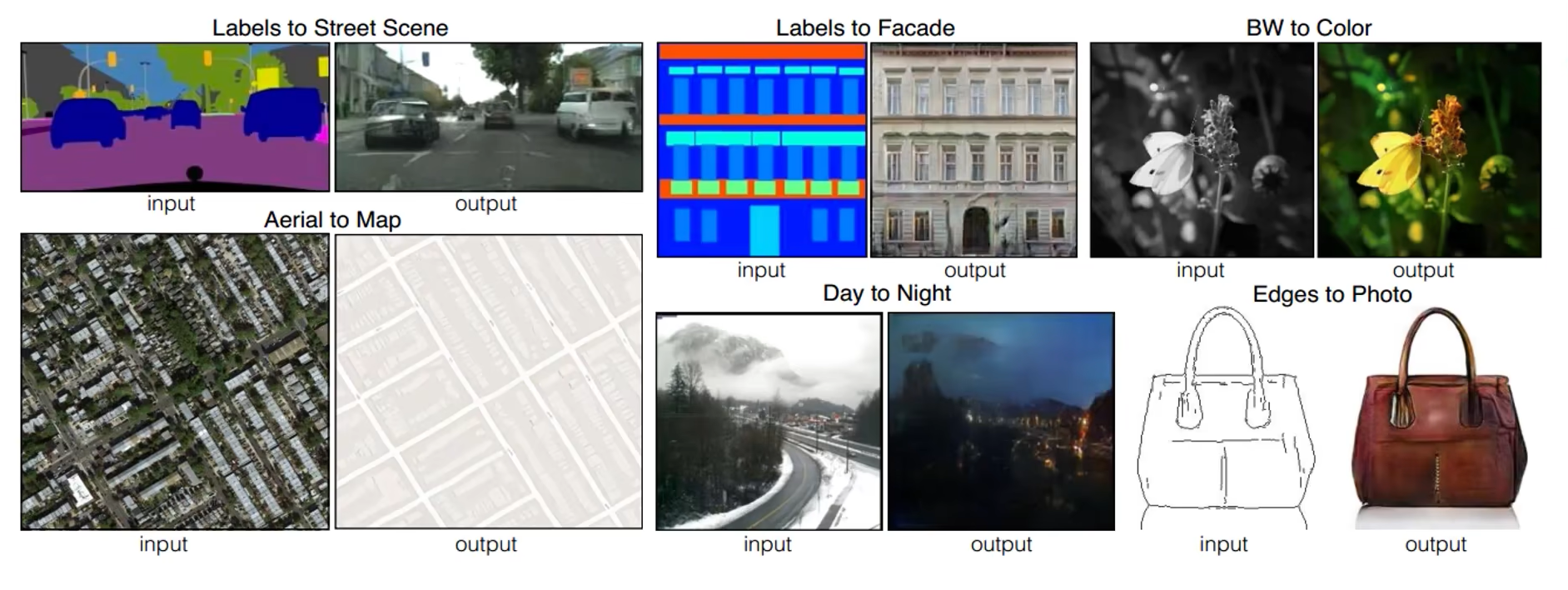
其目标函数如下所示，与普通GAN相比，pix2pix最大不同在于，判别器的输入有两个：草图和生成的图片。下式中$x$是草图，$y$是真实图片， $G(x)$是根据草图生成的图片

$$\underset{G}{\min }\underset{D}{\max }{\mathbb{E}}_{x,y}[\log D(x,y)+\log (1-D(x,G(x))\left)\right]$$

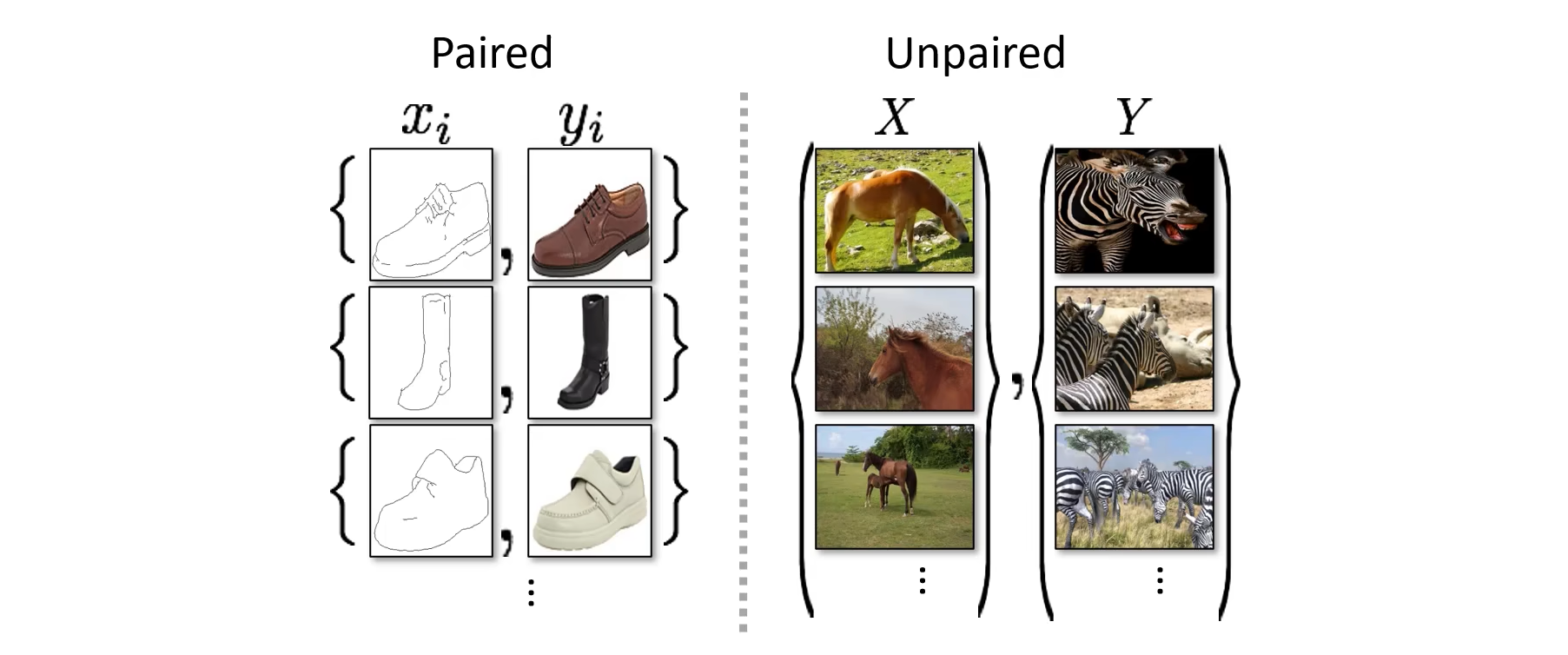
CycleGAN
pix2pix训练需要如下图作伴部分的pair对，而实际中这种pair对比较少，而像右边的这种unpair的情况更多

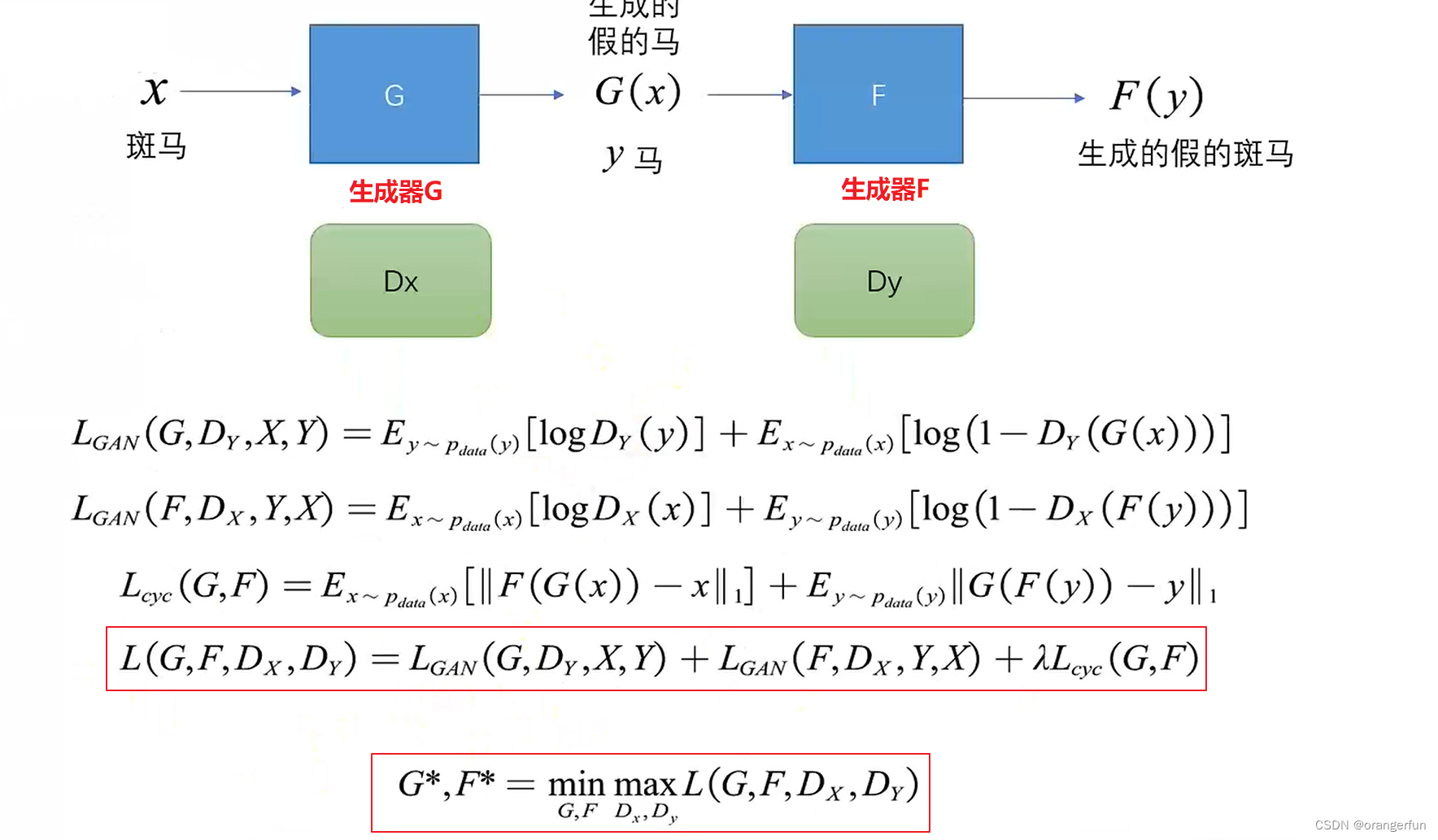
主要流程如下

参考

理解JS散度(Jensen–Shannon divergence
从VAE到Diffusion生成模型详解(2)：生成对抗网络GAN
计算机视觉与深度学习 北京邮电大学 鲁鹏
机器学习中的数学——距离定义（十八）：卡方距离（Chi-square Measure）
EMD(earth mover’s distances)距离

了解更多AI算法，关注微信公众号 funNLPer