目录

1. 二叉树创建字符串。OJ链接

2. 二叉树的分层遍历1。OJ链接

3. 二叉树的分层遍历2。OJ链接

4. 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先 。OJ链接

5. 二叉树搜索树转换成排序双向链表。OJ链接

6. 根据一棵树的前序遍历与中序遍历构造二叉树。 OJ链接

7. 根据一棵树的中序遍历与后序遍历构造二叉树。OJ链接

8. 二叉树的前序遍历，非递归迭代实现 。OJ链接

9. 二叉树的中序遍历 ，非递归迭代实现。OJ链接

10. 二叉树的后序遍历 ，非递归迭代实现。OJ链接

---

1. 二叉树创建字符串。OJ链接

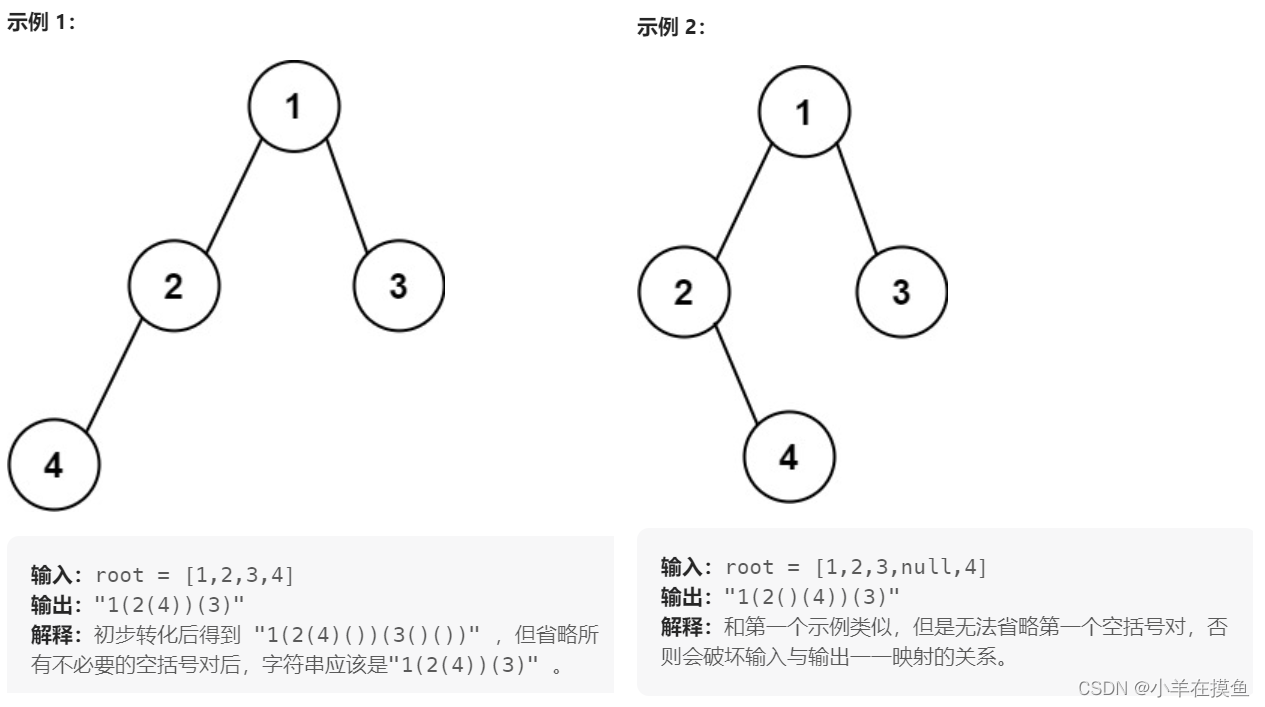
分析题型如下：

根据示例可以看到其省的括号并不是把所有的都省了，而是会保留左子树的括号
左右都为空省略，左为空不能省略，右为空可以省略

思路：

用递归遍历整棵树，注意要将每个节点的值转为字符串类型，再利用重载的+=来添加括号

我们先写一个不省略括号的代码，然后根据之前的三个条件进行限制

不省略括号的代码如下：

根据条件加入限制得到：

class Solution {
public:
    string tree2str(TreeNode* root) {
        if(root == nullptr)
            return "";

        string str = to_string(root->val);

        // 先判断左是否为空，不为空：继续；为空：再判断右为不为空；
        // 不为空：左不能省，继续；
        // 为空，那么此时左右都为空，就可以省略了。
        if(root->left || root->right)
        {
            str += '(';
            str += tree2str(root->left);
            str += ')';
        }

        // 在上面条件判断后，再判断右是否为空
        // 如果右为空：省略；右不为空：继续。
        if(root->right)
        {
            str += '(';
            str += tree2str(root->right);
            str += ')';
        }
        
        return str;
    }
};

2. 二叉树的分层遍历1。OJ链接

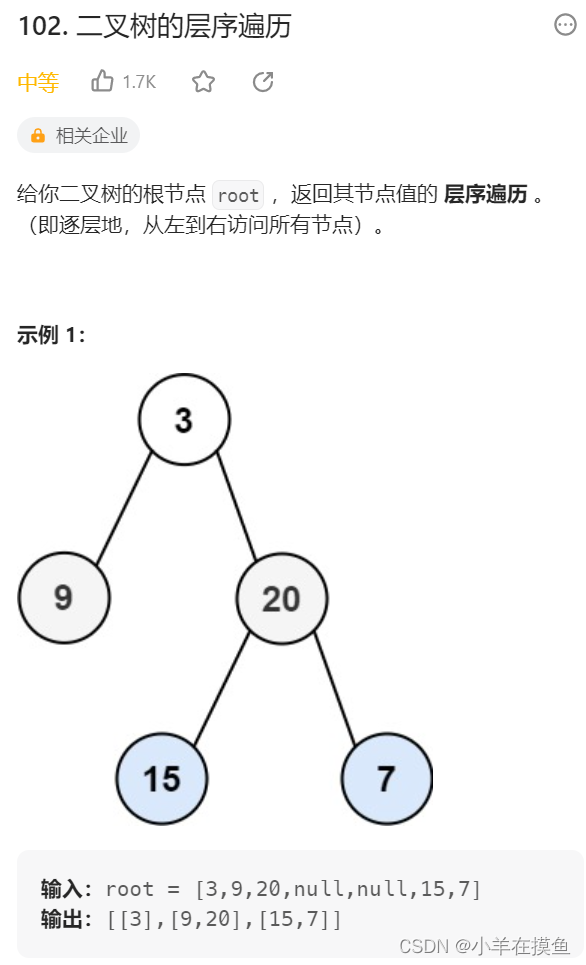
思路：

用一个队列来存放数据，在这个队列出数据的时候，将其的左右节点入栈，
再定义一个变量 levelsize 用来存储该层有多少个数

具体如下图：

代码：

class Solution {
public:
    // vector<vector<int>>二维数组
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> q;
        int levelsize = 0;

        if(root)
        {
            q.push(root);
            levelsize = 1;
        }

        vector<vector<int>> vv;

        //当队列为空时结束
        while(!q.empty())
        {
            // 通过levelsize来控制一层一层的出
            vector<int> v;//把每一层的数据放到一个vector里面

            while(levelsize--)
            {
                TreeNode* F = q.front();//F就是此时要控制的树的节点
                q.pop();
                v.push_back(F->val);

                if(F->left)
                    q.push(F->left);
                if(F->right)
                    q.push(F->right);
            }
            // 将第每一层的数组v放到二维数组中
            vv.push_back(v);
            // 更新下一层的数据
            levelsize = q.size();

        }

        return vv;
    }
};

3. 二叉树的分层遍历2。OJ链接

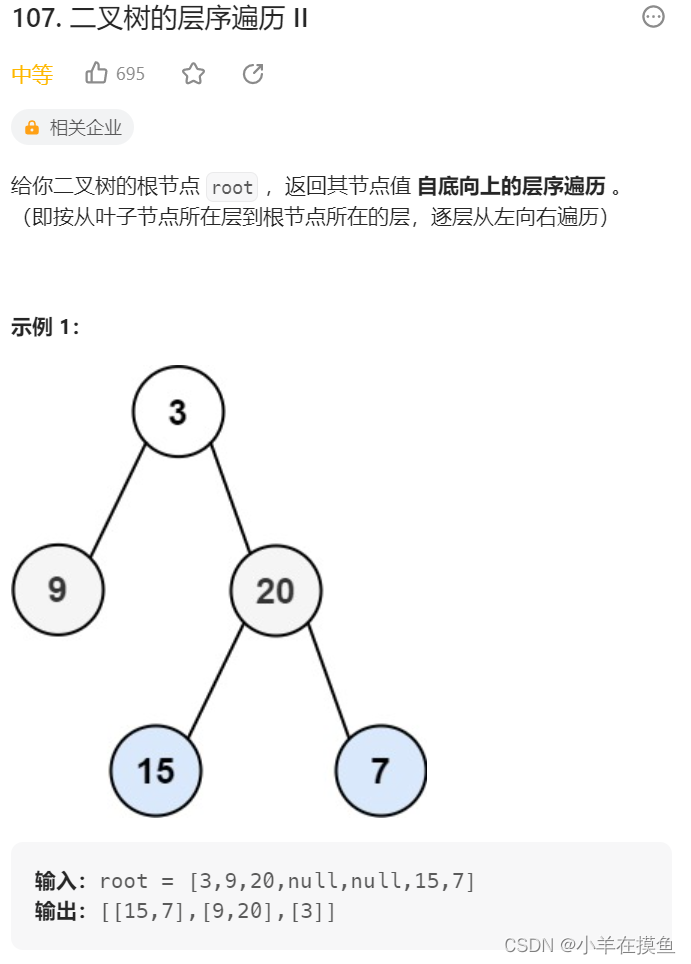
思路：

这道题的思路和上面那道题的思路一模一样，只是我们在最后需要稍微处理一下，使其反转打印

我们C++里面的算法头文件里面有一个reverse的逆置算法

 正好可以用到此问题上

class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
queue<TreeNode*> q;
        int levelsize = 0;

        if(root)
        {
            q.push(root);
            levelsize = 1;
        }

        vector<vector<int>> vv;

        //当队列为空时结束
        while(!q.empty())
        {
            // 通过levelsize来控制一层一层的出
            vector<int> v;//把每一层的数据放到一个vector里面

            while(levelsize--)
            {
                TreeNode* F = q.front();//F就是此时要控制的树的节点
                q.pop();
                v.push_back(F->val);

                if(F->left)
                    q.push(F->left);
                if(F->right)
                    q.push(F->right);
            }
            // 将第每一层的数组v放到二维数组中
            vv.push_back(v);
            // 更新下一层的数据
            levelsize = q.size();

        }
        // 反转
        reverse(vv.begin(), vv.end());
        return vv;
    }
};

4. 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先 。OJ链接

 

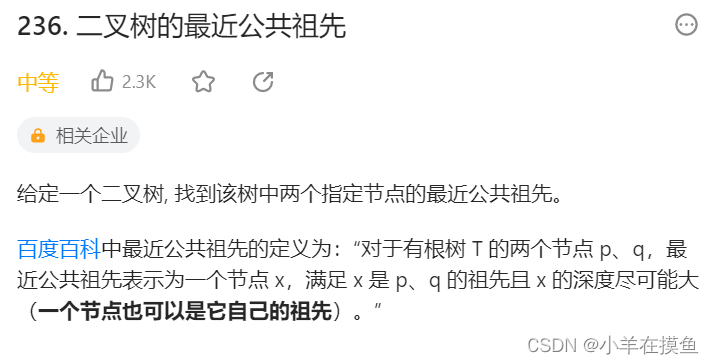
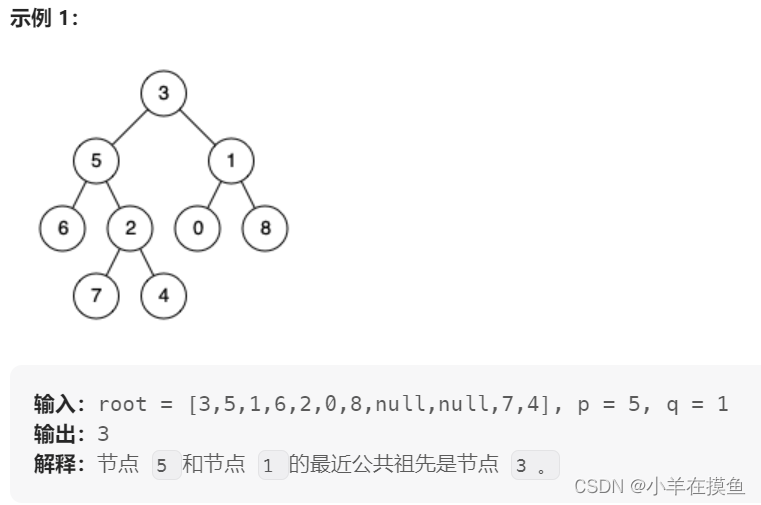
思路1：

首先我们要找最近的公共祖先，那么孩子肯定是在这个公共祖先的一左一右

p、q 是题目给我们的两个数，我们先找这两个数是在，此时节点的左边还是右边

此时会有三种情况：

1）如果p再左，q再右；或者，q在左，p在右。那么此时节点就是最近公共祖先
2）如果都在左，转换为子问题，递归到左子树去找公共祖先
3）如果都在右，转换为子问题，递归到右子树去找公共祖先

class Solution {
public:
    //写判断p、q在左还是右的函数
    bool IsInTree(TreeNode* root, TreeNode* x)
    {
        if(root == nullptr)
        {
            return false;
        }
        if(root == x)
            return true;
        else
            return IsInTree(root->left, x) || IsInTree(root->right, x);
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //跟为空返回空
        if(root == nullptr)
            return nullptr;
        
        //如果p或q有一个为跟，另一个是孩子，root就是最近祖先
        if(p == root || q == root)
            return root;
        
        //判断p、q在左边还是右边
        bool pInLift = IsInTree(root->left, p);
        bool pInRight = !pInLift;

        bool qInLift = IsInTree(root->left, q); 
        bool qInRight = !qInLift;

        //1.如果一个在左，一个在右。那么此时节点就是最近公共祖先
        //2.如果都在左，转换为子问题，递归到左子树去找公共祖先
        //3.如果都在右，转换为子问题，递归到右子树去找公共祖先
        if((pInLift && qInRight) || (qInLift && pInRight))
        {
            return root;
        }
        else if(pInLift && qInLift)
        {
            return lowestCommonAncestor(root->left, p, q);
        }
        else
        {
            return lowestCommonAncestor(root->right, p, q);
        }
    }
};

思路2：

我们可以看到按照思路1来写的代码可以通过，但比较费时间

我们可以来算一下思路1代码的时间复杂度：

可能会有人觉得上述代码的时间复杂度是 O(n*logN)，查找是N，高度是logN

但实际上并不是，我们要注意：只有完全二叉树和满二叉树我们才能认为它的高度是 logN
因为有可能是课歪脖子树，所以上述代码的时间复杂度是 O(n^2)

思路二就是用两个栈来记录p、q的路径，然后将两个路径进行比较

从3的左边开始遍历到6的时候左右都没有，就把6出了

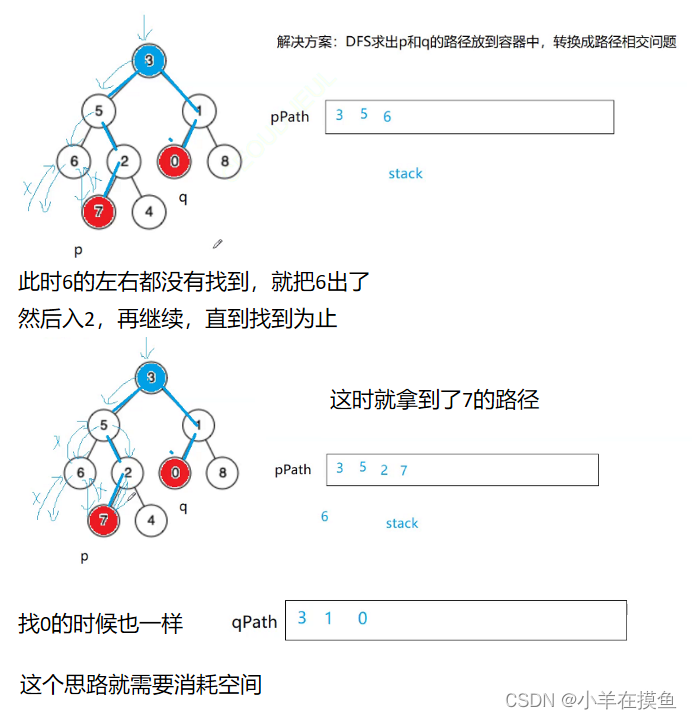
class Solution {
public:
    bool Getpath(TreeNode* root, TreeNode*x, stack<TreeNode*>& path)
    {
        //先写递归结束条件
        if(root == nullptr)
            return false;
        //入栈
        path.push(root);

        // 等于要找的数，结束
        if(root == x)
            return true;

        // 不等于，继续递归找
        if(Getpath(root->left, x, path))
            return true;
        if(Getpath(root->right, x, path))
            return true;

        //递归到头都没找到，则出栈
        path.pop();
        return false;
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) 
    {
        // 定义两个栈，一个存放p的路径，一个存放q的路径
        stack<TreeNode*> pPath, qPath;

        // 找p和q，并记录其路径
        Getpath(root, p, pPath);
        Getpath(root, q, qPath);

        // 将长路径出，直到到和短路径一样长
        while(pPath.size() != qPath.size())
        {
            if(pPath.size() > qPath.size())
                pPath.pop();
            else
                qPath.pop();
        }    

        // 两个一起出，直到他们有相等的值结束
        while(pPath.top() != qPath.top())
        {
            pPath.pop();
            qPath.pop();
        }

        //此时不管是pPath还是qPath的首元素都是最进祖先
        return qPath.top();
    }
};

5. 二叉树搜索树转换成排序双向链表。OJ链接

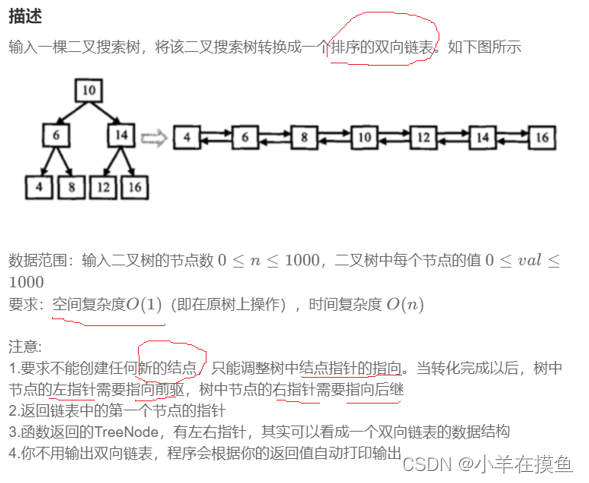
要求里面需要我们在原树上进行修改，并且空间复杂读为 O(1)，
如果没有这个要求，我们就可以将其中序遍历存放到vector中，然后再该链接关系，就会非常简单

思路：

我们还是中序遍历该树，得到：4，6，8，10，12，14，16
同时记录一个前驱prev，一个当前cur；因为是中序遍历，所以一个数的左一定是指向前驱的
此时难点在于找后继节点：我们让cur->left = prev  ，让prev->right = cur
最后，在修改完之后我们只能拿到root跟节点，但这个根节点不是循环链表的头，所以我们只需要去往左走，走到头即可

class Solution 
{
public:
	// prev在递归是不能改变，所以需要引用起别名
	void InorderTraversal(TreeNode* cur, TreeNode*& prev)
	{
		if(cur == nullptr)
			return;
		//中序遍历
		InorderTraversal(cur->left, prev);
		
		cur->left = prev;
		//防止刚开始prev为空
		if(prev)
			prev->right = cur;
		prev = cur;

		InorderTraversal(cur->right, prev);
	}
    TreeNode* Convert(TreeNode* pRootOfTree)
	{
        TreeNode* prev = nullptr;
		InorderTraversal(pRootOfTree, prev);

		TreeNode* head = pRootOfTree;

		// 寻找头结点
		while(head && head->left)
			head = head->left;

		return head;
    }
};

6. 根据一棵树的前序遍历与中序遍历构造二叉树。 OJ链接

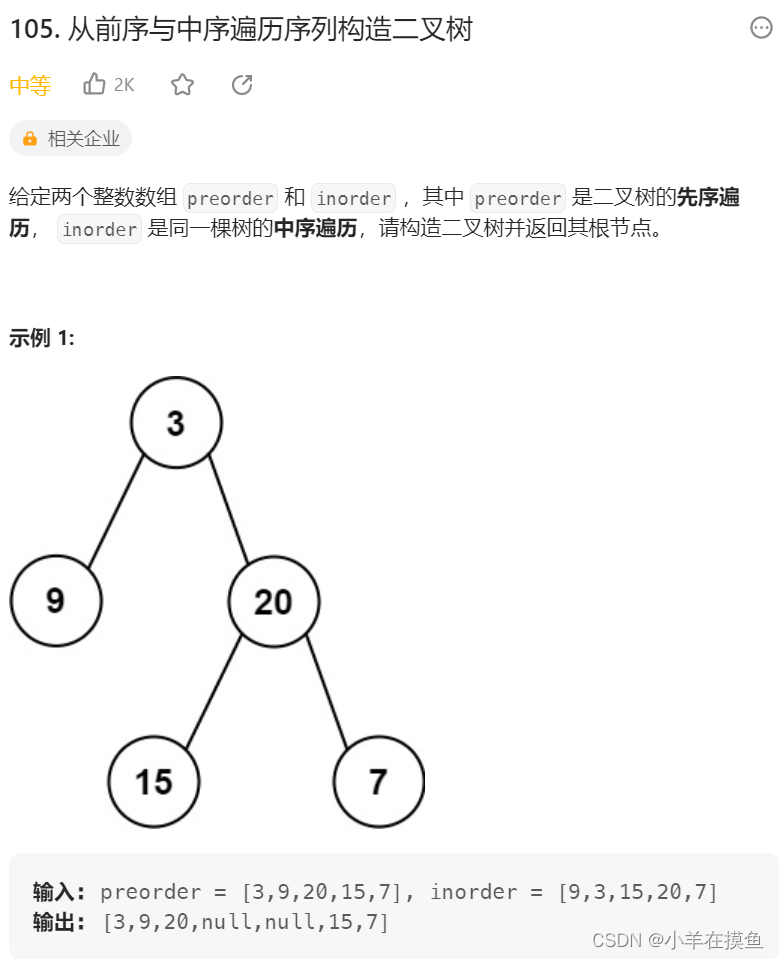
思路：

通过前序数组不断去确定根，然后对中序数组进行空间划分，当空间没有是返回根

class Solution 
{
public:
    // 因为需要递归，不好再原树上进行操作，所以先建立一个子函数
    // int& prei定义前序的一个下标需要一直往后走，中序需要定义一段区间，来分割子树：inbegin、inend
    TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder, int& prei, int inbegin, int inend) 
    {
        // 结束条件
        if(inbegin > inend)
            return nullptr;

        TreeNode* root = new TreeNode(preorder[prei]);

        // 分割出左右区间
        int rooti = inbegin;
        // 再中序数组里面找到根
        while(rooti <= inend)
        {
            //判断中序数组里的值与前序数组里的值是否相等，相等找到，不相等继续找
            if(inorder[rooti] == preorder[prei])
                break;
            else
                rooti++;
        }
        // 此时在前序数组里面找下一个左子树的根节点
        ++prei;

        // 中序数组被分割出了三段区间：[inbegin, rooti-1]; rooti; [rooti+1,inend]
        root->left = _buildTree(preorder, inorder, prei, inbegin, rooti-1);
        root->right = _buildTree(preorder, inorder, prei, rooti+1, inend);
        
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) 
    {
        int i = 0;
        return _buildTree(preorder, inorder, i, 0, inorder.size()-1);
    }
};

7. 根据一棵树的中序遍历与后序遍历构造二叉树。OJ链接

和上一题的解题思路一致，只是把从前序数组的前往后找根节点，换位了，后序数组的从后往前找根节点，需要注意的是，在建立二叉树的过程中，需要先构建右子树，然后再构建左子树

class Solution {
public:
    TreeNode* _buildTree(vector<int>& postorder, vector<int>& inorder, int& prei, int inbegin, int inend) 
    {
        // 结束条件
        if(inend < inbegin)
            return nullptr;

        TreeNode* root = new TreeNode(postorder[prei]);

        // 分割出左右区间
        int rooti = inbegin;
        // 再中序数组里面找到根
        while(rooti <= inend) //rooti <= inend
        {
            //判断中序数组里的值与后序数组里的值是否相等，相等找到，不相等继续找
            if(inorder[rooti] == postorder[prei])
                break;
            else
                rooti++;
        }
        // 此时在后序数组里面找下一个左子树的根节点
        --prei;

        // 中序数组被分割出了三段区间：[inbegin, rooti-1]; rooti; [rooti+1,inend]
        root->right = _buildTree(postorder, inorder, prei, rooti+1, inend);
        root->left = _buildTree(postorder, inorder, prei, inbegin, rooti-1);
        
        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) 
    {
        int i = postorder.size()-1;
        return _buildTree(postorder, inorder, i, 0, inorder.size()-1);
    }
};

8. 二叉树的前序遍历，非递归迭代实现 。OJ链接

思路：

还是用栈，先把左路的数都放入栈，然后再依次出栈，其孩子入栈

• 1.左路节点
• 2.左路节点的右子树

这里的右子树怎么访问？
继续变为子问题，再继续左路节点，如下图详解：

下图中入栈顺序是前序的顺序，出栈顺序是后续的顺序

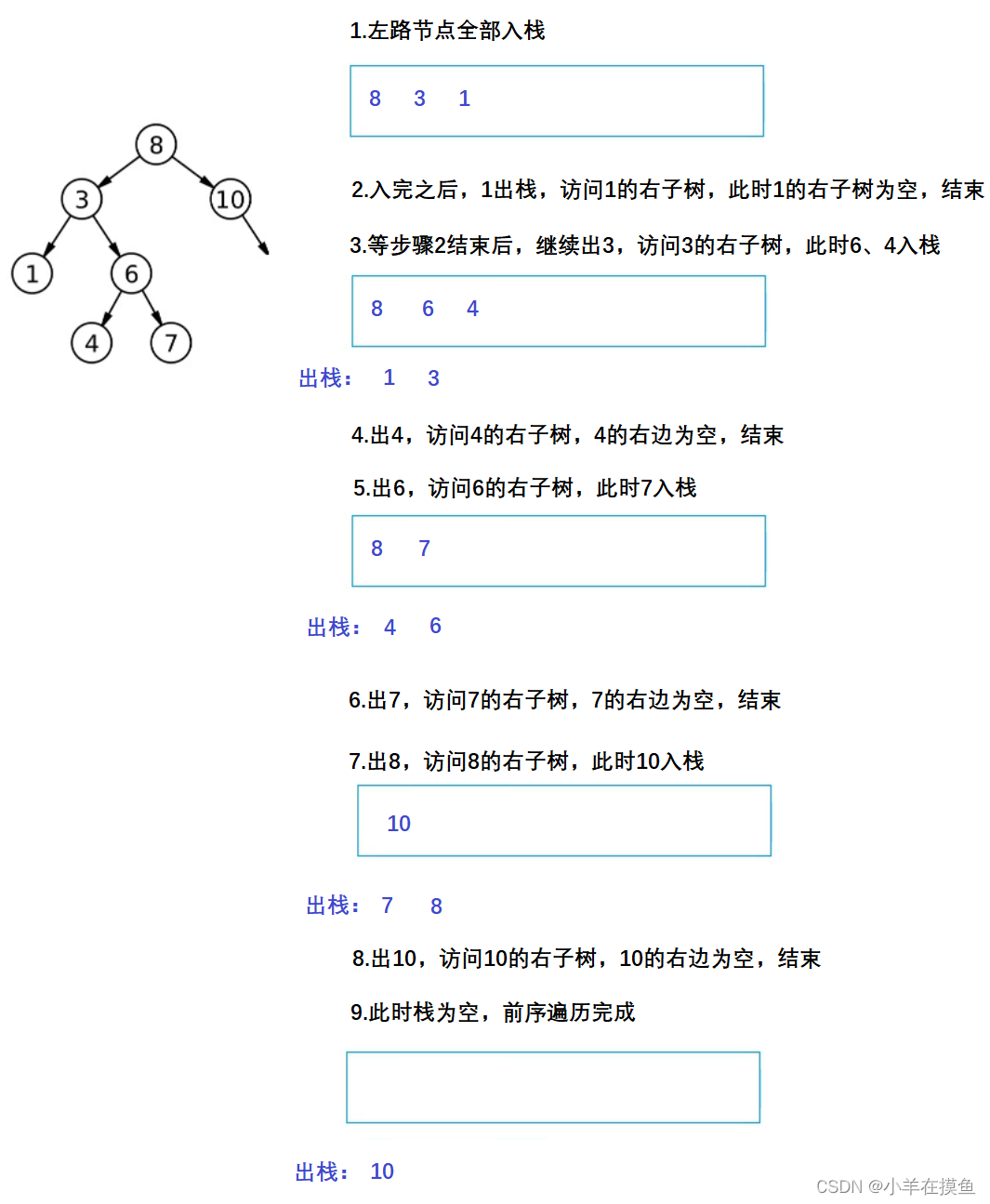
代码如下：

class Solution {
public:
    //  非递归实现：
    vector<int> preorderTraversal(TreeNode* root) 
    {
        // 创建一个栈来存放数据
        stack<TreeNode*> st;
        TreeNode* cur = root;
        // 创建对象v来存放出栈的数据
        vector<int> v;
        // 需要cur为空并且栈为空才会结束
        while(cur || !st.empty())
        {
            // 一直往左边去走，直到左边为空
            while(cur)
            {
                // 入栈前，给数组v尾插数据
                v.push_back(cur->val);
                // 将左树的值入栈
                st.push(cur);
                //继续往左走
                cur = cur->left;
            }

            //左为空后出栈，走右
            //取栈顶数据，然后出栈
            TreeNode* top = st.top();
            st.pop();

            cur = top->right;
        }

        return v;
    }
};

9. 二叉树的中序遍历 ，非递归迭代实现。OJ链接

思路：

和前序队列一样，仔细观察前序队列的图，就可以发现，每次出栈的顺序就是中序队列的顺序，所以下面代码仅仅只是将vector的尾插放在了出栈前而不是入栈前。

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        // 创建一个栈来存放数据
        stack<TreeNode*> st;
        TreeNode* cur = root;
        // 创建对象v来存放出栈的数据
        vector<int> v;
        // 需要cur为空并且栈为空才会结束
        while(cur || !st.empty())
        {
            // 一直往左边去走，直到左边为空
            while(cur)
            {
                // 将左树的值入栈
                st.push(cur);
                //继续往左走
                cur = cur->left;
            }

            //左为空后出栈，走右
            //取栈顶数据，然后出栈
            TreeNode* top = st.top();

            //出栈时，给v里面放入数据，此时将会是中序队列
            v.push_back(top->val);
            st.pop();

            cur = top->right;
        }

        return v;
    }
};

10. 二叉树的后序遍历 ，非递归迭代实现。OJ链接

后序遍历比前序和中序要难思考一点，所以一般笔试什么的都会考后序遍历

思路1：

我们先走左子树，走到最后一个左子树的时候
1）当其右子树为空，我们可以直接拿取
2）当右子树不为空，我们第二次走到父节点时，拿取（举个例子，如下：）
        

        我们会在第二次访问的时候拿取

代码如下：（注意看注释理解）

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        // 创建一个栈来存放数据
        stack<TreeNode*> st;
        TreeNode* cur = root;
        // 创建对象v来存放出栈的数据
        vector<int> v;

        // 加入
        TreeNode* prev = nullptr;

        // 需要cur为空并且栈为空才会结束
        while(cur || !st.empty())
        {
            // 一直往左边去走，直到左边为空
            while(cur)
            {
                // 将左树的值入栈
                st.push(cur);
                //继续往左走
                cur = cur->left;
            }

            //左为空后出栈，走右
            //取栈顶数据，然后出栈
            TreeNode* top = st.top();

            //1、右为空，可以访问跟节点
            //2、右子树已经被访问过了（上一个访问的节点是右子树的根）
            if(top->right == nullptr || top->right == prev)
            {
                v.push_back(top->val);
                st.pop();

                prev = top;
            }
            else
            {
                //访问右子树，子问题
                cur = top->right;
            }
        }
        return v;
    }
};

思路2：

后序遍历的访问方式是：左右根，我们把它逆置一下变为：根右左，
和前序比较可以发现只需要改一下前序代码，
使其先入栈右边的树，然后再入左边的树，最后来个逆置也是可以的！

这种方法也是最简单的，也这算是一个取巧的操作，代码如下：

class Solution {
public:
    //  非递归实现：
    vector<int> preorderTraversal(TreeNode* root) 
    {
        // 创建一个栈来存放数据
        stack<TreeNode*> st;
        TreeNode* cur = root;
        // 创建对象v来存放出栈的数据
        vector<int> v;
        // 需要cur为空并且栈为空才会结束
        while(cur || !st.empty())
        {
            // 一直往右边去走，直到右边为空
            while(cur)
            {
                // 入栈前，给数组v尾插数据
                v.push_back(cur->val);
                // 将左树的值入栈
                st.push(cur);
                //继续往右走
                cur = cur->right;
            }

            //左为空后出栈，走右
            //取栈顶数据，然后出栈
            TreeNode* top = st.top();
            st.pop();

            cur = top->left;
        }
        reverse(v.begin(), v.end());
        
        return v;
    }
};