一、Shadow Mapping回顾

[计算机图形学]光线追踪前瞻：阴影图(前瞻预习/复习回顾)__Yhisken的博客-CSDN博客

关于Shadow Mapping我们在GAMES101中学过，如果不知道可以参考我的博客。

Shadow Mapping是光栅化时为了实现阴影的一种算法，而它实际上是把场景渲染了两次。(Pass1)第一次我们从光源方向出发看向场景，渲染一张深度图，它存储了从光源方向看向场景时各个位置的最浅深度，这里我们设为z。(Pass2)第二次我们从我们真正的摄像机出发看向场景，我们可以得到我们每个像素着色点位置到光源的距离，这里我们假设为d。而用两者相互比较，如果 z<d，那也就说明光源看不见这个着色点，而摄像机能看见，也就说明该点在引用中，这是阴影图的基本思路。(需要注意的是这里的d和z需要在同一种空间下进行比较，因为投影到相机后的z，也就是深度是不等于投影之前的相机到着色点的距离的，也就是说投影之后的深度并不是欧式空间中的距离，对于这个问题我们只需要确保z和d进行比较的时候，要么都是投影之前的值，要么都是投影之后的值就可以了)

Shadow Mapping以下简称SM。SM是一种图像空间的做法，好处就是我们不需要得到场景的几何信息了，而是直接通过生成的Shadow Map去判断光源能不能照到该着色点。

当然SM也有问题，包括阴影的走样，自遮挡现象。

二、Shadow Mapping的问题

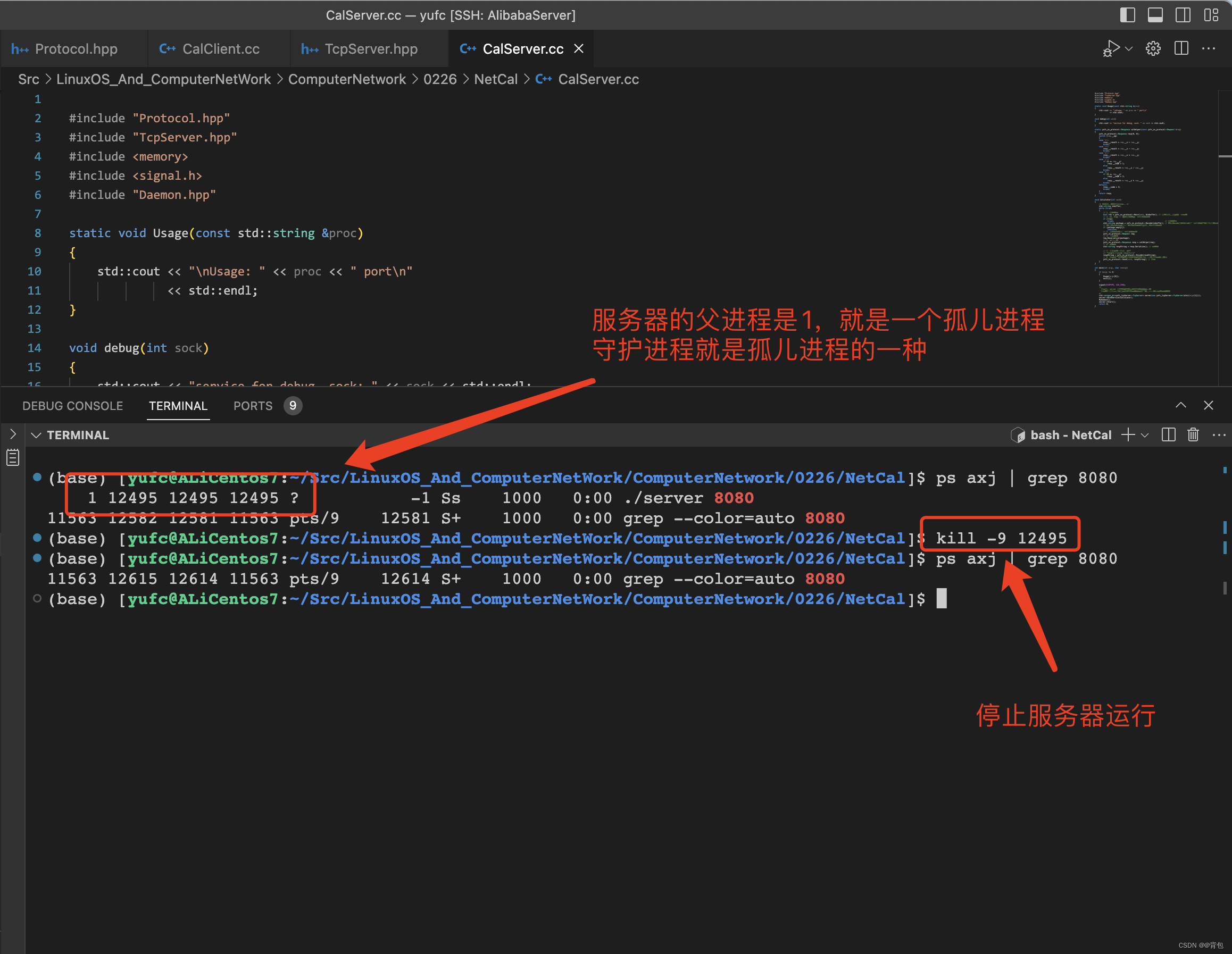
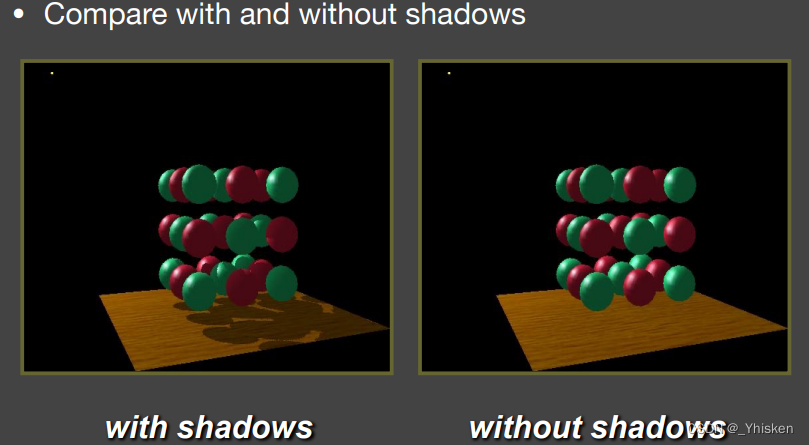
1.Self occlusion—自遮挡

自遮挡现象，如上图所示，地面上不仅有人物模型投射出的阴影，还有一圈圈的黑色纹路，而这是由于数值精度造成的问题。原因如上图右图所示：在光源的方向生成的Shadow Map是有一定分辨率的，也就是说在阴影图中记录的场景(此处为地面)的深度并不是连续的，而是形成了一个常数的阶梯过度的深度。简单的说在阴影图中，场景中的一片区域的深度都被认为成了是同一个值。而此时如果我们从摄像机出发到达另一个着色点连向光源得到距离d(如图中蓝色虚线所示)，显然这个d是比我们阴影图中的z要大的，也就是z<d，于是就产生了阴影，但是实际情况是根本就没有东西遮挡该着色点，于是就产生了自遮挡现象。从上面我们可以看到，光源方向如果越接近平行地面，那么自遮挡现象会更严重，而如果光照方向垂直于地面，那么问题则会减轻。

2.自遮挡的解决

1.Adding a bias

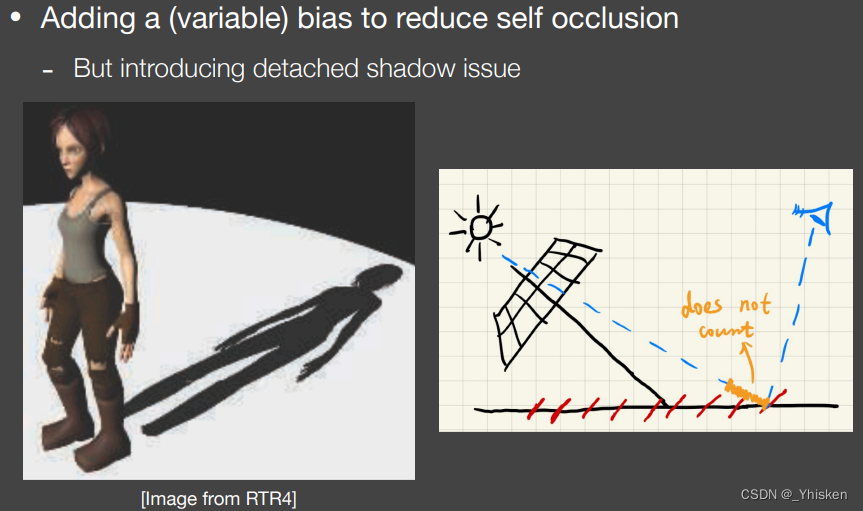
第一个方法，我们是加入了一个bias(图中橙色距离)，或者叫偏差量，宽容量。它的意义就是我们并不是判断z小于d而决定是否有阴影，而是z明显小于d，才判断它有阴影。当然，bias的值并不是固定的，我们上面说了，当光源方向和地面的夹角越小的时候，自遮挡现象越严重，那么我们就可以根据这个夹角动态调整bias的值，以达到动态减少自遮挡的目的。

虽然加入bias解决了自遮挡问题，但是它产生了新的问题，detached shadow，如上图左侧人物模型脚部的阴影丢失了。而当我们bias调的值过大的时候就会出现这种问题。

2.Second-depth shadow mapping*

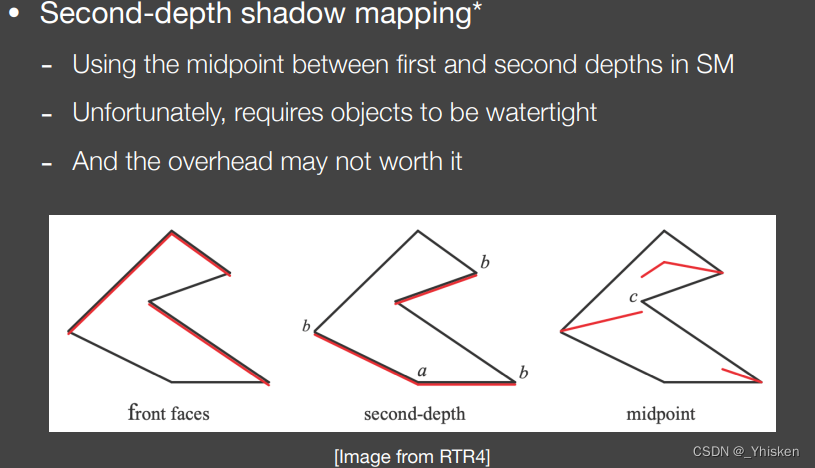
Second-depth shadow mapping和我们前面的SM不同，它生成的阴影图不再记录最浅深度，而是记录次浅深度(second-depth)，然后用它们两个去生成一个中间深度，用中间深度z'去和d比较，这种方法省去了bias。

当然这种方法同样存在问题，它只能描述watertight，也就是说所有的几何体都必须有正反面，就算是一个平面也需要做成很薄的box。同样它不能直接描述地板，但是可以通过把地板的次浅深度当成无限大就可以了。

其次的问题，如何记录最小和次小的深度呢？如果只是判断最小每次只和最小比较就可以了，但是如果要判断最小和次小就要多加入分支判断，虽然复杂度上没有变换，但是在实时渲染中对速度的影响是致命的。“RTR does not trust in COMPLEXITY—实时渲染不相信复杂度”

3.阴影的走样问题

阴影的走样问题本质上就是阴影图的分辨率不足的问题，我们前面也提到了，从光源得到的阴影图并不能完全表示连续的深度的过度和变化，所以自然就会有走样的问题产生。

工业界的做法大多采用Cascaded Shadow Mapping(简称CSM)，动态调整阴影图的分辨率来减弱走样效果。这里不过多介绍详情可以参考这位大佬写的文章：Unity实时阴影实现——Cascaded Shadow Mapping - 知乎 (zhihu.com)

三、The math behind shadow mapping

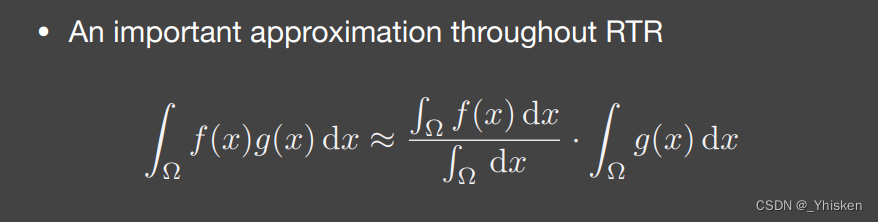
在微积分中有许多不等式，而在实时渲染中我们通常在特殊情况下把它们改成约等式来使用进行计算，如上图的两个函数的乘积的积分可以拆成两个函数积分的乘积(图中的分母为归一化常数)。

以上约等式在以下情况满足时更准确：1.g(x)的支撑集(这里可以简单的理解为实际的积分域)比较小的时候。2.g(x)在积分域内是光滑的，这里的光滑指的并不是连续，而是变化不大，比较低频的意思。

有了不等式我们就可以把它用在我们的渲染方程里，我们可以和容易的把visibility项拆分出来。得到的结果的右边就是直接得到的shading，乘上左侧的visibility则正是我们阴影图的原理。

同时我们说了，当函数积分线很小的时候，该约等式是比较准的，左侧比较小，那也就是小到一个点，一个Δ的时候，右侧表较小也就是小到一个点光源/方向光源的时候，这个时候是比较准的，这也就是SM做硬阴影的基础。

同时足够光滑的时候也就是对应了光照和BRDF是光滑的，光照是uniform的，例如各处radiance相同不变的面光源，BRDF则是diffuse的时候是光滑的，这个时候这个约等式也是相对准确的。

四、Soft Shadows—软阴影

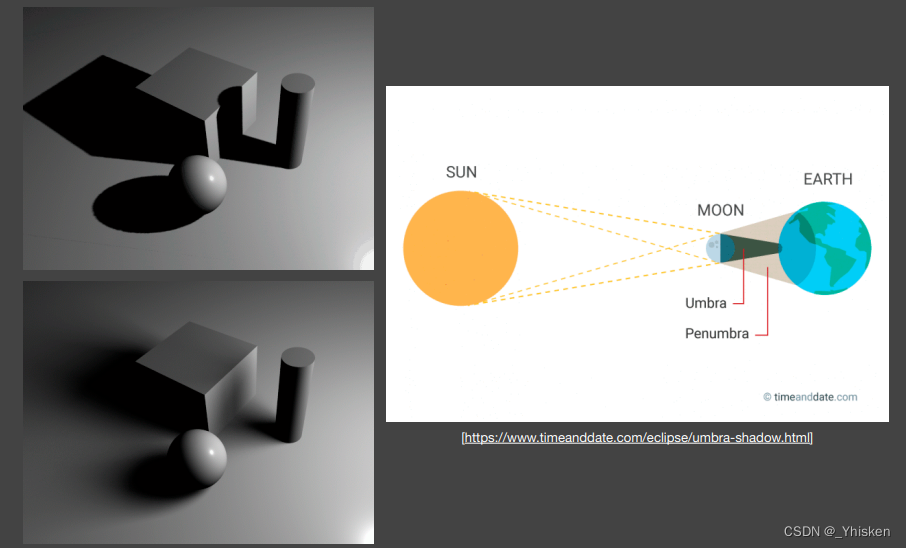
软阴影我们在光线追踪中说过，它更符合我们真实的世界，因为现实中没有绝对界限分明的硬阴影，所以我们来介绍如何得到实时的软阴影。

1.Percentage Closer Filtering (PCF)

PCF最开始是为了解决阴影的抗锯齿问题的方法，后来又被人们用来实现软阴影。那么我们先来说说人们是如何用PCF解决阴影锯齿的问题的。

Percentage Closer Filtering (PCF)，顾名思义就是一种滤波，我们在GAMES101中的反走样那节学过，滤波就是一种平均/模糊。但是注意，PCF并不是在最终的图像上对阴影进行模糊，也不是在阴影图中进行模糊，对走样的结果进行模糊是毫无意义的。

PCF的做法是在阴影图已经生成完毕和摄像机的图像中着色点进行比较的时候进行的，我们在对阴影图和相机图像对应着色点比较时得到的结果要么是在阴影中要么是不在阴影中，也就是说得到的值都是0和1，PCF时我们不再只考虑那一个像素的着色点，而是考虑它周围一圈的像素比如说是3x3，得到一堆0和1，然后对它们进行滤波操作。如上图例子得到的结果是0.667。

那么我们可以想象，当这个滤波足够大的时候，也就是阴影足够模糊的时候，它就变成了软阴影。

2.Percentage Closer Soft Shadows (PCSS)

那么通过上面我们知道了可以通过滤波的大小来调整阴影的软硬程度，那么阴影的每个位置都是一样“软”的吗？显然不是的，通过上图的钢笔在纸上的阴影我们知道，当阴影投射物(笔)和阴影接受物(纸)的距离越近的时候，阴影越硬，反之则越软。

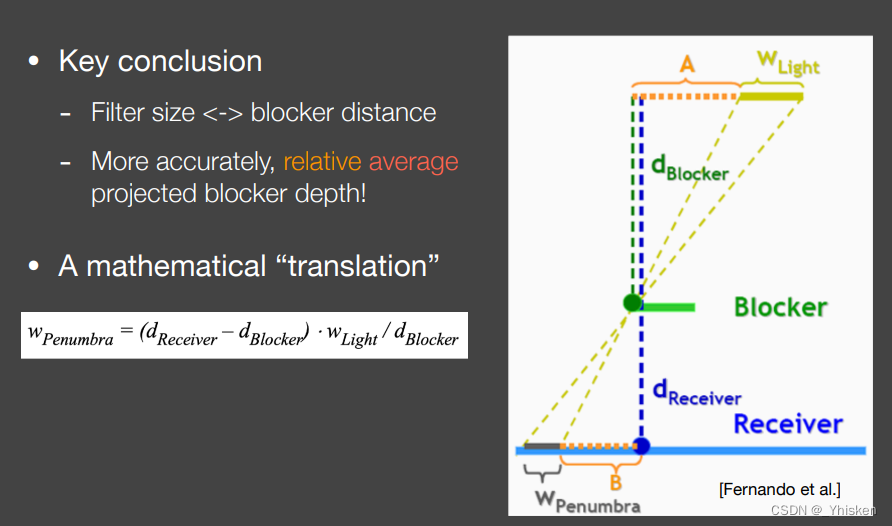
通过上面的思路我们就可以得到这么一个相似三角形，我们定义的Blocker就是遮挡物，我们还定义了它到光源的距离dB，而w决定了滤波尺寸的大小，通过相似三角形我们就可以得到w的计算公式，这也符合我们上面提到的投射物和接收物距离决定阴影软的程度的想法。

那么问题是通常阴影投射物不一定是平面，我们怎么确定Blocker distance也就是dB呢？这里我们同样的采取滤波的办法，对一定范围内的dB做滤波，得到该点的dB。

那么综上我们总结一下PCSS的完整步骤，首先得到阴影图中的所有Blocker的距离，也就是滤波过后的dB，然后我们通过dB得到每个比较结果处不同大小的滤波去对比较结果进行平均，再之后就和PCF的做法相同了。(注意，面光源实际上是得不到阴影图的，PCSS中是从面光源的中心点出发生成阴影图)

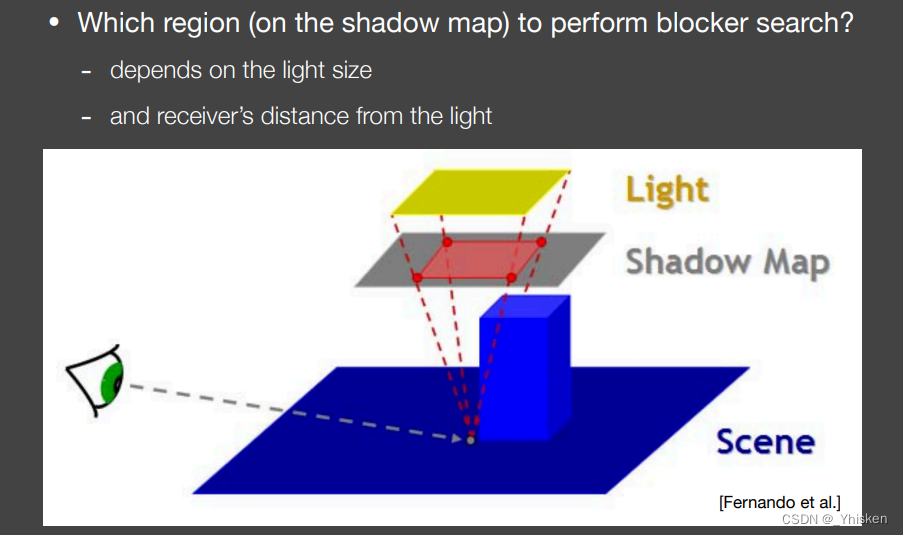
还有一个问题，我们说最开始计算平均dB的时候也要使用滤波，但是我们计算平均dB就是为了得到滤波的大小，这怎么办呢？有两种办法，一种方法就是最开始初始化一个固定的值，比如5x5。另一种方法，如上图所示，在光源和shadow map和着色点之间我们可以设置视锥体，shadow map假如设在前截面上，那么我们可以观察到，当光源距离Blocker的距离越远，光源越小的时候，滤波的尺寸越小。反之滤波则越大，我们会在更大的范围内搜寻Blocker的distance，这非常符合道理。

从头到尾，我们先在Shadow Map中进行比对找出在阴影中的点置成Blocker再对这些Blocker求平均的dB，求完dB我们再用dB决定PCF的大小然后对每个点都用PCF进行滤波平均操作。这样一套下来我们发现，要对纹理进行多次采样，性能开销很大，（同时如果是多光源，我们还要每个光源都生成一张阴影图，那就会更慢。）那么有没有方法可以加快这一过程的速度呢，答案是有，我们下一篇文章再聊。