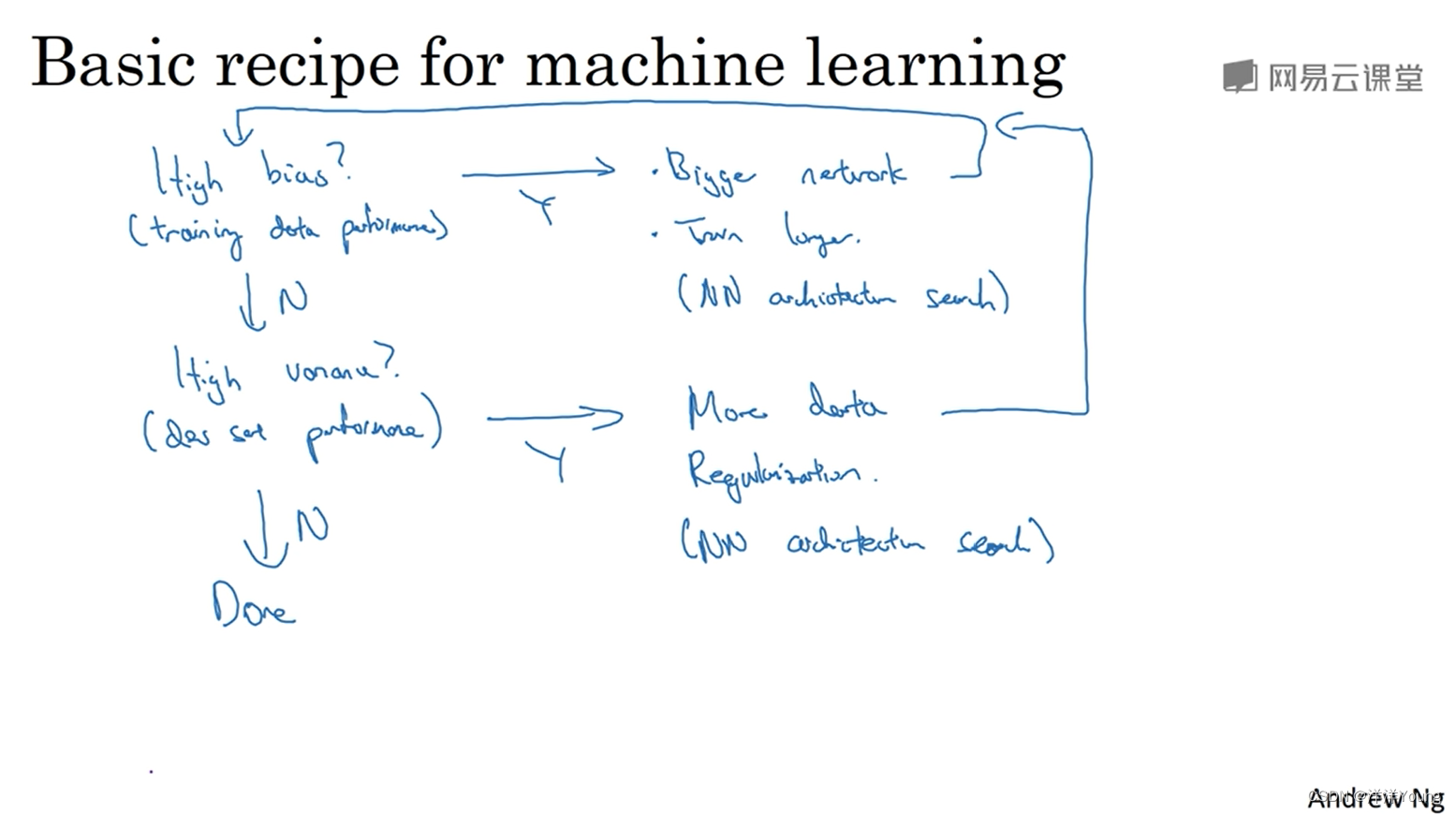
这个其实就是我们一致讨论的对偶映射，换了个马甲，差点认不出来了。本来是V->R

要变成U->R，就需要一个反向的V*->U*的映射。

 

注意这个式子，t属于U，phit转到了V，但是坐标也发生了变化，这是因为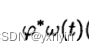 

 这是一个整体，实际上到右边后，w作用的是V上的变量，同时也必须是V上的坐标，那么原来的坐标就要通过切空间转换过去。

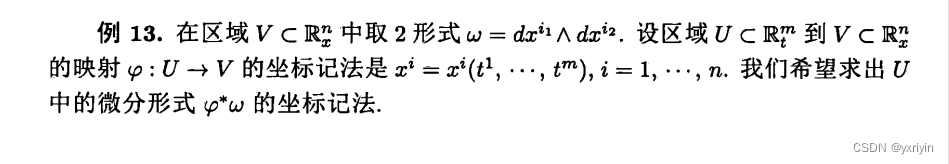
 这是一个很好的题目，首先2形式相当于微分dxdy，而U代表的是dt1,dt2...dtm,这样相当于问我们要怎么进行换元。

仔细看，首先是2个向量，有m个分量坐标，他们通过切空间可以转到V下。也是m个分量坐标。每个分量都是一个求和的式子。按照对偶公式：

 

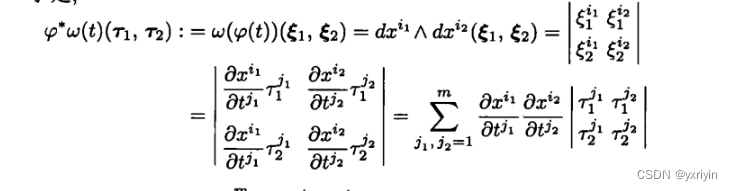
这一段只看计算的话就是这么回事。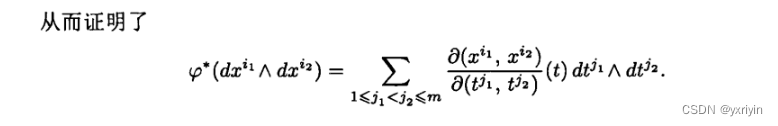 

 这就是换元的结论，考虑之前需要利用格拉姆矩阵，这里似乎更加清晰。

对于任意的dxdy，通过x=x(t1,t2....tm), y = y(t1,t2....tm) 就变成了一系列的求和，每个求和前面都是对应的偏导的雅克比矩阵的行列式的值。

没想到，直到这里，我们才获得了所有换元的具体方法。这也太复杂了吧。

 天哪，这里写了当维数相同的情况，就是查了一个雅可比行列式的值。

但还是留下了一个疑问啊，dxdy对应dt1,dt2,...dtm解决了。但是如果是dxdydz对应dt1dt2呢，按照上面的公式似乎是有问题的。等到后面积分再看吧。学无止境啊。

 

这个后面再看吧，不是非常重要。