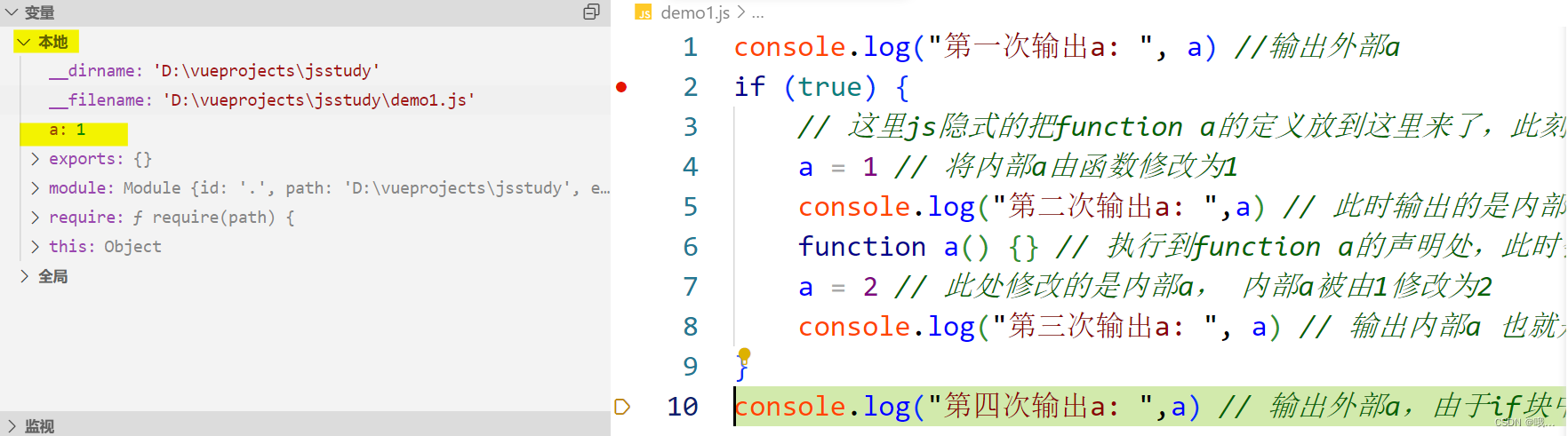
RSA的历史

RSA加密算法是一种非对称加密算法，在公开密钥加密和电子商业中被广泛使用。RSA是由罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）在1977年一起提出的。当时他们三人都在麻省理工学院工作。RSA 就是他们三人姓氏开头字母拼在一起组成的。来自RSA算法发表时的论文。

RSA计算过程

1、 N = P * Q （P和Q都是质数）
2、欧拉函数
    φ(N) = φ(P) * φ(Q) = (P-1) * (Q-1)
3、1< e <φ(N), 且e与φ(N)互质
4、(e * d) / φ(N) = K0…1
    d = (K0 * φ(N) + 1) / e

Bob 依照 步骤产生 N,e,d
     将 N,e发送给alice
     alice欲传送M给Bob
     M^e / N = K_1 … C
     C^d / N = K_2 … M

RSA计算实例

1、N = 5 * 11 = 55
2、φ(N) = (5-1) * (11-1) = 40
3、1 < e < 40 且e与φ(N) 互质 ，e = 7
4、 (e*d) / φ(N) = K_0 … 1
     d = (K_0 * 40 + 1) / 7
     K_0 = 4 ，d= 23

     Alice欲传送2给Bob
      2^7 / 55 = 2… 18
     18^23 / 55 = 74347713614021927913318776830 … 2

RSA时间复杂度

攻击者要破解C得到M，必须要知道d，攻击者只能拿到N、e、C
-> 要知道d，必须要知道φ(N)
-> 要知道φ(N),必须要知道P、Q
-> 要知道P、Q,必须要知道质因数分解N
-> 而质因数分解是NP问题(时间复杂度不是多项式时间，是指数时间复杂度)

RSA证明过程

欧拉定理
如果任何两个数M、N互质，那么
M^φ(N) - 1 = N的倍数
M^φ(N) = N的倍数+1

M^e = N的倍数 + C
C = M^e + (-N)的倍数
C = M^e + N的倍数
C^d = (M^e + N的倍数)^d
      = M^{ed} + N的倍数^d
      = M^{kφ(N) + 1} + N的倍数^d
      = M * M^{kφ(N)} + N的倍数^d
      = M * M^{φ(N)K} + N的倍数^d
      = M *(1 + N的倍数)^{k} + N的倍数^d
      = M + N的倍数