位运算专题

news2025/1/5 10:14:02

异或:相同为0，相异为1，无进位相加

约定:给定的所有数从左到右依次是从低位到高位，下标从0开始

一)给定一个数，判断它的二进制位表示中的第X位是0还是1

1)(N>>X)&1，先将x位右移动到最低位，然后再将这个数和1进行按位与操作，如果这个最低位是1，那么经过与1进行按位与结果就是1，如果这个X位是0，那么经过和1进行按位与结果就是0

二)为运算的优先级:能加括号就加括号，先运算的加上括号

三)将一个数N的二进制表示的第X位修改成1，其余位保持不变

四)将一个数N的二进制表示的第X位修改成0，其余位保持不变(必须让最终的数位的决定权在于原始的这个数)

五)提取一个数中二进制表示中最右侧的1:lowbit

N&(-N)

将N变成-N的操作是将N进行按位取反，然后再加1，

本质上就是将最右侧的1，(不包含这个1)左边的区域全部取反，最终结果就是N&(-N)

六)干掉一个数二进制中表示的最右侧的1(最低位的1变成0)

N-1本质上就是让最右侧的1(包含最右侧的1)右边的数全部按位取反，左侧保持不变

(因为从最低位0到最右侧的1区间之间减1减不动所以要进行借位)

N&(N-1)

一)只出现一次的数字

260. 只出现一次的数字 III - 力扣（Leetcode）

第一步:将数组中所有的元素进行异或操作，最终得到一个异或值，因为是不同的两个数字，所以说这个数字肯定不是0

第二步:取异或值最后一个二进制位是1的数，如果这个数是1，那么代表着这两个数字在这一位上不同，要么一个数字在这一位上是1，要么是一位数字在这一位上面是0

第三步:根据这一位上面的值进行分组，将这两个不同的数字分别分到两个不同的组上面，每一个组分别进行异或，最终两个组得到的值就是最终的结果

通过与这个 mask 进行与操作，如果为 0 的分为一个数组，为 1 的分为另一个数组。这样就把问题降低成了：“有一个数组每个数字都出现两次，有一个数字只出现了一次，求出该数字”，对这两个子问题分别进行全异或就可以得到两个解，也就是最终的数组了
class Solution {
    public int[] singleNumber(int[] nums) {
        int temp=0;
        for(int i=0;i<nums.length;i++){
             temp=temp^nums[i];
        }
        //1.得到temp,从而得到最终两个数异或的结果
//2.得到两个单身狗异或结果的值,在求出最低位是1的bit位的数值,根据这一位是1进行分组,两个组分别进行异或,最终两个组分别得到的数字就是最终的结果
        int bit=temp&(-temp);
        int[] dp=new int[2];
        for(int i=0;i<nums.length;i++){
            if((nums[i]&bit)==0) dp[0]=dp[0]^nums[i];
            else dp[1]=dp[1]^nums[i];
        }
    return dp;
    }
}
二)位1的个数:

191. 位1的个数 - 力扣（Leetcode）
public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int count=0;
     for(int i=0;i<=31;i++){
         if(((n>>i)&1)==1) count++;
      }
      return count;
    }
}
public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int count=0;
        while(n!=0){
            n=n&(n-1);
            count++;
        }
        return count;
    }
}
无符号右移:不论正负，高位均补0

右移:若正数，高位补0，负数，高位补1，一句话概括：高位补符号位
public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int count=0;
        while(n!=0){
            if((n&1)==1) count++;
            n=n>>>1;//左边只能补0
        }
    return count;
    }
}
三)比特位计数:

338. 比特位计数 - 力扣（Leetcode）

1)按位与操作:
class Solution {
    public int[] countBits(int n) {
        int[] array=new int[n+1];
       for(int i=0;i<=n;i++){
           int count=0;
           int temp=i;
           while(temp!=0){
               temp=temp&(temp-1);
               count++;
           }
           array[i]=count;
       }
       return array;
    }
}
2)动态规划:

2.1)首先定义一个状态表示:dp[i]表示i位置的数二进制1的个数

2.2)根据状态表示推到状态转移方程:

0->0000

1->0001

2->0010

3->0011

4->0100

5->0101

6->0110

dp[i]=dp[i>>1]+i&1
class Solution {
    public int[] countBits(int n) {
        int[] dp=new int[n+1];
        dp[0]=0;
        dp[1]=1;
//从左向右进行填表
        for(int i=1;i<=n;i++){
            dp[i]=dp[i>>1]+(i&1);
        }
    return dp;
    }
}
四)汉明距离:

461. 汉明距离 - 力扣（Leetcode）

思路:把两个数转化成二进制，看看两个数的二进制中有多少比特位不相同，根据异或运算的特性，相同为0，不同为1所以只需要统计两个二进制数异或的结果中有多少比特位是1即可
class Solution {
    public int hammingDistance(int x, int y) {
        int temp=x^y;
        int count=0;
        while(temp!=0){
            temp=temp&(temp-1);
            count++;
        }
    return count;
    }
}
五)判断字符是否唯一

面试题 01.01. 判定字符是否唯一 - 力扣（Leetcode）

解法1:哈希表

遍历这个字符串中的所有字符，如果这个字符在哈希表中没有出现过，那么直接存放到哈希表里面，如果这个字符已经在哈希表中出现过了，那么直接返回false

这里面的时间复杂度是O(N)，空间复杂度还是O(N)

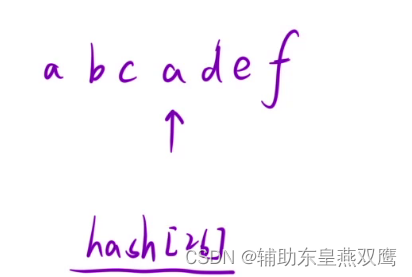
解法2:不需要创建一个真正的哈希表，使用字符数组进行代替即可hash[26]
class Solution {
    public boolean isUnique(String str) {
        char[] array=str.toCharArray();
        int[] countArray=new int[32];
        for(int i=0;i<array.length;i++){
            if(countArray[array[i]-'a']>0) return false;
            countArray[array[i]-'a']++;
        }
    return true;
    }
}