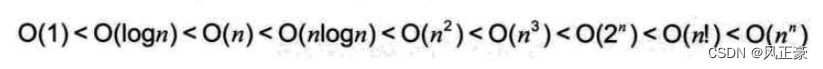前言
(1)因为上一篇博客:数据结构(2)—算法对于时间复杂度和空间复杂度计算的讲解太少。所以我在次增加多个案例讲解。
(2)上一篇已经详细介绍了,为什么我们的算法要使用复杂度这一个概念。因此,我这一篇将重点介绍,复杂度如何进行计算。
时间复杂度计算
(1)上一篇博客已经介绍了,一般情况下,我们是不会考虑空间复杂度的。所以我将会重点介绍时间复杂度的计算。
(2)我们之前说了,时间复杂度是采用的大O计法。(注:不懂的建议看上一篇的算法的时间复杂度部分,我已经介绍的很详细了)
(3)接下来我将直接上代码进行计算。我先贴代码,然后再讲解。如果感兴趣的,可以看代码自己先计算一边,然后再看解析。
示例1—入门训练
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{
for (int j = 0; j < N ; ++ j)
{
++count;
}
}
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}
(1)根据大O计法,我们知道,先要找到这个函数的具体执行时间。
(2)首先,我们看到两个for语句嵌套,第一个for语句里面需要执行N次,而第二个for语句嵌套在里面,所以最终的执行次数为N^2次。
for (int i = 0; i < N ; ++ i) //执行N次
{
for (int j = 0; j < N ; ++ j) //执行N*N次,所以最终结果是执行了N^2次
{
++count;
}
}
(3)第二个for语句里面没有嵌套,条件判断为 <2*N,而且每次自增为1。所以这里需要执行2N次。
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
(4)最后一个while中执行M次,M给定了一个常量10。所以这个while是执行10次。
int M = 10;
while (M--)
{
++count;
}
(5)综上所述,最终得出的结论是,这个代码执行次数如下
T ( n ) = n 2 + 2 n + 10 T(n)=n^{2} + 2n +10 T(n)=n2+2n+10
(6)而根据大O计法,可知,当f(n)为n^2。n趋向于无穷大,最终T(n)/f(n)为常数。所以时间复杂度为O(n ^ 2)。
(7)总结,大O计法就是保留代码执行字数的最高项。
示例2—最高项的常数不唯一
void Func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}
(1)同理,先计算出这个函数总体执行次数。
(2)第一个for循环,判断条件为 k < 2 * N,K每次自增为1,所以需要执行2N次。
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
(3)同理,这个while固定执行10次。
int M = 10;
while (M--)
{
++count;
}
(4)所以,这个函数最终执行的次数为 2N+10。那么根据大O计法,这个时间复杂度难道是O(2N)?
(5)看到我这么说,那么答案肯定不对。大O计法规定了 ,如果最高项的常数不是1,则需要去除最高想的常数。比如,此题的最高项为N,他的常数为2,所以这一题的时间复杂度为O(N)。
示例3—出现多个变量
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++ k)
{
++count;
}
for (int k = 0; k < N ; ++ k)
{
++count;
}
printf("%d\n", count);
}
(1)这个题目,我们会发现有两个变量,那么时间复杂度怎么进行计算呢?其实也没有想象的那么复杂,只需要按情况分析即可。
(2)第一,假设N和M差不多大小,那么时间复杂度就是O(N+M)。
(3)第二,假设N远大于M,那么时间复杂度就是O(N)。
(4)第二,假设N远小于M,那么时间复杂度就是O(M)。
示例4—执行次数唯一
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++ k)
{
++count;
}
printf("%d\n", count);
}
(1)我们看这个函数,会发现,传入形参N是没有被使用到的。也就是说,这个函数固定运行100次。
(2)对于这种情况,可能有些人就有点懵了。那么他的时间复杂度是多少呢?
(3)大O计法规定了,如果是固定了执行次数的函数。时间复杂度为O(1)。
示例5—执行次数存在多种情况
const char * strchr ( const char * str, int character )
{
while(*str != '\0')
{
if(*str == character)
{
return str;
}
str++;
}
return NULL;
}
(1)首先说明一下这个函数的作用。假设我们有一个字符串"sdyzscx",我要找到这个字符串的字符’y’,那么他将会遍历这个字符串。如果找到了字符’y’,将会返回该字符的位置。否则返回一个空指针。
(2)这个题目,我们会发现,很难找到他的具体运行时间。因为假设我们要寻找的字符永远是字符串的第一个,那么这个函数的执行字数永远是1,那么时间复杂度就是O(1)。我们将这种情况称之为,最好情况。
(3)但是假如我们每次要寻找的字符总是出现在中间位置,也就是只要执行N/2次。这种叫做平均情况。
(4)最后一种,就是我们保持绝对的悲观态度,假设我们寻找的字符永远是字符串最后一个字符,或者找不到。那么执行次数为N,时间复杂度为O(n)。这种叫做最坏情况。
(5)在实际中,一般我们都是关注的最坏运行情况,所以此题的时间复杂度为O(n)。
示例6—执行次数不直观
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
(1)这就是一个冒泡排序算法,但是我们会发现,这个题目的似乎运行次数不太好进行计算。这个时候,最好的方式是带入具体数值。
(2)假设n为10,传入的数组元素有10个。
<1>第一次运行,第一个for语句进入判断,第二个for语句的判断end就是10。所以这里是执行9次。
<2>第二次运行,这个时候,end为9了。那么第二个for语句就是执行8次。
<3>依次类推,我们可以知道,这里就是执行了9!(注意’!'表示阶乘的意思,不明白的可以看看高中课本)。
<4>如果将具体数字转换为变量n,就可以得出,这个函数实际上执行次数为:(n-1)! 根据小学的知识,我们可以知道,执行次数为
( n − 1 + 1 ) ( n − 1 ) ) 2 = n 2 − n 2 \frac{(n-1+1)(n-1))}{2}=\frac{n^{2}-n}{2} 2(n−1+1)(n−1))=2n2−n
<5>根据大O计法可知,最终的时间复杂度为O(n^2)
示例7—二分查找的时间复杂度
/* 作用:二分查找,用于寻找有序数组的值
* 传入参数 :
* a : 有序数组的首元素地址
* n : 该元素的长度
* x : 要查找的元素
* 返回值 : 如果找到了元素,返回该元素在数组的第几项。没有找到元素,返回-1。
*/
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n-1;
while (begin < end)
{
int mid = begin + ((end-begin)>>1);
if (a[mid] < x)
begin = mid+1;
else if (a[mid] > x)
end = mid;
else
return mid;
}
return -1;
}
(1)这个函数就是一个有序数列的二分查找函数。
(2)看到这个函数,依旧是没有任何思路的,所以还是直接套数字。假设有一个数列[0,1,2,3,4,5,6,7,8,9],因为计算时间复杂度是按照最坏的条件来进行计算,所以假设我们需要找到的数字为0。
<1>首先,传入这个数组,begin为0,end为9(注意,end为9,但是是指向的数组的最后一个元素,因为数组的第一个元素从0开始)。mid=(9-0)>>1 =4,所以min指向元素4。
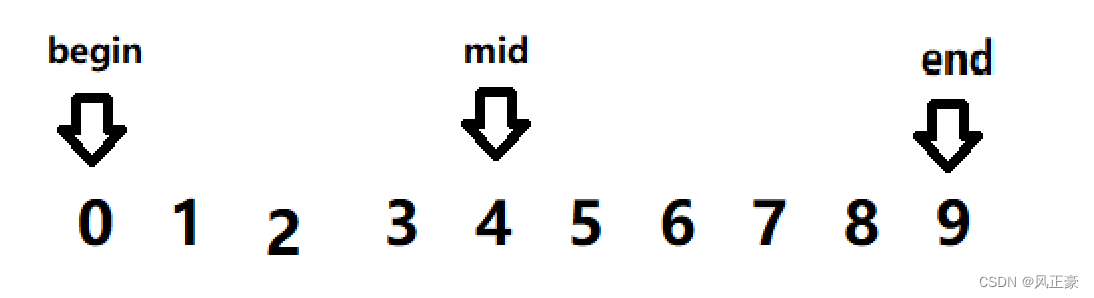
<2>我们会发现0是小于4的,所以end=mid=4。mid=0+(4-0)>>1=2。
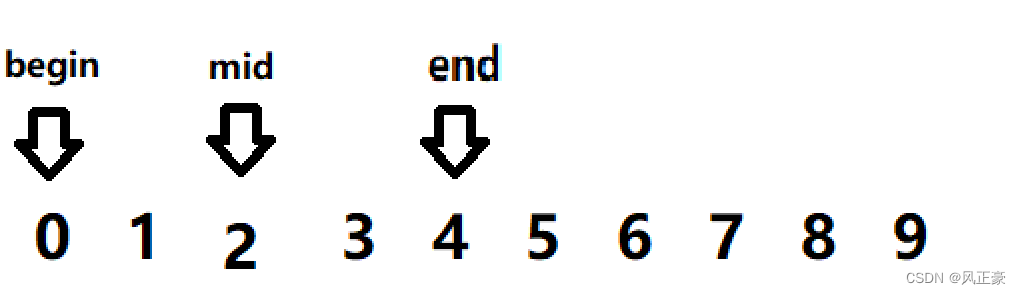
<2>这个时候,我们依旧会发现0是小于2的,所以end=mid=2。mid=0+(2-0)>>1=1。
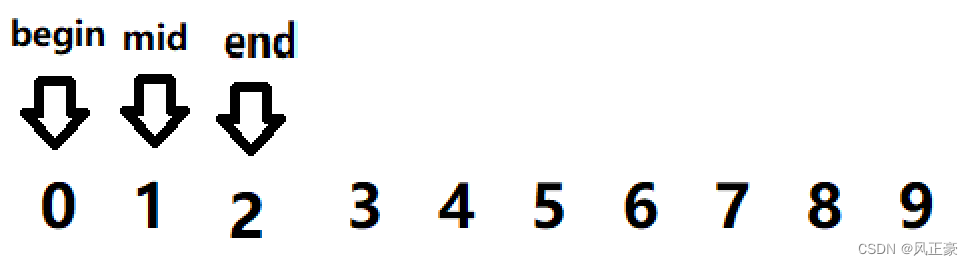
<3>0是还是小于1的,所以end=mid=1。mid=0+(1-0)>>1=0。
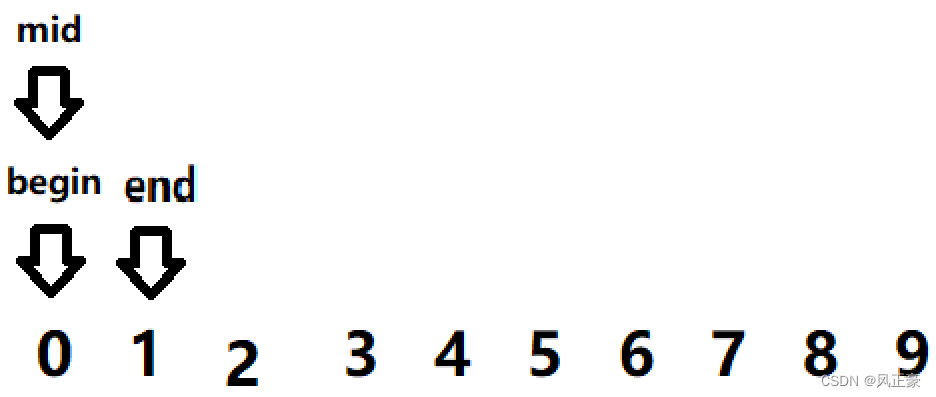
<4>最后,我们会发现a[mid] == 0,值返回。
(3)
<1>根据上面这个例子,我们会发现,最坏情况需要运行4次。
<2>所以,我们假设一个有序数组有N项,由于我们按照最坏的情况进行讨论,所以每次寻找,就排除了1/2的数据。
<3>第一次寻找,还剩下N/2项,
<4>第二次寻找,还剩下N/4项。
<5>依次类推,我们假设最坏的情况是找了X次。那么最终满足条件2^(X-1)<N<2 ^X,那么X就找到了。
<6>因此,时间复杂度满足如下公式,但是很少部分时候,有些数据结构的书中,写成后面这个式子。(注意,与数学的写法不同!不严谨但是很多时候当成是等于)
O ( l o g 2 N ) = O ( l g N ) O({log_{2}}^{N}) = O(lg_{N}) O(log2N)=O(lgN)
示例8—递归调用函数的时间复杂度
long long Factorial(size_t N)
{
return N < 2 ? N : Factorial(N-1)*N;
}
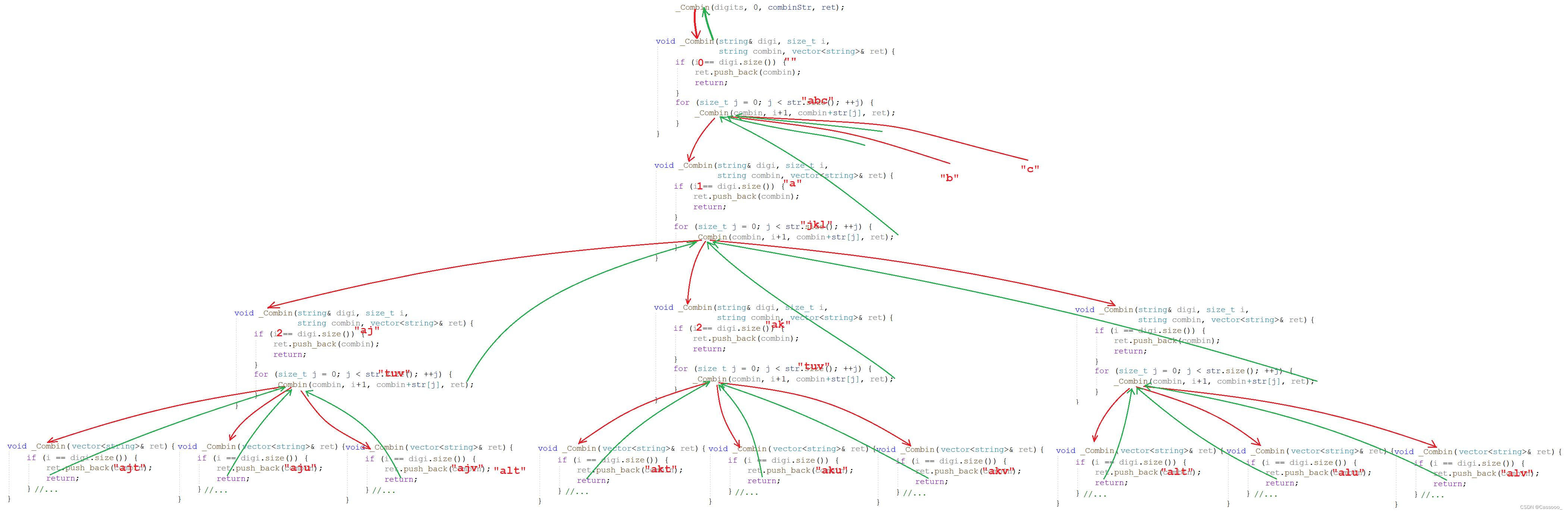
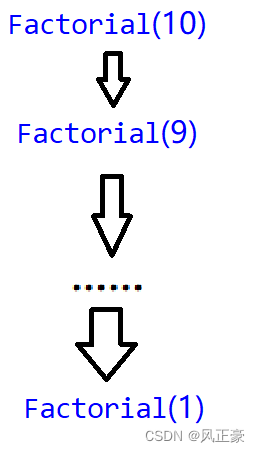
(1)这个依旧无法直接看出结果,依旧套具体数值来寻找思路。假设N为10。那么他的函数调用关系如下。
(2)我们会发现,传入的N为多少,那么执行的次数就是多少。所以时间复杂度为O(N)。
空间复杂度计算
示例1—初级训练
(1)看了上面这么多例子之后,我们对时间复杂度的计算应该还是比较了解了。那么如何计算空间复杂度呢?拿下面这个例子开始计算。
(2)空间复杂度也是采用的大O计法,首先我们先数一下下面这个函数中,建立了多少个变量。
(3)我们看到,这个函数中就只建立了一个变量exchange ,但是这个exchange 是在for循环里面的,那么这个函数的空间复杂度就是O(N)吗?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
(4)答案是错误的,因为数据结构中,时间是累积的,空间是不累积的。可能有些人看到这句话,就蒙圈了。什么意思呢?
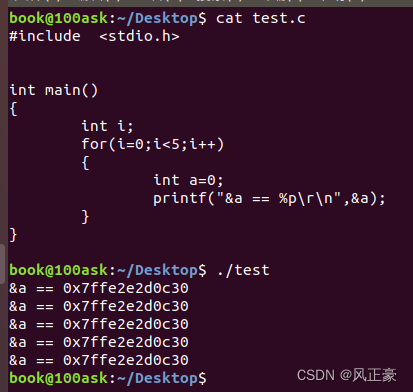
(5)首先我们得知道,exchange 这个变量虽然是在for循环中,但是每次for循环不会都创建一个exchange 变量,而是重复利用同一个空间。如下图,因此,这里的空间复杂度为O(1)。
示例2—递归调用的空间复杂度计算
long long Factorial(size_t N)
{
return N < 2 ? N : Factorial(N-1)*N;
}
(1)根据上面的知识之后,那么这个函数的空间复杂度是多少呢?
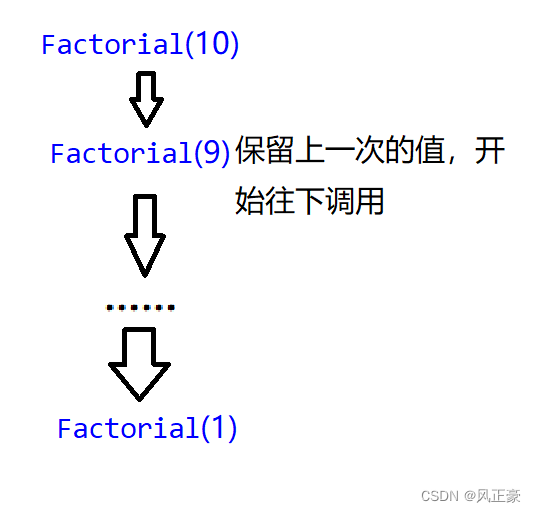
(2)答案很简单,为O(N)。为什么呢?因为在递归调用的时候,每一次函数调用,都会保留上一次的值。
(3)而最终调用到Factorial(1)的时候,结束函数调用,开始返回,就开始销毁之前的变量。

示例3—malloc函数的空间复杂度计算
long long* Fibonacci(size_t n)
{
if(n==0)
return NULL;
long long * fibArray =(long long *)malloc((n+1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; ++i)
{
fibArray[i ] = fibArray[ i - 1] + fibArray [i - 2];
}
return fibArray ;
}
(1)这是一个斐波那契数列,这个空间复杂度是多少呢?
(2)其实对于这种空间复杂度和时间复杂度计算,最重要的是看这个函数与传入参数有没有关系。如果没有关系,那么大概率是O(1)。有关系,就只需要看有关系的那一部分。
(3)我们会发现,这个函数,只有malloc函数与传入参数n有关系,所以其实我们需要看malloc那一句话。因为malloc申请到的数据为n+1,所以这个函数的空间复杂度就是O(N),其他地方根本不需要看。
总结
(1)时间复杂度和空间复杂度都是采用的大O计法。复杂度计算只需要看与函数传入参数有关系的部分。
(2)时间复杂度要点:
<1>只需要看最高项。
<2>最高项的常数可以忽略。
<3>时间复杂度一般只看最坏情况。
(3)空间复杂度要点:
<1>时间是累积的,空间是不累积的。
<2>一般情况,我们只考虑时间复杂度,不考虑空间复杂度。
(4)根据复杂度,我们可以很好的衡量一个算法的优缺点,不同时间复杂度的执行时间由小到大。