二叉树遍历非递归算法
文章目录
- 二叉树遍历非递归算法
- 二叉树的遍历
- 一、先序遍历非递归算法
- 算法构思:
- 从先序遍历的递归算法得出循环算法的思路:
- 下面进行框架构建:
- 代码实操:
- 二、中序遍历(左-根-右)非递归算法
- 中序遍历二叉树的过程
- 构建思路:
- 根据以上思路,构建规范框架:
- 代码框架:
- 代码实操:
- 三、后序遍历(左-右-根)非递归算法
- 构建思路:
- 代码框架:
- 代码实操:
- 四、例子:路径之逆
- ♥ 问题:
- 解:
二叉树的遍历
•三种遍历
• 先序遍历: 根节点–>左子树–>右子树
• 中序遍历: 左子树–>根节点–>右子树
• 后序遍历: 左子树–>右子树–>根节点
•两类算法
• 递归算法(具体看我上一篇文章)
♥直观,易读
♥效率低下
• 非递归算法
♥ 如果一个算法可以使用递归或循环来进行完成,在不影响代码阅读的情况下,可以使用循环,来降低复杂度。
下面介绍二叉树的遍历,把递归遍历用循环遍历代替:
一、先序遍历非递归算法
算法构思:
我们既然要先序遍历二叉树,就要先了解如何先序遍历二叉树
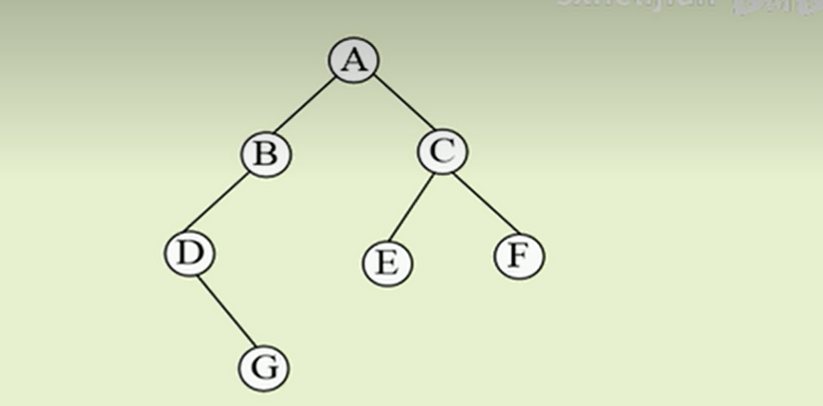
• 先序遍历:
根节点–>左子树–>右子树 : A BDG CEF
▪ 先序遍历二叉树的过程
•访问根节点
• 然后先序遍历左子树
• 最后先序遍历右子树
构建思路 :
先遍历根节点 , 然后再遍历其左子树和右子树,这是一个层级,把其左子树或右子树再次当做一个独立的树去调用(每个节点被传入调用的时候,都当了一次根节点,所以才有机会被输出),目的就是输出访问一遍.
从先序遍历的递归算法得出循环算法的思路:
通过观察先序遍历,我们先遍历输出根节点, 在这一个层级内,我们接下来是去遍历处理左子树, 处理完之后,再去遍历处理右子树。递归调用,当然容易理解,但是此时要去用循环来按照递归的顺序方法输出,并且按照循环的方式来进行。

我们现在去用人脑来进行遍历,先遍历 A , 输出A之后,此时当时我们当然要去处理左子树,但是后续我们怎么去处理右子树呢?
所以我们需要做标记,怎么做标记呢?当然是先将根A的右孩子 C 入栈,以便后续处理完左子树之后,再出栈右孩子,进而处理右子树。
根据栈的特性,先进后出, 后进先出 , 我们处理完根之后, 要先处理左子树,但是后续我们还要处理右子树,为了避免找不到右子树的信息,所以根节点处理完后,先把右孩子入栈,
然后再把左孩子入栈。此时栈顶是根节点的左孩子,所以我们可以先处理左孩子了,根据先序遍历的规则,我们再结合递归的思想,用循环代替的话,栈顶的节点也可以看做一棵子树的根,我们就可以出栈此节点,然后再接着遍历其孩子,每一个层级都是有先后顺序的。等左子树处理完,栈里就剩一个根节点的右孩子,我们就可以将其出栈,并处理右子树了。就这样环环相扣,循环的好处是,省去了递归每次保存临时变量和其他现场的步骤,一定程度上提高了效率。
下面进行框架构建:
♥算法步骤:
if(当前b树不空)
{
根节点b进栈;
while(栈不空)
{
出栈节点p并访问之;
若*p节点有右孩子,将其右孩子进栈;
若*p节点有左孩子,将其左孩子进栈;
}
}
代码实操:
//传入二叉树
void PreOrder1(BTNode *b)
{
//定义存储数组栈,用来调剂各个节点的访问顺序
BTNode *St[MaxSize];
//定义指针p来进行对节点进行操作和访问
BTNode *p;
//栈顶初始为-1
int top=-1;
//先让根节点入栈,栈顶累加
top++;
St[top] =b ;
//接下来就是为了先序遍历二叉树循环处理二叉树了
//栈不为空时循环
while(top>-1)
{
//根节点已经入栈,我们先处理根节点,所以退栈并访问之
p = St[top];
top--;
printf("%c",p->data);
//接下来就是处理本层级的左子树和右子树了
//由于是先序遍历,所以先处理完左子树,再处理右子树
//根据栈的特性,先进后出,所以右子树后处理,所以先把根节点的右孩子入栈
if(p->rchild!=NULL)
{
top++;
St[top]=p->rchild;
}
//下面我们就可以遍历左子树了
//根据栈的后进先出特性,此时如果存在左孩子,就将其入栈
//当接下来循环回去的时候,我们就可以再次此层级的左孩子当做左子树的根,进行访问
if(p->lchild!=NULL)
{
top++;
St[top]=p->lchild;
}
}
}
二、中序遍历(左-根-右)非递归算法
中序遍历二叉树的过程
• 中序遍历左子树
• 访问根节点
• 中序遍历右子树
构建思路:
我们要用循环来代替递归,所以我们就要深入进入,看如何去中序遍历二叉树了.

我们既然要左-根-右去访问二叉树,所以就需要先处理左子树,但是我们能直接处理左子树的根节点吗?当然是不能的,我们根据递归的思想,左子树依然是一棵树,当其存在左孩子的时候,我们能坐视不管,直接访问根节点吗?当然是不能的,所以我们需要顺着根节点的左孩子这一条枝,一直走,直到走到有一个节点,其没有左孩子了,我们此时才能将其作为我们的第一个遍历的节点.
我们可以去思考,此节点在同一层次是属于根或左或右节点呢? 其没有左孩子了,我们才将其作为第一个节点来访问,说明当一个节点没有左孩子的时候,我们不得不去访问此层次的根节点了,根据先序遍历,访问完根节点,接下来是访问其右孩子。如果此时其右孩子没有子孙了,才能断定此层已经遍历完,下面该访问上一层级的根节点了(因为此时我们这一层级处理完之后,根据先序遍历的递归处理思想)我们相当于是处理完了上一级的根节点的左子树,接下来才该处理上一层级的根节点,然后是右节点,以此类推。
根据以上思路,构建规范框架:
(1)所有左下孩子进栈,体现先访问左子树的特点。
(2)当所有左下孩子进栈后,栈顶节点p没有左孩子(即没有左子树)或者其左子树均已访问,所以可以访问p节点.
(3)当访问p节点后,转向其右孩子,采用同样的方式中序遍历右子树.
(4)我们左孩子先入栈是为了后续按照层次进行访问, 当其左子树处理完之后,才可以处理栈顶元素
代码框架:
if(当前b树不空)
{
p=b;
while(栈不空或者p!=NULL)
{
while(p有左孩子)
{
将p进栈;
p=p->lchild;
}
if(栈不空)
{
出栈p并访问之;
p=p->rchild;
}
}
}
代码实操:
//传入要遍历的二叉树
void InOrder(BTNode *b)
{
//因为要分层次进行处理,需要用到数组栈结构
BTNode *St[MaxSize];
//定义操作节点的指针
BTNode *p;
//初始化栈
int top=-1;
//先传入树根,树根是联系此二叉树的根
p = b;
//下面开始进行中序遍历
//当栈里不空,或者传入的树不空,那就接着进行遍历
while(top>-1 || p!=NULL)
{
//上面思路讲的很清楚,要分层次遍历,中序遍历是左-根-右,所以直到节点没有左孩子
//我们才能访问此节点,因为根据递归的思想,在同一层次,是左-根-右,此时没有左孩子,才能访问根
//我们按层次,先将根的左孩子依次入栈,当一层一层处理,当处理完本层,也相当于处理完了上层的左子树,才能处理上一层的根
while(p!=NULL)
{
//将所有左下孩子进栈,直到遇到没有左孩子的节点
top++;
St[top]=p;
p = p->lchild;
}
//此时上一层循环跳出,p此时指向的那个节点没有左孩子
//所以此时应该出栈的节点就是栈顶节点
//如果此时栈里还有节点,那我们就出栈
if(top>-1)
{
p = St[top];
top--;
printf("%c",p->data);
//出栈完此层的根节点,根据中序遍历规则,我们当然是去处理其右孩子
p = p->rchild;
}
//如果此节点只有一个右孩子,右孩子没有子孙
//循环上去的时候,我们把其右孩子入栈,然后判断出右孩子没有左孩子,就跳出循环,
//然后就访问此节点,再发现其没右孩子,就说明这一层已经完成,也说明上一层级的左子树访问完了
}
}
三、后序遍历(左-右-根)非递归算法
后续遍历二叉树的过程:
先访问左子树,再访问右子树,最后处理根
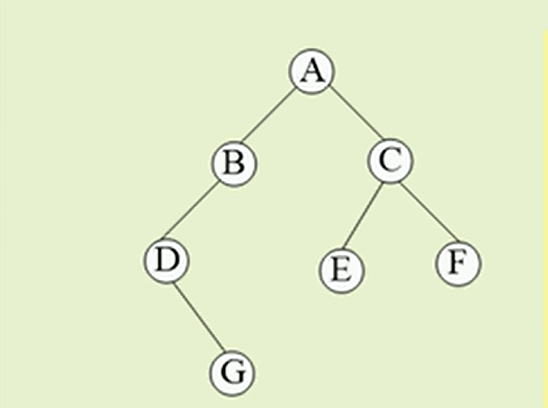
构建思路:
我们依然是先遍历左孩子,此时我们传入树b ,然后我们此时先遇到是是A, 此时A是树根,不能先处理,因为其左子树还未处理,所以先将A入栈,接着B也入栈,D入栈,此时判断到D没有左孩子,因为我们遍历的顺序是左-右-根, 此时其没有左孩子,所以在这一层级内, 此时D作为此层级的根, 需要先访问其右孩子G , 然后再访问此层级的根节点D, 此时我们的逻辑是没有问题的 .
但是我们会注意到, 我们访问了两次D ,
• 一次是第一次访问到D ,D由于是作为根节点,所以需先访问其右孩子G
• 第二次是访问完G之后, 需访问此层级的根节点D了
但是我们如何判断我们是第一次访问到D ,还是第二次访问到D ,这两次的操作是不同的,所以我们需要从中提取规范性或标志性的信息,从而去让代码去做对应的操作.
难点:
▪ 如何判断一个节点* b 的右孩子节点已访问过
条件:
▪ 在后续遍历中,*b的右孩子节点一定刚好在 *b之前访问.
方法:
▪ 用p保存刚刚访问过的节点(初始值为NULL);
▪ 若 b->rchild == p 成立,说明这是第二次访问到*b, 说明 *b的左右树均已访问,现应访问 *b.
代码框架:
if(当前b树不空)
{
do
{
while(b!=NULL,b有左孩子,将进栈)
出栈节点b(出栈不代表访问,出栈是要操作以此节点为根的层级了);
if(b的右子树已访问)
则访问b并退栈
else
b = b->rchild;
}while(栈不空);
}
代码实操:
//传入要后序遍历的二叉树
void PostOrder1(BTNode *b)
{
//为了每一层级有序遍历,定义数组栈,进行记录每层的顺次
BTNode *St[MaxSize];
//处理节点的指针
BTNode *p;
//栈初始化
int top=-1;
//注意:此时进行的是左-右-根,此时不能将树根入栈
//当传入的树不为空,则进行遍历
if(b!=NULL)
do
{
//将根节点的所有左节点进栈,方便后续进行层次遍历
while(b!=NULL)
{
top++;
St[top]=b;
b=b->lchld;
}
//此时*b指向的节点没有左孩子的时候,说明就该处理此时以*b为根的层级的右孩子了
//在此层级内,我们此时还未访问遍历节点,所以此时标志已访问的上一个节点的 p置空
p = NULL;
/** _____________
注意:此时引入的p,我们要知道p的作用是什么?是标志此层级,右孩子是否已经访问过
所以,如果此层级一旦结束,那么p就要置空了,我们需要在每次第一次访问同一层级的根节点前
将p置空,以免影响不同层级的判断,所以我们就要保证我们在结束一个层次后,进行跳出置空p
**/
//经过上面循环的过滤,说明此时b所指向的左子树为空,或者已经处理完了
flag = 1; //表示*b的左子树已经访问或空,下面该处理此层级的右子树了
//当栈里不为空或左孩子已经处理完,我们就继续处理此时*b为根节点的右孩子了
while(top!=-1 && flag==1)
{
//栈顶元素即为*b
b=St[top];
//下面开始处理*b节点,分两种情况
//此时以*b为根的层级,左孩子为空或已经处理完了,该处理右孩子了
//但是我们需要判断这是已经处理完右孩子或下一步该处理右孩子了
if(b->rchild == p) //如果刚才遍历的就是*b的右孩子,说明该遍历根*b了
{
//我们此次访问*p,可以理解成上一步已经处理完右孩子了,这次该处理此层级的根了
//同时我们也可以理解成, 什么时候,需要强制输出一个数
//在同一层级遍历,当一个节点,没有左孩子,没有有孩子了,当然要强制输出此层级的根节点了
//所以第一次输出的必然是,在递归思想内,被单独当做根的节点被输出,我们在跳出或初始化的时候,已经将上一个访问节点置空
//并且当我们进行回溯输出的时候,不会跳出循环的,因为右孩子是没有子孙的,上一次访问也是空,正好符合输出条件。
pirntf("%c",b->data);
top--;
p = b;
}
//或者是第一次访问b,该处理右孩子了
else
{
//此时作为单独的右孩子,或许应该被输出,但是如果右孩子是右子树呢?
//我们就需要将其重新看成一个子树进行处理对待,进行分层遍历,所以我们需要跳出此循环
//我们可以定义一个标志flag, 表明我们此层级已经完成了,需要进行下一层的进栈和访问了
b = b->rchild;
//标志跳出循环,该处理以b为根的层级的左子树了
flag = 0;
}
}
}while(top!=-1);
}
/*
最好能走一遍,这样更能理解递归思想,用循环实现递归,牺牲了代码的可读性
/*
四、例子:路径之逆
♥ 问题:
二叉树采用二叉链存储结构,设计算法输出从根节点到每个叶子节点的路径之逆
解:
采用后续遍历非递归算法,遍历到叶子节点的时候,恰好符合从叶子结点到根节点。
试想一下,后序遍历是左-右-根,
回想后序遍历,当我们不得不输出访问节点时,我们访问的顺序数左-右-根,不得不输出的时候是左右节点都是空,只有根,所以在这一个层次中,我们只能输出此层次的根,此时输出的是二叉树的叶子.
所以我们只需要通过后序遍历的方法,在访问节点的时候,加一个判断是否是叶子节点的判断即可。
代码构思:
void AllPath(BTNode *b)
{
BTNode *St[MaxSize];
BTNode *p;
int flag,i,top=-1;
if(b!=NULL)
{
do
{
//将*b所有左节点进栈
while(b!=NULL)
{
top++;
St[top]=b;
b=b->lchild;
}
p=NULL;
flag=1;
//当栈非空处理每一个叶子节点
while(top!=-1&&flag)
{
b = St[top];
//加判断
if(b->rchild == p)
{
if(b->lchild == NULL && b->rchild == NULL)
{
//若叶子,输出栈中所有节点值
for(i=top;i>0;i--)
{
printf("%c->"St[i]->data);
}
printf("%c\n",St[0]->data);
}
top--;
p=b;
}
else
{
b = b->rchild;
flag = 0;
}
}
}
while(top!=-1);
printf("\n");
}
}










![[附源码]Python计算机毕业设计SSM基于数据挖掘的毕业生离校信息系统(程序+LW)](https://img-blog.csdnimg.cn/943f15acc0774605920744688d73c9c0.png)