基于牛顿方法在直流微电网潮流研究（Matlab代码实现）

news2025/1/12 22:56:16

💥💥💥💞💞💞欢迎来到本博客❤️❤️❤️💥💥💥
🎉作者研究：🏅🏅🏅本科计算机专业，研究生电气学硕。主要研究方向是电力系统和智能算法、机器学习和深度学习。目前熟悉python网页爬虫、机器学习、群智能算法、深度学习的相关内容。希望将计算机和电网有效结合！⭐️⭐️⭐️
🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者，方便大家进行学习！亲民！！！

📋📋📋本文目录如下：⛳️⛳️⛳️

目录

1 概述

1.1 直流电网中的潮流

1.2 创新点和相关工作

1.3 本文结构

2 数学/网络模型

2.1 主-从操作

2.2 孤岛运行

3 牛顿法

4 案例及Matlab代码实现

4.1 算例

4.2 实现结果

4.3 分析

5 Matlab代码实现

1 概述

潮流是一个非线性问题，需要用牛顿法求解具有恒定功率端子的直流微电网。本文提出了牛顿法在此类网格中二次收敛的充分条件。经典牛顿法以及近似牛顿法在主从和孤岛操作中都进行了分析，并带有下垂控制。提出了从接近 1 pu 的电压开始的收敛性以及解的存在性和唯一性的要求。计算结果补充了这一理论分析。

微电网有望在未来的智能电网概念中发挥基本作用。特别是直流微电网，由于其在效率、可靠性和可控性方面的优势，正获得越来越多的关注。直流微电网由于没有无功功率或频率控制，因此可以实现高效率和简化控制；由于具有孤岛运行的能力，因此可以实现高可靠性；由于许多发电和存储技术已经是直流的（如太阳能光伏发电、电池），因此可以实现简单的集成。此外，大多数家用电器可以适应直流操作。在一个典型的直流微电网中，电力电子转换器可以作为恒定电流或恒定功率运行。在后一种情况下，电网的模型变成了非线性的，需要用功率流算法进行静止状态分析。这个问题是非线性/非凸性的，需要用数值算法来解决。当然，由于问题的非线性性质，这类算法的收敛性并不总是得到保证。一个算法甚至可能发散或趋向于一个不现实的解决方案。

因此，有必要建立精确的条件，要确定潮流算法收敛到独特且现实的解决方案的确切条件。另一方面，直流微电网有两种主要的控制方式，即主从控制和垂流控制。

在主从控制中，转换器固定整个电网的电压；这是并网微电网最常见的操作。

对于孤岛模式操作，电网中的功率通过下垂控制进行修改，以实现稳定的平衡点。

两种操作模式都需要潮流算法。重要的是要注意交流电网中存在线性化，也称为直流功率流。该名称来自于交流电网中的角度与线性直流电网中的电压之间的类比。本文与这些类型的类比或线性化无关。由于功率转换器的存在，我们对实际上是直流和非线性的电网感兴趣。

1.1 直流电网中的潮流

直流微电网中的潮流与交流情况有一些相似之处，因此，我们在下面的文献综述中提到了交流潮流中的相关工作。然而，有一些重要的区别值得强调：首先，问题仍然存在于实数集中，允许使用实数而不是复数分析（例如，请注意，直流方程是解析的，而交流方程则不是）。其次，电网可以孤岛运行（即没有松弛节点），因此有必要在潮流问题中包含下垂控制。第三，直流电网具有与其对应的交流电网不存在的特性，例如， $Y_{B U S}$ 始终是对角线占优势的，而 $Z_{B U S }$ 是单调的（请注意，具有高电容效应的交流电网可能具有不存在的 $Y_{B U S}$ 对角占优）。因此，直流微电网中的潮流需要进行分析，而这些分析不能从交流情况中推断出来。

1.2 创新点和相关工作

在本文中，我们分析了牛顿法和近似牛顿法在直流微电网中潮流的收敛性。这种分析很重要，主要有两个原因：首先，潮流算法需要在微电网的运行和规划中多次执行。在操作中，在人工监督较少的智能电网环境中，保证收敛是一个理想的特征。在规划中，潮流可能是其他算法的一部分，特别是在启发式优化问题中。因此，解的二次收敛性和唯一性是关键条件。其次，潮流给出了电网动态模型的平衡点。在大多数与微电网的动力学和稳定性相关的研究中，找到平衡是第一步。

最近分析了高斯-赛德尔方法在主-从操作中的收敛性。在这里，我们通过定义牛顿方法在主从操作和岛式操作中的收敛的确切条件来证明这一结果。此外，我们还分析了一个近似的牛顿方法的收敛性。这个方法类似于交流电网的快速解耦负载流。我们对前者使用Kantorovitchs理论，对后者使用收缩映射理论。尽管这些理论是实际分析中的经典结果，但之前还没有人用这些理论来分析这些问题。正如预期的那样，牛顿方法具有二次收敛性，尽管是在一个小的吸引盆中，而近似的牛顿方法有一个保证的线性收敛性。

1.3 本文结构

本文的其余部分组织如下：第二节描述了主从和孤岛运行中的电网模型。第三节分析牛顿法，第四节分析近似牛顿法。之后，进行数值模拟，然后得出结论和参考。

2 数学/网络模型

2.1 主-从操作

见第5部分

2.2 孤岛运行

见第5部分

3 牛顿法

见第五部分

4 案例及Matlab代码实现

4.1 算例

在图 3 所示的直流微电网中进行了数值模拟，其参数在表 I 中给出。节点 1 是电压控制的，而节点 3、7、10 和 14 是步进节点（因此通过 Kron 减少消除）。实验表明，假设A2很容易在我们的测试系统中得到满足（即|Pm ax |< 1/ρ = 40.9 pu）。

图 3. 21 个节点的直流微电网图

表1 拟议的测试系统的参数

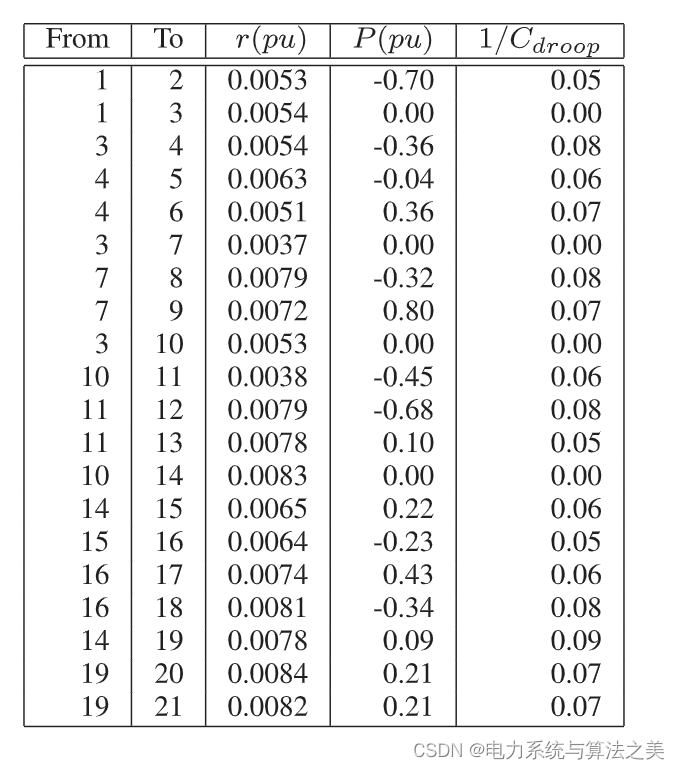
这是因为设计良好的直流微电网具有较小的电阻值以获得高效率。潮流是在四种情况下计算的：使用牛顿法和近似牛顿法，主从运行和孤岛运行（这意味着 3 中的开关打开）。

4.2 实现结果

4.3 分析

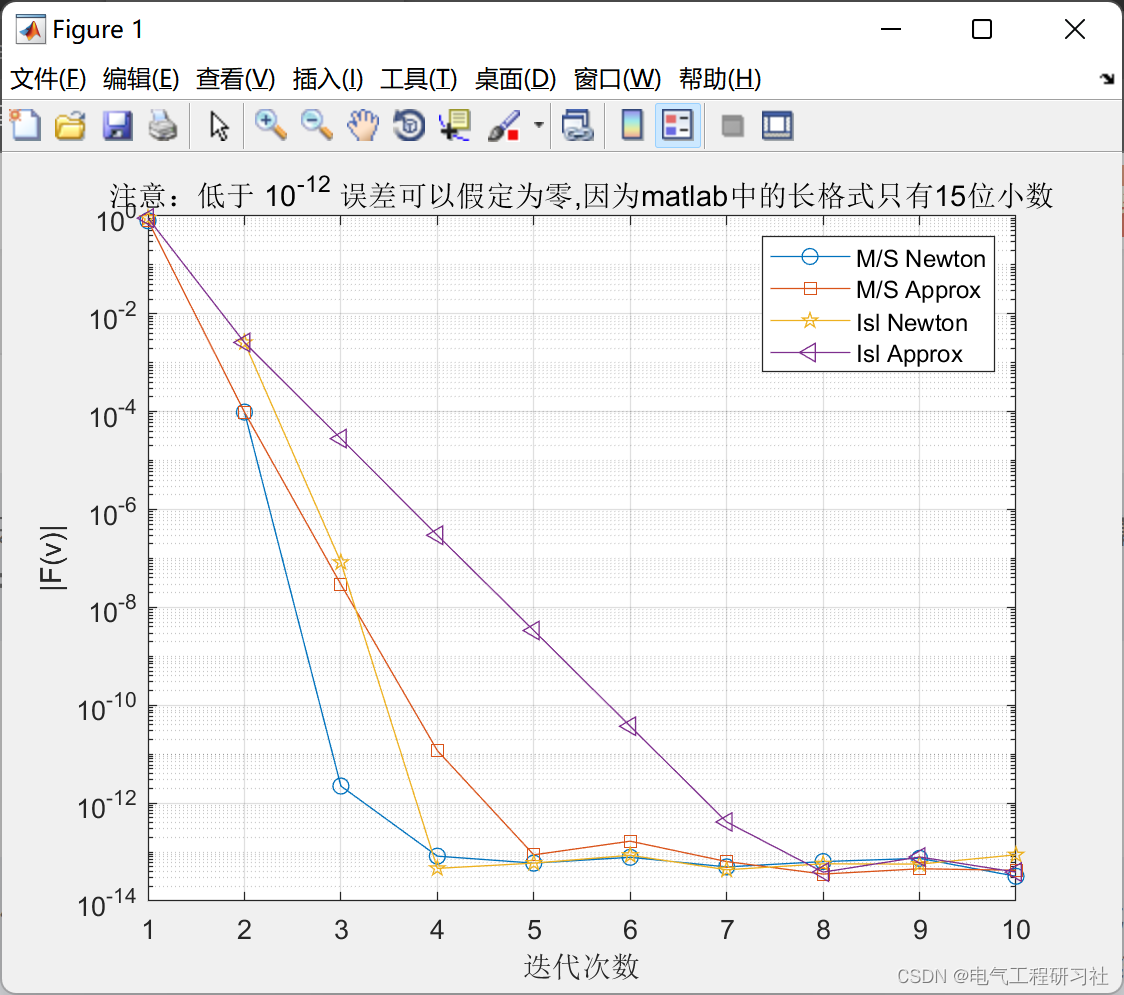
‖F (vk )‖的值在图 4 中给出了每次迭代。我们可以看到，牛顿法和近似牛顿法的第一次迭代是相同的。然而，随着算法的执行，牛顿法的误差如图 1 所示。表二主从操作收敛措施总结表三孤岛操作收敛措施总结在岛和主从操作中均以二次方减小，而近似牛顿法的误差线性减小。这种表现与命题 1 至 4 一致；事实上，这些通过数值模拟得出的结论，直接使用这些介词就可以得出。表 II 和 III 总结了这些结果。需要注意的是，本文提出的条件是充分但必要的。因此，我们的结果是保守但现实的收敛界限。这意味着，如果满足条件，我们可以保证该方法的收敛性。但是，如果某些条件不满足，并不意味着算法会发散。这是用于孤岛操作的近似牛顿方法的情况，在我们的示例中，它不满足命题 4 的条件（见表 III），但是，正如我们在图 4 中看到的那样，该算法实现了收敛。

图 4. 作为迭代函数的误差

表二主从操作收敛措施总结

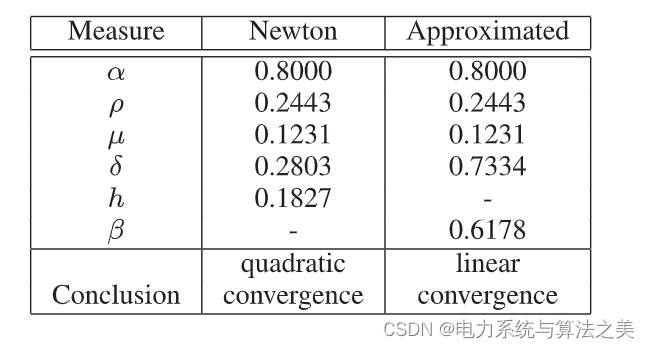
表三孤岛内操作的收敛措施摘要

部分代码：

error_4 = zeros(10,1);  % 仅10次迭代
DF = -diag((P+C.*v1)./(v.^2))-Ys;        
tic
for k = 1:10
    S = (P-C.*(v-v1))./v;
    F = S - Ys*v;
    DF = -diag(P+C.*v1)-Ys;
    v = v - DF\F;
    error_4(k) = norm(F,Inf);
end
t4 = toc;
v4 = v;
iter = 1:10;
figure(1);
semilogy(iter,error_1,'-o',iter,error_2,'-s',iter,error_3,'-p',iter,error_4,'-<')
grid on
ylabel('|F(v)|');
xlabel('迭代次数')
legend('M/S Newton','M/S Approx', 'Isl Newton', 'Isl Approx');
disp('每种情况下的电压值')
disp('M/S Newton    M/S Appx  Isd Newton  Isl Appx')
disp([v1 v2 v3 v4])
disp('每个案例的经过时间（以毫秒为单位）')
disp([t1 t2 t3 t4]*1E3)
title('注意：低于 10^{-12} 误差可以假定为零,因为matlab中的长格式只有15位小数')