1.设计思路
求解该题可以用分治法解题,总共有三种情况,最大子段在我们数组的左侧;最大子段在我们数组的右侧;最大子段跨过了左右两侧,在中间最大。第一种和第二种将两个子问题递归解出。分开的位置就是我们的中心位置。在第三种情况中假设跨过中心的子段在左侧的最大值为s1,在右侧的最大值为s2.则这个完整子段的最大值就是s1+s2,把问题分成了两个分别求解。
2.源代码
#define MAX 100
int maxsub(int left,int right);
int a[MAX];
int main()
{
int i,count;
scanf("%d",&count); //输入元素的个数
for(i=0;i<count;i++)
scanf("%d",&a[i]);
printf("%d\n",maxsub(0,count-1));
return 0;
}
int maxsub(int left,int right)
{
int center,i,sum,left_sum,right_sum,left_max,right_max;
center=(left+right)>>1;
if(left==right)
return a[left]>0?a[left]:0;
else
{
left_sum=maxsub(left,center);
right_sum=maxsub(center+1,right);
sum=0;
left_max=0;
for(i=center;i>=left;i--)
{
sum+=a[i];
if(sum>left_max)
left_max=sum;
}
sum=0;
right_max=0;
for(i=center+1;i<=right;i++)
{
sum+=a[i];
if(sum>right_max)
right_max=sum;
}
sum=right_max+left_max;
if(sum<left_sum)
sum=left_sum;
if(sum<right_sum)
sum=right_sum;
}
return sum;
}
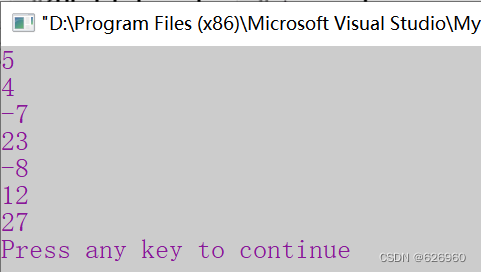
3.运行结果
5
4
-7
23
-8
12
27
(第一行为输入总元素的个数,第二至六行为输入的正整数和负整数,最后一行为最大子段和,即23-8+12=27。)








![[MySQL]MySQL索引](https://img-blog.csdnimg.cn/img_convert/482ab2582c789649db0e91cef9f5656c.png)