---

一、拓扑序列及其排序的相关概念

拓扑序列的定义

拓扑序列是对一个 有向无环图(DAG)（也称为拓扑图）而言的，有向图的拓扑序列是其顶点的线性排序，使得对每条有向边 (u,v)，u 在序列中出现在 v之前。

例如下图：

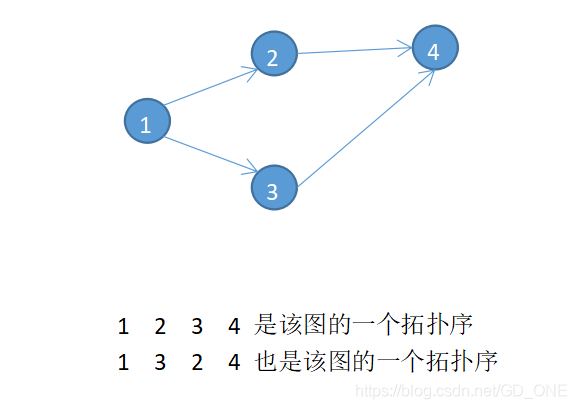
存在4条边：（1,3）（1,2）（2,4）（2,3）

该图的拓扑序列必须要满足以下两点：

• 每个顶点只出现一次。
• 对于图中的任何一条边，起点必须在终点之前。

拓扑序列的性质

• 对于一个有 n 个顶点的 DAG，可能存在多个不同的拓扑序列。
• 如果图中存在环，则不能得到拓扑序列。如果图中不存在环，则至少存在一个拓扑序列。
• 可以使用广度优先搜索、深度优先搜索等图遍历算法求解拓扑序列。
• 拓扑序列在很多场景下有应用，比如为工程项目排序建立先后关系、计算程序中任务的执行顺序等。
• 拓扑序列可以用于检测图中是否存在环。如果可以成功生成拓扑序列，说明图中没有环，反之则说明有环。
• 对于一个DAG，可以根据拓扑序列将其转化为等价的序列图。

出度、入度、度数

出度(Out-degree)：对于一个图中的某个顶点,出度表示从该顶点指向其他顶点的边的数量。它描述了从该顶点发散出去的连接数。

入度(In-degree)：对于一个图中的某个顶点,入度表示指向该顶点的边的数量。它描述了进入该顶点的连接数。

度数(Degree)：对于一个图中的某个顶点,度数等于其出度与入度的和。它描述了与该顶点相关的边的总数。

拓扑排序

①从图中选择一个入度为0的顶点，并输出该顶点；
②从图中删除该顶点及其相关联的有向边，调整被删除有向边的终点的入度（入度减1）；
③重复①和②；
④直到所有顶点均被输出，拓扑序列完成；否则，无拓扑序列。

如下图所示：

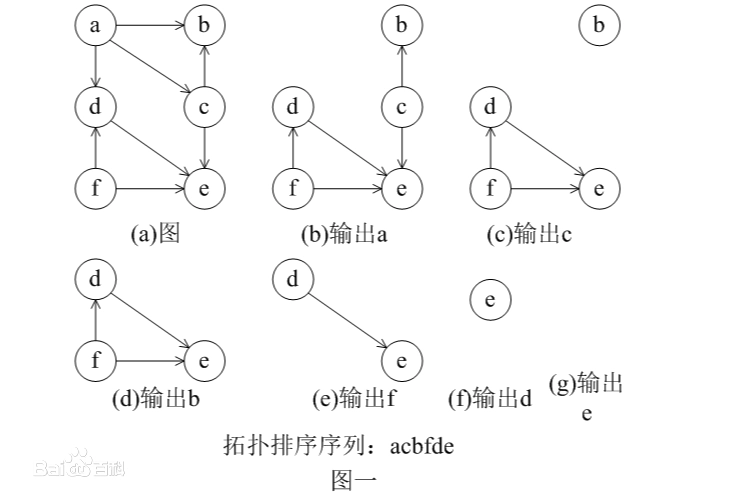
二、拓扑序列及其排序的应用

有向图的拓扑序列

题目描述：
给定一个 $n$ 个点 $m$ 条边的有向图，点的编号是 $1$ 到 $n$，图中可能存在重边和自环。

请输出任意一个该有向图的拓扑序列，如果拓扑序列不存在，则输出 −1。

若一个由图中所有点构成的序列 $A$ 满足：对于图中的每条边 $(x,y)$，$x$ 在 $A$ 中都出现在 $y$ 之前，则称 $A$ 是该图的一个拓扑序列。

输入格式：
第一行包含两个整数 $n$ 和 $m$。

接下来 m 行，每行包含两个整数 $x$ 和 $y$，表示存在一条从点 $x$ 到点 $y$ 的有向边 $(x,y)$。

输出格式：
共一行，如果存在拓扑序列，则输出任意一个合法的拓扑序列即可。否则输出−1。

数据范围：
$1\le n,m\le 10^5$

输入样例：

3 3
1 2
2 3
1 3

输出样例：

1 2 3

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<vector>
#include<queue>

using namespace std;

const int N = 1e5 + 10;
int h[N], e[N * 2], ne[N * 2], idx, n, m;
int d[N];
vector<int> path;

void add(int a, int b)
{
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}
bool topsort()
{
	queue<int> q;
	for (int i = 1; i <= n; ++i)
	{
		if (!d[i])
		{
			q.push(i);
			path.push_back(i);
		}
	}
	
	while (q.size())
	{
		auto t = q.front();
		q.pop();
		for (int i = h[t]; i != -1; i = ne[i])
		{
			int j = e[i];
			if (!(--d[j]))
			{
				path.push_back(j);
				q.push(j);
			}
		}
	}
	return path.size() == n;
}
int main()
{
	cin.tie(0);
	ios::sync_with_stdio(false);
	memset(h, -1, sizeof h);

	cin >> n >> m;
	for (int i = 1; i <= m; ++i)
	{
		int a, b;
		cin >> a >> b;
		add(a, b);
		d[b]++;
	}
	if (!topsort()) cout << "-1" << endl;
	else
	{
		for (auto u : path) cout << u << ' ';
		cout << endl;
	}
	return 0;
}