RNN基本介绍
概述
循环神经网络(Recurrent Neural Network,RNN)是一种深度学习模型,主要用于处理序列数据,如文本、语音、时间序列等具有时序关系的数据。
核心思想
RNN的关键思想是引入了循环结构,允许信息在网络内部进行传递。与传统的前馈神经网络(Feedforward Neural Network)不同,RNN在处理序列数据时会保留并利用先前的信息来影响后续的输出。
基本结构
RNN的基本结构是一个被称为“循环单元”(recurrent unit)的模块,它接收输入和先前的隐藏状态,并生成输出和新的隐藏状态。循环单元中的权重参数在时间步之间是共享的,这意味着它可以对序列中的不同位置应用相同的操作。
计算过程
RNN在每个时间步的计算过程如下:
1.接收当前时间步的输入和先前时间步的隐藏状态。
2.使用这些输入和隐藏状态计算当前时间步的输出。
3.更新隐藏状态,以便在下一个时间步使用。
优点
由于RNN具有循环结构,它可以在处理序列数据时保持记忆,并捕捉到序列中的长期依赖关系。这使得RNN在许多任务中表现出色,例如语言建模、机器翻译、语音识别、情感分析等。
缺点
然而,传统的RNN在处理长期依赖时存在梯度消失或梯度爆炸的问题,导致难以捕捉到远距离的依赖关系。
LSTM基本介绍
概述
LSTM(Long Short-Term Memory,长短期记忆网络)是一种循环神经网络(RNN)的改进型结构,用于解决传统RNN中的长期依赖问题。相比于传统的RNN,LSTM引入了门控机制,能够更好地捕捉和处理序列数据中的长期依赖关系。
核心思想
LSTM的核心思想是引入了三个门控单元:输入门(Input Gate)、遗忘门(Forget Gate)和输出门(Output Gate)。这些门控单元允许LSTM网络选择性地保留或丢弃信息,并且在传递信息时能够有效地控制梯度的流动。
基本结构
以下是LSTM中各个门控单元的功能:
1.输入门(Input Gate):决定当前时间步的输入信息中哪些部分需要被记忆。它使用sigmoid函数来产生一个0到1之间的值,描述了每个输入的重要性。
2.遗忘门(Forget Gate):决定之前的隐藏状态中哪些信息需要被遗忘。通过使用sigmoid函数,遗忘门可以控制先前的隐藏状态在当前时间步的重要性。
3.输出门(Output Gate):根据当前时间步的输入和之前的隐藏状态,决定应该输出多少信息到下一个时间步。输出门使用sigmoid函数来控制隐藏状态中的信息量,并使用tanh函数来生成当前时间步的输出。
优点
通过使用这些门控单元,LSTM网络能够在处理序列数据时灵活地控制信息的流动和记忆的保留。这使得LSTM能够更好地处理长期依赖关系,并在各种序列建模任务中表现出色,例如机器翻译、语音识别、文本生成等。
代码与详细注释
import torch
from torch import nn
import torchvision.datasets as dsets
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
# 可复现
# torch.manual_seed(1) # reproducible
# Hyper Parameters
EPOCH = 1 # train the training data n times, to save time, we just train 1 epoch
# 批大小
BATCH_SIZE = 64
TIME_STEP = 28 # rnn time step / image height
INPUT_SIZE = 28 # rnn input size / image width
LR = 0.01 # learning rate
DOWNLOAD_MNIST = True # set to True if haven't download the data
# Mnist digital dataset
train_data = dsets.MNIST(
root='./mnist/',
train=True, # this is training data
transform=transforms.ToTensor(), # Converts a PIL.Image or numpy.ndarray to
# torch.FloatTensor of shape (C x H x W) and normalize in the range [0.0, 1.0]
download=DOWNLOAD_MNIST, # download it if you don't have it
)
# plot one example
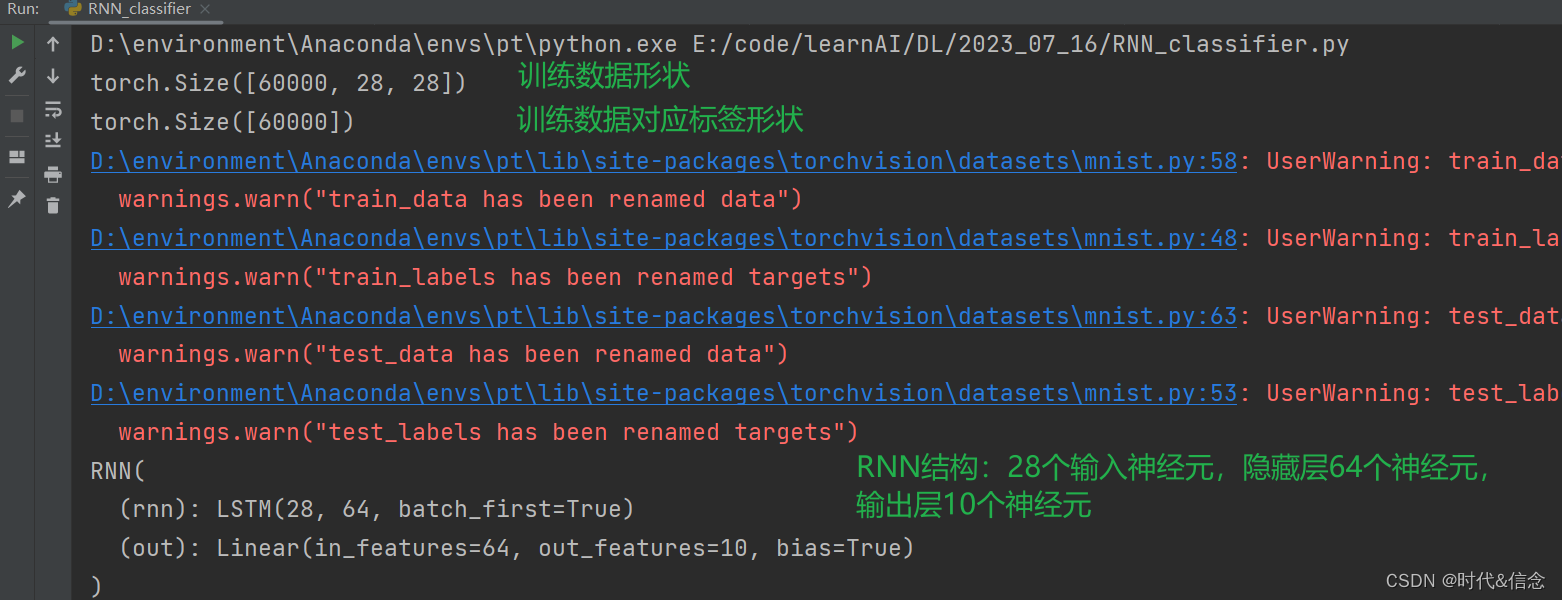
print(train_data.train_data.size()) # (60000, 28, 28)
print(train_data.train_labels.size()) # (60000)
plt.imshow(train_data.train_data[0].numpy(), cmap='gray')
plt.title('%i' % train_data.train_labels[0])
plt.show()
# Data Loader for easy mini-batch return in training
train_loader = torch.utils.data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)
# convert test data into Variable, pick 2000 samples to speed up testing
test_data = dsets.MNIST(root='./mnist/', train=False, transform=transforms.ToTensor())
test_x = test_data.test_data.type(torch.FloatTensor)[:2000]/255. # shape (2000, 28, 28) value in range(0,1)
test_y = test_data.test_labels.numpy()[:2000] # covert to numpy array
class RNN(nn.Module):
def __init__(self):
super(RNN, self).__init__()
self.rnn = nn.LSTM( # if use nn.RNN(), it hardly learns
input_size=INPUT_SIZE,
hidden_size=64, # rnn hidden unit
num_layers=1, # number of rnn layer
batch_first=True, # input & output will has batch size as 1s dimension. e.g. (batch, time_step, input_size)
)
self.out = nn.Linear(64, 10)
def forward(self, x):
# 输入向量的形状
# x shape (batch, time_step, input_size)
# r_out shape (batch, time_step, output_size)
# h_n shape (n_layers, batch, hidden_size)
# h_c shape (n_layers, batch, hidden_size)
r_out, (h_n, h_c) = self.rnn(x, None) # None represents zero initial hidden state
# choose r_out at the last time step
# 选择输出最后一步的r_out
out = self.out(r_out[:, -1, :])
return out
rnn = RNN()
print(rnn)
optimizer = torch.optim.Adam(rnn.parameters(), lr=LR) # optimize all cnn parameters
loss_func = nn.CrossEntropyLoss() # the target label is not one-hotted
# training and testing
for epoch in range(EPOCH):
for step, (b_x, b_y) in enumerate(train_loader): # gives batch data
b_x = b_x.view(-1, 28, 28) # reshape x to (batch, time_step, input_size)
output = rnn(b_x) # rnn output
loss = loss_func(output, b_y) # cross entropy loss
optimizer.zero_grad() # clear gradients for this training step
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
# 每训练50步之后,测试一下准确度
if step % 50 == 0:
test_output = rnn(test_x) # (samples, time_step, input_size)
pred_y = torch.max(test_output, 1)[1].data.numpy()
accuracy = float((pred_y == test_y).astype(int).sum()) / float(test_y.size)
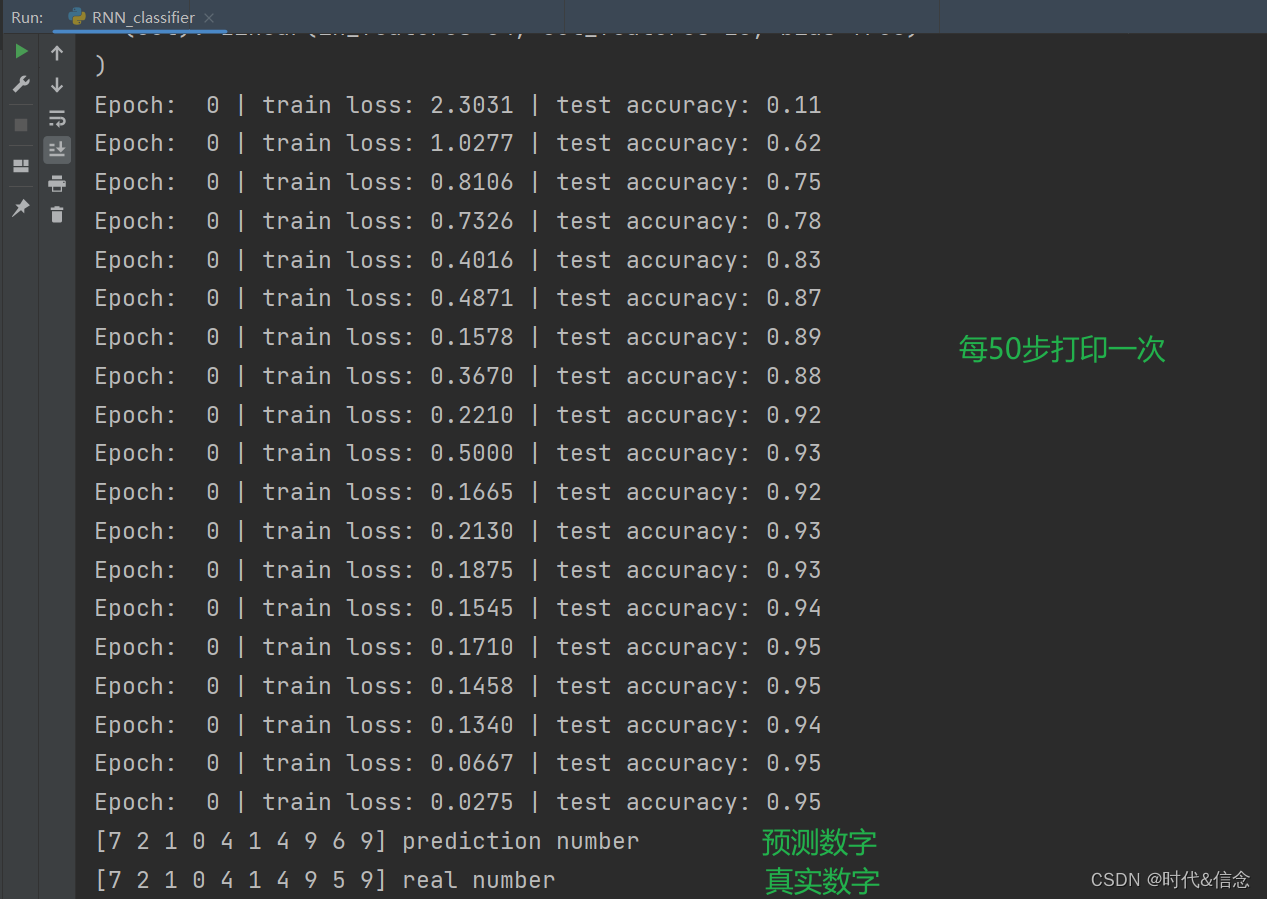
print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.numpy(), '| test accuracy: %.2f' % accuracy)
# print 10 predictions from test data
test_output = rnn(test_x[:10].view(-1, 28, 28))
pred_y = torch.max(test_output, 1)[1].data.numpy()
print(pred_y, 'prediction number')
print(test_y[:10], 'real number')
运行结果





![学习babylon.js --- [4] 体验WebVR](https://img-blog.csdnimg.cn/87983d87a5a64db4980a90b371001d40.png)