call zgeev('V', 'V', n, arr, lda, w, vl, ldvl, vr, ldvr, work, lwork, rwork, info)

这个函数是求矩阵的特征值，且结果是双精度复数的情况，具体可以查MKL的官方文档。

如果是单精度复数就要用cgeev，其中的参数也是将双精度改为单精度即可。

 其中的参数，

“V”，“V”：分别代表是否求矩阵的左特征向量还是右特征向量。选择“N”代表不求，其中有特征向量和Matlab的eig函数是一致的。

n:整数，数组arr的阶

arr：待求矩阵，如果结果是复数，就要把双精度的arr转换成复数形式。如：

                                                     arr_cmlx = cmplx(arr,0.0d0)

lda:整数，至少大于n

w:双精度复数，特征值，大小为(n)

vl：双精度复数，左特征向量，大小为(n,n)

ldvl：整数，至少大于n

vr：双精度复数，右特征向量，大小为(n,n)

ldvr：整数，至少大于n

work:整数，大小为2n

lwork: 整数，至少大于2n

rwork: 整数，至少大于2n。一般来说写2n没毛病，不过lwork，rwork具体的设置放上文档截图

info:整数，如果为0说明求解成功，如果为负数，比如-3代表第三个参数你设置的不对，-4代表第四个以此类推。如果是正数，如1，代表第一个特征值为0，解是奇异的，2代表第二个，以此类推。下面放一个例子，可以直接运行试试。

    program program
    use lapack95
    implicit none
    integer, parameter :: n = 3 ! 矩阵大小
    integer :: i, j, info, lda, ldvl, ldvr, lwork, rwork, work(2*n)
    complex*16 :: arr(n,n), w(n)
    complex*16 :: vl(n,n), vr(n,n)

    ! 初始化复数矩阵
    arr = reshape([(1.0, 2.0), (3.0, 4.0), (5.0, 6.0), &
        (7.0, 8.0), (9.0, 10.0), (11.0, 12.0), &
        (13.0, 14.0), (15.0, 16.0), (17.0, 18.0)], [n, n])

    lda = n
    ldvl = n
    ldvr = n
    lwork = 2*n
    rwork = 2*n
    ! 调用LAPACK库中的zgeev函数求解复数矩阵的特征值
    call zgeev('V', 'V', n, arr, lda, w, vl, ldvl, vr, ldvr, work, lwork, rwork, info)

    ! 打印特征值
    do i = 1, n
        print *, "Eigenvalue ", i, ": ", w(i)
    end do

    ! 打印特征向量
    do i = 1, n
        do j = 1, n
            write(*, '(F10.7,A,F10.7,A,2X)', advance='no') real(vr(i,j)), "+", aimag(vr(i,j)), "i"
        end do
        write(*,*) ! 换行
    end do
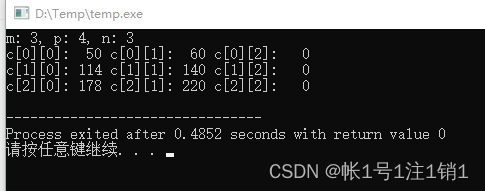
    end program

输出如下：
 Eigenvalue            1 :  (29.4359959090198,32.2251550243328)
 Eigenvalue            2 :  (-2.43599590901985,-2.22515502433279)
 Eigenvalue            3 :  (-4.037373503902555E-016,-5.245388153875226E-016)
 0.4594184+ 0.0083891i   0.8864625+ 0.0000000i  -0.4082483+ 0.0000000i
 0.5701955+ 0.0041945i   0.2481004+-0.0080782i   0.8164966+ 0.0000000i
 0.6809727+ 0.0000000i  -0.3902616+-0.0161565i  -0.4082483+ 0.0000000i
 

下面是相同matlab的结果:

 29.435995909019830 +32.225155024332800i
 -2.435995909019847 - 2.225155024332794i
 -0.000000000000000 - 0.000000000000001i

  0.459418381369183 + 0.008389093159843i  0.886462489565377 + 0.000000000000000i -0.408248290463862 + 0.000000000000000i
  0.570195542494289 + 0.004194546579922i  0.248100428415959 - 0.008078242749363i  0.816496580927726 + 0.000000000000000i
  0.680972703619395 + 0.000000000000000i -0.390261632733458 - 0.016156485498726i -0.408248290463863 + 0.000000000000000i

可以看到结果可以算是一致的。