🎇【数据结构】朴素模式匹配 & KMP 算法🎇

文章目录
- 🎇【数据结构】朴素模式匹配 & KMP 算法🎇
- 一.朴素模式匹配算法
- 1.用基本操作实现
- 2.不用基本操作实现
- 二. K M P KMP KMP算法
- 1.最长公共前后缀
- 2.理解 n e x t next next数组
- 3.求解 n e x t next next数组
- ①手算实现
- ②机算实现
- 4. k m p kmp kmp算法实现
- 三. K M P KMP KMP算法优化
一.朴素模式匹配算法
子串的定位操作通常称为串的模式匹配,它求的是模式串在主串中的位置,而朴素模式匹配就是一种不断移动主串指针,每一次都和模式串依次进行比较的暴力求解方法
思路:从主串的第一个位置起和模式串的第一个字符进行匹配,如果相等则继续匹配,否则从主串的第二个字符开始逐一比较,以此类推,直到全部匹配完成

我们来看朴素模式算法的时间复杂度:
最坏的情况是:当模式串为"0000001",而主串为"000000000000000000001"时,由于模式串的前6个字符均为0,主串的前20个字符也为0,因此,每趟匹配都要匹配到最后一个元素才会匹配失败,而要回溯15次,总比较次数为: 15 × 7 = 105 15×7=105 15×7=105次

因此,我们可以总结出朴素模式算法的缺点为:当某些子串与模式串能部分匹配时,指针i的经常回溯,导致时间开销大
1.用基本操作实现
其实,再之前串的基本操作中,我们就介绍了串的定位操作,这也是串的匹配实现
//1.求子串
bool SubString(SString& Sub, SString S, int pos, int len) { //Sub为子串,S为主串
if (pos + len - 1 > S.len) //如果求的子串长度比总长度要大,则返回
return false;
for (int i = pos; i <= pos + len - 1; i++) {
Sub.ch[i - pos + 1] = S.ch[i]; //第一个元素不存
}
Sub.len = len;
return true;
}
//2.比较串
int StrCompare(SString S, SString T) {
for (int i = 1; i <= S.len && i <= T.len; i++) { //同时在两个串长以内
if (S.ch[i] != T.ch[i])
return S.ch[i] - T.ch[i]; //返回该元素的ASCII差值
}
return S.len - T.len; //如果扫描过的字符全部相同,则长的更大
}
//3.定位
int Index(SString S, SString T) { //定位子串T在主串S中的位置
int i = 1, n = S.len, m = T.len;
SString sub; //记录子串
while (i <= n - m + 1) {
SubString(sub, S, i, m); //求子串
if (StrCompare(sub, T) != 0) //每一次都比较子串和T,如果子串不等于T,继续遍历下一个子串
++i;
else
return i;
}
return 0;
}
2.不用基本操作实现
🔱思路分析:
- 我们将定义两个指针 i , j i,j i,j,一个指向主串,一个指向子串
- 当
i
,
j
i,j
i,j都不超过各自串的长度时:
① 如果此时 i , j i,j i,j位置指向的值相等,则继续比较下一个元素, i , j i,j i,j均向后移一位;
② 如果此时 i , j i,j i,j位置指向的值不相等,则让主串指针 i i i回溯,指向之前指向的首位置的下一个, j j j指针指向子串的第一个; - 重复操作,直到结束
🎯 注意点:
-
i = i − j + 2 i=i-j+2 i=i−j+2
我们可以用图来直观地理解
也就是说,可以将 i − j = 2 i-j=2 i−j=2变为 i − ( j − 1 ) + 1 i-(j-1)+1 i−(j−1)+1
其中 i − ( j − 1 ) i-(j-1) i−(j−1)表示 i i i 之前指向的首个位置, + 1 +1 +1则表示, i i i 向后移动一步
-
i − T . l e n i-T.len i−T.len
因为若最后一个元素匹配成功,则 i , j i,j i,j 指针均会加 1,而此时 i i i 指向下一个位置, j j j 指向 T . l e n + 1 T.len+1 T.len+1位置
于是,若 j > T . l e n j>T.len j>T.len,则表明模式串所有字符都匹配成功,则此时 i i i 减去模式串长度即为子串在主串中的首位置; 反之,则表明没有匹配成功
功能函数实现:
int Index(SString S, SString T) {
int i = 1, j = 1; //指向两个串的指针
while (i <= S.len && j <= T.len) {
if (S.ch[i] == T.ch[j]) {
++i;
++j;
}
else {
i = i - j + 2; //向后移一位
j = 1;
}
}
if (j > T.len)
return i - T.len;
else
return 0;
}
完整代码实现:
#include<iostream>
#define Maxsize 50
using namespace std;
typedef struct {
char ch[Maxsize];
int len;
}SString,*String;
void InitString(SString& S) {
S.len = 0;
}
void StrAssign(SString& S, char chars[]) {
int i = 0;
while (chars[i] != '\0') {
S.ch[i + 1] = chars[i];
S.len++;
i++;
}
}
int Index(SString S, SString T) {
int i = 1, j = 1; //指向两个串的指针
while (i <= S.len && j <= T.len) {
if (S.ch[i] == T.ch[j]) {
++i;
++j;
}
else {
i = i - j + 2; //向后移一位
j = 1;
}
}
if (j > T.len)
return i - T.len;
else
return 0;
}
int main() {
SString S, T;
InitString(S);
InitString(T);
char s[] = "xiaoyanbaobaodan";
char t[] = "yanbaobao";
StrAssign(S, s);
StrAssign(T, t);
cout << "模式串T在S中的位置为:" << Index(S,T) << endl;
system("pause");
return 0;
}
输出结果:

二. K M P KMP KMP算法
实际上,KMP算法就是消除指针i的回溯,让i指针只进不退,而只移动模式串指针指向位置的方法
怎么理解呢?我们进一步来看

1.最长公共前后缀
在了解KMP算法之前,我们先要了解一个概念,就是最长公共前后缀
基本概念:
前缀:指除了最后一个字符以外,字符串的全部头部子串
后缀:指除了第一个字符以外,字符串的全部尾部子串
最长公共前后缀:即当前字符串构成的前缀集合和后缀集合,取交集,相同且相等的字符串,即为最长公共前后缀
✅ e . g : e.g: e.g:
以"ababa"为例:
- 'a’的前后缀均为 ∅,最长的相等前后缀长度为0;
- 'ab’的前缀为{a},后缀为{b},则交集为 ∅,最长公共前后缀长度为0;
- 'aba’的前后缀为{a,ab},后缀为{a,ba},交集为 {a},最长公共前后缀长度为1;
- 'abab’的前缀为{a,ab,aba},后缀为{b,ab,bab},交集为 {ab},最长公共前后缀长度为2;
- 'ababa’的前缀为{a,ab,aba,abab},后缀为{a,ba,aba,baba},交集为{a,aba},最长公共前后缀长度为3;
因此,我们得到了字符串"ababa"的最长公共前后缀长度为 0 0 1 2 3
我们现在来思考,我们得到这个值有什么用呢?
回到字符串匹配问题,对于模式串"ababc"和主串"ababababc"来说,有PM[]数组:


此时,当第5个位置不匹配时,我们需要移动指向模式串的指针 j j j,若我们指向第4个位置(也就是模式串向后移动一个位置),但是,蓝色划线部分的前面是不匹配的,因此,我们还需要往后移动一个,才可以让蓝色划线之前的字符串匹配成功(“ab”)
我们的思考就在,能不能预测到这一次的匹配失败呢?
答案当然是可以的!
用公共前后缀判断:因为此时123位置的元素为"aba",而234位置的元素为"bab",所以,肯定是不能成功匹配的,因为它不是前四个字符串"abab"的公共前后缀
对于"abab",我们对其进行内部匹配:发现它无法匹配,也就预测了次移动方法一定不行!!!


✅ 核心思想:
当前指向的是第5个位置,要想移动后保证尽可能多的前面的字符匹配,又因为前4个字符与主串已经匹配成功,我们就需要得到前4个元素的最大公共前后缀,只需要将该最大公共前缀串移动至后缀串位置(此时两个子串相同),就能保证移动后匹配的字符长度最大

这是书上的图,可以方便比较一下:
所以我们只需要找到此时的最长公共前后缀即可

2.理解 n e x t next next数组
我们在上面得到了最长公共前后缀数组,记为 P M [ ] PM[] PM[],并可以得到 移动步数的规律:
M o v e = 已匹配的字符串长度 − 最长公共前后缀长度 Move=已匹配的字符串长度-最长公共前后缀长度 Move=已匹配的字符串长度−最长公共前后缀长度
那么,我们接下来要进一步研究这一结论
因为已匹配的字符串长度为 j − 1 j-1 j−1,而前 j − 1 j-1 j−1个字符的最长公共前后缀长度为 P M [ j − 1 ] PM[j-1] PM[j−1]
所以写成:
M o v e = j − 1 − P M [ j − 1 ] Move=j-1-PM[j-1] Move=j−1−PM[j−1]
我们不妨将 P M PM PM数组统一向后移动一位,这样 j − 1 j-1 j−1变为 j j j,就表示当j位置的字符不匹配时,应该移动的步数为:
M o v e = j − 1 − P M [ j ] Move=j-1-PM[j] Move=j−1−PM[j]

🎯 注意:
- 原来PM数组的第一个元素右移之后变为-1,因为若第一个字符不匹配,则一定需要将模式串向右移动一位,所以不用计算;
- 原来PM数组的最后一个元素溢出而删除,因为原来最后一个元素PM[j]是在指针指向 j + 1 j+1 j+1时才会使用的,而字符串总长就只有 j j j,因此,删去将不会影响结果
这样,当第 j 个字符不匹配时,只用看自己底下的PM数组值就好啦~

为了便于计算,再改进,将PM数组的值统一 +1,与 j-1中的 -1抵消,于是,我们得到了next数组:
M o v e = j − n e x t [ j ] Move=j-next[j] Move=j−next[j]

因为当模式串指针j不匹配时,指针j会移动到:
j = j − M o v e j=j-Move j=j−Move 位置处
所以,代入Move值,最终得到了子串指针移动位置公式:
j = n e x t [ j ] j=next[j] j=next[j]
✅ 我们最后来看一看next数组的含义:
n e x t [ j ] next[j] next[j]的含义是:在子串的第 j j j 个位置与主串发生匹配失败时,则指针跳到子串的 n e x t [ j ] next[j] next[j]位置处,重新与当前位置的主串字符比较
🎯 总结:
到这里,说了这么多,其实就是两个东西
- 🍰子串滑动距离:
M o v e = 已匹配字符串长度 − 已匹配子串的最大公共前后缀长度 Move=已匹配字符串长度-已匹配子串的最大公共前后缀长度 Move=已匹配字符串长度−已匹配子串的最大公共前后缀长度 - 🍰
n
e
x
t
[
j
]
next[j]
next[j]:当
j
j
j 不匹配时,
j
j
j 要移动至子串的位置为:
j ′ = 已匹配子串的最大公共前后缀长度 + 1 j'=已匹配子串的最大公共前后缀长度 +1 j′=已匹配子串的最大公共前后缀长度+1
3.求解 n e x t next next数组
当然,还没结束,接下来,我们还要推导 next数组的一般公式:

①手算实现
step:
在不匹配处划一条分界线,模式串一步步向后退,直到分界线前面的字符串与主串相匹配,则让指向模式串的指针j指向分界线右侧的第一个字符
图解算法:

此时,主串指针 i = 5 i=5 i=5,则 n e x t [ 5 ] = 3 next[5]=3 next[5]=3
②机算实现
✅科学算法:设主串为" s 1 s 2... s n s1s2...sn s1s2...sn",模式串为" p 1 p 2... p m p1p2...pm p1p2...pm",当主串中第 i i i 个元素与模式串中第 j j j 个元素不匹配时,最长公共前后缀串应该移动至多远,然后与模式串中哪个字符匹配呢?
假设此时应该与模式中第k个字符进行比较,则模式中前
k
−
1
k-1
k−1个字符的子串应该满足下列条件:
"
p
1
p
2...
p
k
−
1
"
=
"
p
j
−
k
+
1
p
j
−
k
+
2
.
.
.
p
j
−
1
"
"p1p2...p_{k-1}"="p_{j-k+1}p_{j-k+2}...p_{j-1}"
"p1p2...pk−1"="pj−k+1pj−k+2...pj−1"
若存在满足上述条件的子串,则发生失配时,只需将模式串滑至 p k pk pk字符和主串中 s i si si字符对齐即可
图解:

可以看出,当不存在上述的子序列时,即 k = 1 k=1 k=1,显然应该将模式串移动 j − 1 j-1 j−1 个位置,将模式串第一个字符与主串第 i i i 个字符比较,因此,当 j = 1 j=1 j=1时, n e x t [ 1 ] = 0 next[1]=0 next[1]=0
我们先引出next数组求解公式:

✅ 公式解释:
- 当
j
=
1
j=1
j=1 时,为什么要取
n
e
x
t
[
j
]
=
0
next[j]=0
next[j]=0?
当第一个字符与主串不匹配时,可以理解为主串的第 i i i 个位置与模式串的第 0 0 0个位置对齐,所以应该同时将指针 i i i 和 j j j 向右移动一个位置
- 为什么要取
m
a
x
(
k
)
max(k)
max(k),
k
k
k最大是多少?
当主串的第 i i i 个字符与模式串的第 j j j 个字符配对失败时,因为 k k k为模式串的下一次比较位置, k k k 值可能有多个,但为了不使向右移动丢失可能得匹配,所以要使右移的距离应该尽可能小,即右移距离 M o v e = j − n e x t [ j ] Move=j-next[j] Move=j−next[j]应该尽可能小,应该取max{k}
- 其他情况是什么,为什么要取
n
e
x
t
[
j
]
=
1
next[j]=1
next[j]=1?
除了上面两种情况,发生失配时,主串指针 i i i 不回溯,在最坏的情况下,模式串从第1个位置与主串 i i i 位置进行比较
掌握了next的一般公式,接下来我们来看代码如何实现:
首先我们肯定知道: n e x t [ 1 ] = 0 next[1]=0 next[1]=0 是确定的
我们的思考是:假设我们已知了 n e x t [ j ] = k next[j]=k next[j]=k,那么怎么递推得到 n e x t [ j + 1 ] next[j+1] next[j+1]呢?
这里设此时的 k k k满足上述条件: " p 1 p 2 . . . p k − 1 " = " p j − k + 1 p j − k + 2 . . . p j − 1 " "p_1p_2...p_{k-1}"="p_{j-k+1}p_{j-k+2}...p_{j-1}" "p1p2...pk−1"="pj−k+1pj−k+2...pj−1",也就是当第 j − 1 j-1 j−1个位置失配时,移动至第 k k k个位置
于是,有两种情况:
-
p k = p j p_k=p_j pk=pj:
则在模式串中表现为: " p 1 p 2... p k " = " p j − k + 1 . . . p j " "p1p2...p_k"="p_{j-k+1}...pj" "p1p2...pk"="pj−k+1...pj"

所以此时,若 i i i与 j + 1 j+1 j+1位置失配,应该移动至 k + 1 k+1 k+1位置比较:
n e x t [ j + 1 ] = n e x t [ j ] + 1 next[j+1]=next[j]+1 next[j+1]=next[j]+1
if (T.ch[k]==T.ch[j]){
++k;++j;
next[j]=k;
}
-
p k ≠ p j p_k≠p_j pk=pj:

我们可以把 n e x t next next函数值的求解问题转化为模式匹配问题:
也就是将当前的前缀" p 1 . . . p k p_1...p_k p1...pk"与后缀" p j − k + 1 . . . p j p_{j-k+1}...p_{j} pj−k+1...pj"进行模式匹配,这样找到前 j j j 个元素的更小的相等的前后缀
由于此时" p 1 . . . p k − 1 p_1...p_{k-1} p1...pk−1"和" p j − k + 1 . . p j p_{j-k+1}..p_j pj−k+1..pj"都是相同的,所以这时候相当于将 j 1 j1 j1指针指向前缀, j 1 j1 j1不断前移, j 2 j2 j2指针指向后缀, j 2 j2 j2不断后移(这里 j 1 j1 j1 是主动指针,而 j 2 j2 j2 相当于从动指针),因为只要保证他们一直为之前的公共前缀,就可以不用在意这 k ′ − 1 k'-1 k′−1长度的子串,这样主要考虑的就是要找到前缀中的一个值 p k ′ = p j p_k'=p_j pk′=pj
所以,要保证长度为k’-1的前后缀相同:
k ′ = n e x t [ k ] k'=next[k] k′=next[k],若与 p j p_j pj不相同,继续取 k ′ = n e x t [ n e x t [ k ] ] k'=next[next[k]] k′=next[next[k]]
✅ ①若能找到相等的 p k ′ p_{k'} pk′为止,满足:
" p 1 p 2... p k ′ " = " p j − k ′ + 1 . . . p j " "p1p2...p_{k'}"="p_{j-k'+1}...pj" "p1p2...pk′"="pj−k′+1...pj"
n e x t [ j + 1 ] = k ′ + 1 next[j+1]=k'+1 next[j+1]=k′+1
✅ ②若不能找到相等的 p k ′ p_{k'} pk′,则下一次从第一个位置开始比较,即:
n e x t [ j + 1 ] = 1 next[j+1]=1 next[j+1]=1
e . g e.g e.g:上述情况就是均不能匹配时, n e x t [ 7 ] = 1 next[7]=1 next[7]=1

如果不理解可以看看手算草稿:
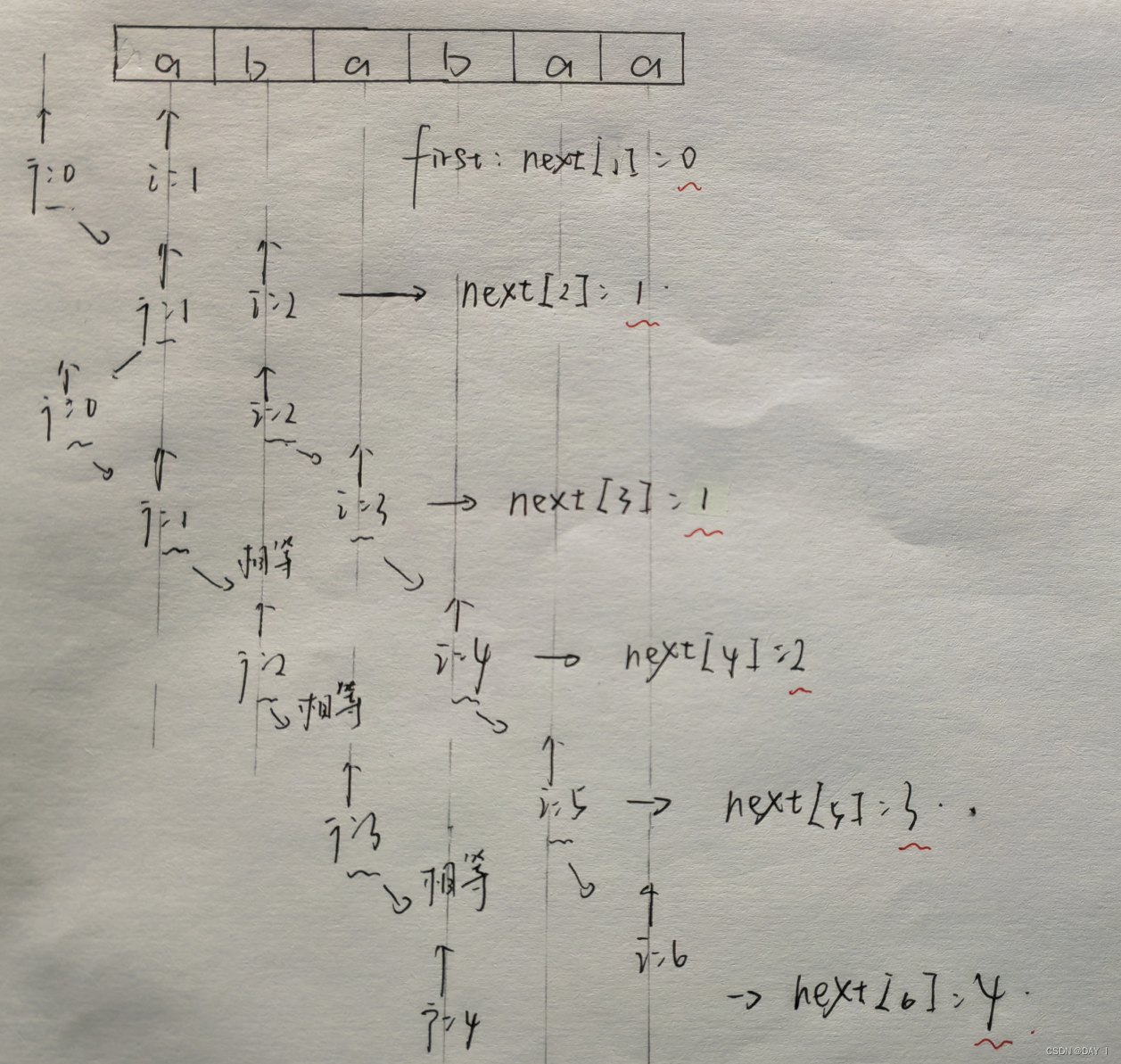

则当 j为前缀指针,i为后缀指针时,有如下代码:
//求next数组
void Get_next(SString& S,int next[]) {
int i = 1, j = 0;
next[1] = 0;
while (i < S.len) {
if (j == 0 || S.ch[i] == S.ch[j]) { //也就是 pk==pj 时
++i; ++j;
next[i] = j; //这里保证i>1时,next[i]>=1
}
else {
j = next[j]; //j移动至当前公共前后缀的下一位置
}
}
}
至此,就是求解next数组的全部内容啦~!
4. k m p kmp kmp算法实现
🎯其实,在得到了next数组后,kmp的匹配算法相对要简单地多,它在形式上与朴素模式算法很相似,不同之处仅在于当匹配模式过程中产生失配时,指针i不变,指针j退回到next[j]的位置(最长公共前后缀的前缀串的下一个位置)并重新比较,并且当指针j=0时,指针i与指针j同时加1,即若主串的第i个位置与模式串的第一个位置不匹配,应该从主串的i+1位置匹配

K
M
P
KMP
KMP 算法的 时间复杂度:
O
(
m
+
n
)
O(m+n)
O(m+n)

k m p kmp kmp代码实现:
//kmp模式匹配
int Kmp(SString S, SString T,int next[]) {
int i = 1, j = 1;
while (i <= S.len && j <= T.len) {
if (j == 0 || S.ch[i] == T.ch[j]) {
i++; j++; //如果匹配,就继续比较后面一个元素
}
else {
j = next[j]; //如果不匹配,j移动下一个位置
}
}
if (j > T.len)
return i - T.len;
else
return 0;
}
完整 k m p kmp kmp算法实现:
#include<iostream>
#define Maxsize 50
using namespace std;
typedef struct {
char ch[Maxsize];
int len;
}SString, * String;
void InitString(SString& S) {
S.len = 0;
}
void StrAssign(SString& S, char chars[]) {
int i = 0;
while (chars[i] != '\0') {
S.ch[i + 1] = chars[i];
S.len++;
i++;
}
}
//求next数组
void Get_next(SString& S,int next[]) {
int i = 1, j = 0;
next[1] = 0;
while (i < S.len) {
if (j == 0 || S.ch[i] == S.ch[j]) { //也就是 pk==pj 时
++i; ++j;
next[i] = j; //这里保证i>1时,next[i]>=1
}
else {
j = next[j]; //j移动至当前公共前后缀的下一位置
}
}
}
//kmp模式匹配
int Kmp(SString S, SString T,int next[]) {
int i = 1, j = 1;
while (i <= S.len && j <= T.len) {
if (j == 0 || S.ch[i] == T.ch[j]) {
i++; j++; //如果匹配,就继续比较后面一个元素
}
else {
j = next[j]; //如果不匹配,j移动下一个位置
}
}
if (j > T.len)
return i - T.len;
else
return 0;
}
int main() {
SString S, T;
InitString(S);
InitString(T);
char s[] = "ababacababcda";
char t[] = "ababc";
StrAssign(S, s);
StrAssign(T, t);
//构造next数组
int next[Maxsize];
Get_next(S, next);
//kmp模式匹配
int index = Kmp(S, T, next);
cout <<"kmp算法下,得到模式串T在主串中的位置是:" << index << endl;
system("pause");
return 0;
}
输出结果:
三. K M P KMP KMP算法优化
你以为就结束了?你以为
k
m
p
kmp
kmp算法已经是最好了?没错,它甚至还可以优化!

🎁 比如,当模式串"aaaab"和主串"aaacaaaab"进行匹配时:

当i=4,j=4时, s 4 s_4 s4跟 p 4 p_4 p4失配,如果用之前的next数组还需要进行 s 4 s_4 s4与 p 3 p_3 p3、 p 2 p_2 p2、 p 1 p_1 p1进行3次匹配,事实上,因为 p n e x t [ 4 ] = 3 = p 4 = a p_{next[4]=3}=p_4=a pnext[4]=3=p4=a、 p n e x t [ 3 ] = 2 = p 3 = a p_{next[3]=2}=p_3=a pnext[3]=2=p3=a, p n e x t [ 2 ] = 1 = p 2 = a p_{next[2]=1}=p_2=a pnext[2]=1=p2=a,显然后面三次匹配都是无意义的,那么问题出在哪呢?
问题在于,不应该出现 p j = p n e x t [ j ] p_j=p_{next[j]} pj=pnext[j]
理由是:当 p j ≠ s j p_j≠s_j pj=sj时,下一次必然是 p n e x t [ j ] 与 s j p_{next[j]}与s_j pnext[j]与sj进行比较,但是如果 p j = p n e x t [ j ] p_j=p_{next[j]} pj=pnext[j]时,就会出现上述情况,发现不相等后,又再次取 n e x t [ n e x t [ j ] ] next[next[j]] next[next[j]],这样必然导致继续失配,就会不断进行重复的比较
那么遇到这种情况应该如何处理呢?
✅ 其实,我们只需要改变next数组,将这里的 n e x t [ j ] 修改为 n e x t [ n e x t [ j ] ] next[j]修改为next[next[j]] next[j]修改为next[next[j]],不断从前往后递归,并改名为nextval数组,则可得到最终结果
如果不理解可以再看看手算的草稿:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sDBeIGpa-1689495018149)(2023-04-25-21-33-20.png)]](https://img-blog.csdnimg.cn/2b201d1b344540ce80f367b26b617491.png)

求解nextval数组:
只需要多一层判断即可
//求nextval数组
void Get_nextval(SString& S, int nextval[]) {
int i = 1, j = 0;
nextval[1] = 0;
while (i < S.len) {
if (j == 0 || S.ch[i] == S.ch[j]) {
++i; ++j;
if (S.ch[i] != S.ch[j]) //增加条件
nextval[i] = j;
else
nextval[i] = nextval[j]; //也就是相等的情况下,等于next[j]
}
else {
j = nextval[j]; //j移动至当前公共前后缀的下一位置
}
}
}
完整代码实现:
#include<iostream>
#define Maxsize 50
using namespace std;
typedef struct {
char ch[Maxsize];
int len;
}SString, * String;
void InitString(SString& S) {
S.len = 0;
}
void StrAssign(SString& S, char chars[]) {
int i = 0;
while (chars[i] != '\0') {
S.ch[i + 1] = chars[i];
S.len++;
i++;
}
}
//求nextval数组
void Get_nextval(SString& S, int nextval[]) {
int i = 1, j = 0;
nextval[1] = 0;
while (i < S.len) {
if (j == 0 || S.ch[i] == S.ch[j]) {
++i; ++j;
if (S.ch[i] != S.ch[j]) //增加条件
nextval[i] = j;
else
nextval[i] = nextval[j]; //也就是相等的情况下,等于next[j]
}
else {
j = nextval[j]; //j移动至当前公共前后缀的下一位置
}
}
}
//kmp匹配
int Kmp(SString S, SString T, int nextval[]) {
int i = 1, j = 1;
while (i <= S.len && j <= T.len) {
if (j == 0 || S.ch[i] == T.ch[j]) {
i++; j++; //如果匹配,就继续比较后面一个元素
}
else {
j = nextval[j]; //如果不匹配,j移动下一个位置
}
}
if (j > T.len)
return i - T.len;
else
return 0;
}
int main() {
SString S, T;
InitString(S);
InitString(T);
char s[] = "ababacababcda";
char t[] = "ababc";
StrAssign(S, s);
StrAssign(T, t);
//构造nextval数组
int nextval[Maxsize];
Get_nextval(S, nextval);
//kmp模式匹配
int index = Kmp(S, T, nextval);
cout << "kmp优化后,得到模式串T在主串中的位置是:" << index << endl;
system("pause");
return 0;
}
输出结果: