文章和代码已经归档至【Github仓库：https://github.com/timerring/dive-into-AI 】或者公众号【AIShareLab】回复 pytorch教程 也可获取。

文章目录

Pytorch：权值初始化
- 梯度消失与梯度爆炸
Xavier 方法与 Kaiming 方法
- Xavier 方法
- nn.init.calculate_gain()
- Kaiming 方法
常用初始化方法

Pytorch：权值初始化

在搭建好网络模型之后，首先需要对网络模型中的权值进行初始化。权值初始化的作用有很多，通常，一个好的权值初始化将会加快模型的收敛，而比较差的权值初始化将会引发梯度爆炸或者梯度消失。下面将具体解释其中的原因：

梯度消失与梯度爆炸

考虑一个 3 层的全连接网络。

$H_{1}=X \times W_{1}$ ， $H_{2}=H_{1} \times W_{2}$ ， $Out=H_{2} \times W_{3}$ ，如下图所示，

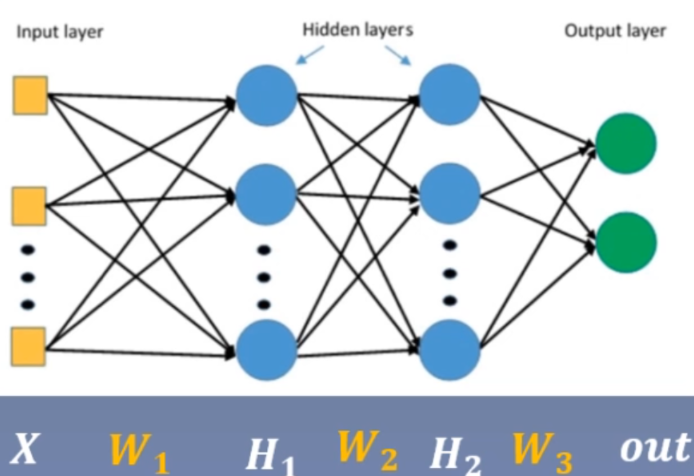
其中第 2 层的权重梯度如下：

$\begin{array}{l} \mathrm{H}_{2}=\mathrm{H}_{1} * \mathrm{~W}_{\mathbf{2}} \\ \Delta \mathrm{W}_{\mathbf{2}}=\frac{\partial \text { Loss }}{\partial \mathrm{W}_{2}}=\frac{\partial \mathrm{Loss}}{\partial \text { out }} * \frac{\partial \text { out }}{\partial \mathrm{H}_{2}} * \frac{\partial \mathrm{H}_{2}}{\partial \mathrm{W}_{2}} \\ =\frac{\partial \text { Loss }}{\partial \text { out }} * \frac{\partial \text { out }}{\partial \mathrm{H}_{2}} * \mathrm{H}_{1} \\ \end{array}$

由上式化简可知，如果H_1发生以下变化，那么对应的梯度也就会发生变化：

梯度消失: $\mathrm{H}_{1} \rightarrow 0 \Rightarrow \Delta \mathrm{W}_{2} \rightarrow 0$
梯度爆炸: $\mathrm{H}{1} \rightarrow \infty \Rightarrow \Delta \mathrm{W}{2} \rightarrow \infty $

因此，为了避免以上两种情况，就必须严格控制网络层输出的数值范围。

具体可以通过构建 100 层全连接网络，先不使用非线性激活函数，每层的权重初始化为服从 $N (0, 1)$ 的正态分布，输出数据使用随机初始化的数据，这样的例子来直观地感受影响：

import torch
import torch.nn as nn
from common_tools import set_seed

set_seed(1)  # 设置随机种子

class MLP(nn.Module):
    def __init__(self, neural_num, layers):
        super(MLP, self).__init__()
        self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
        self.neural_num = neural_num

    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)
        return x

    def initialize(self):
        for m in self.modules():
            # 判断这一层是否为线性层，如果为线性层则初始化权值
            if isinstance(m, nn.Linear):
                nn.init.normal_(m.weight.data)    # normal: mean=0, std=1
# 网络的层数
layer_nums = 100
# 神经元的个数
neural_nums = 256
batch_size = 16

net = MLP(neural_nums, layer_nums)
net.initialize()
# 设置随机初始化的输入
inputs = torch.randn((batch_size, neural_nums))  # normal: mean=0, std=1

output = net(inputs)
print(output)

输出为：

tensor([[nan, nan, nan,  ..., nan, nan, nan],
        [nan, nan, nan,  ..., nan, nan, nan],
        [nan, nan, nan,  ..., nan, nan, nan],
        ...,
        [nan, nan, nan,  ..., nan, nan, nan],
        [nan, nan, nan,  ..., nan, nan, nan],
        [nan, nan, nan,  ..., nan, nan, nan]], grad_fn=<MmBackward>)

通过输出可知，输出值均为nan，即非数字类型，原因可能是数据太大(梯度爆炸)或者太小(梯度消失)。

为了具体知道是在哪一层开始出现nan的，我们可以在forward函数中添加判断得知，查看每一次前向转播的标准差是否是nan，若是，则停止前向传播并输出。

这里判断是否为nan时采用了 torch.isnan 函数

    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)

            print("layer:{}, std:{}".format(i, x.std()))
            if torch.isnan(x.std()):
                print("output is nan in {} layers".format(i))
                break

        return x

输出如下：

layer:0, std:15.959932327270508
layer:1, std:256.6237487792969
layer:2, std:4107.24560546875
.
.
.
layer:29, std:1.322983152787379e+36
layer:30, std:2.0786820453988485e+37
layer:31, std:nan
output is nan in 31 layers

可见，之际上输出的标准差是逐层递增的，具体为什么会导致这种情况：

$\times Y)=E(X) \times E(Y)$ ：两个相互独立的随机变量的乘积的期望等于它们的期望的乘积。
$D(X)=E(X^{2}) - [E(X)]^{2}$ ：一个随机变量的方差等于它的平方的期望减去期望的平方
$D (X + Y) = D (X) + D (Y)$ ：两个相互独立的随机变量之和的方差等于它们的方差的和。

可以推导出两个随机变量的乘积的方差如下：

$\times Y)=E[(XY)^{2}] - [E(XY)]^{2}=D(X) \times D(Y) + D(X) \times [E(Y)]^{2} + D(Y) \times [E(X)]^{2}$

又由于输入变量是符合标准的正态分布的，因此 $E (X) = 0$ ， $E (Y) = 0$ ，可知 $\times Y)=D(X) \times D(Y)$

我们以输入层第一个神经元为例：

$\mathrm{H}_{11}=\sum_{i=0}^{n} X_{i} * W_{1 i}$

其中输入 X 和权值 W 都是服从 $N (0, 1)$ 的正态分布，且由公式 $\times Y)=D(X) \times D(Y)$ , 因此这个神经元的方差为：

$\begin{aligned} \mathbf{D}\left(\mathrm{H}_{11}\right) &=\sum_{i=0}^{n} D\left(X_{i}\right) * D\left(W_{1 i}\right) \\ &=n *(1 * 1) \\ &=n \end{aligned}$

可以求其标准差： $\operatorname{std}\left(\mathrm{H}_{11}\right)=\sqrt{\mathrm{D}\left(\mathrm{H}_{11}\right)}=\sqrt{n}$

可见，经过第一层网络，方差就会扩大 n 倍，标准差就扩大 $\sqrt{n}$ 倍，n 为每层神经元个数，直到超出数值表示范围。

从前面的输出中也可以看出来，n = 256，因此每一层的标准差输出都是16倍。再由公式可知，每一层网络输出的方差与神经元个数、输入数据的方差、权值方差有关（见上式），通过观察可知，比较好改变的是权值的方差 $D (W)$ ，要控制每一层输出的方差仍然为1左右，因此需要 $\frac{1}{n}$ ，可知标准差为 $std(W)=\sqrt\frac{1}{n}$ 。因此修改权值初始化代码为nn.init.normal_(m.weight.data, std=np.sqrt(1/self.neural_num))

再次输出时，结果如下：

layer:0, std:0.9974957704544067
layer:1, std:1.0024365186691284
layer:2, std:1.002745509147644
.
.
.
layer:94, std:1.031973123550415
layer:95, std:1.0413124561309814
layer:96, std:1.0817031860351562

修改之后，没有出现梯度消失或者梯度爆炸的情况，每层神经元输出的方差均在 1 左右。通过恰当的权值初始化，可以保持权值在更新过程中维持在一定范围之内。

但是上述的实验前提为未使用非线性函数的前提下，如果在forward()中添加非线性变换例如tanh，每一层的输出方差会越来越小，会导致梯度消失。

为了解决这个问题，进一步有了著名的 Xavier 初始化与 Kaiming 初始化。

Xavier 方法与 Kaiming 方法

Xavier 方法

Xavier 是 2010 年提出的，针对有非线性激活函数时的权值初始化方法。

目标是保持数据的方差维持在 1 左右
针对饱和激活函数如 sigmoid 和 tanh 等。

同时考虑前向传播和反向传播，需要满足两个等式

$\begin{array}{l} \boldsymbol{n}_{\boldsymbol{i}} * \boldsymbol{D}(\boldsymbol{W})=\mathbf{1} \\ \boldsymbol{n}_{\boldsymbol{i}+\mathbf{1}} * \boldsymbol{D}(\boldsymbol{W})=\mathbf{1} \\ \end{array}$

通过计算可知： $D(W)=\frac{2}{n_{i}+n_{i+1}}$ 。

为了使 Xavier 方法初始化的权值服从均匀分布，假设 $W$ 服从均匀分布 $U [- a, a]$ ，那么方差 $D(W)=\frac{(-a-a)^{2}}{12}=\frac{(2 a){2}}{12}=\frac{a{2}}{3}$ ，令 $\frac{2}{n_{i}+n_{i+1}}=\frac{a^{2}}{3}$ ，解得： $\boldsymbol{a}=\frac{\sqrt{6}}{\sqrt{n_{i}+n_{i+1}}}$ ，所以 $W$ 服从分布 $U\left[-\frac{\sqrt{6}}{\sqrt{n_{i}+n_{i+1}}}, \frac{\sqrt{6}}{\sqrt{n_{i}+n_{i+1}}}\right]$

所以初始化方法改为：

a = np.sqrt(6 / (self.neural_num + self.neural_num))
# 把 a 变换到 tanh，计算增益
tanh_gain = nn.init.calculate_gain('tanh')
a *= tanh_gain

nn.init.uniform_(m.weight.data, -a, a)

并且每一层的激活函数都使用 tanh，输出如下：

layer:0, std:0.7571136355400085
layer:1, std:0.6924336552619934
layer:2, std:0.6677976846694946
.
.
.
layer:97, std:0.6426210403442383
layer:98, std:0.6407480835914612
layer:99, std:0.6442216038703918

可以看到每层输出的方差都维持在 0.6 左右。

也可以直接调用PyTorch 中 Xavier 初始化方法：

tanh_gain = nn.init.calculate_gain('tanh')
nn.init.xavier_uniform_(m.weight.data, gain=tanh_gain)

nn.init.calculate_gain()

这里重点介绍一下nn.init.calculate_gain(nonlinearity,param=**None**)方法。

主要功能是经过一个分布的方差经过激活函数后的变化尺度，主要有两个参数：

nonlinearity：激活函数名称
param：激活函数的参数，如 Leaky ReLU 的 negative_slop等等。

下面是计算标准差经过激活函数的变化尺度的代码。

x = torch.randn(10000)
out = torch.tanh(x)
# 计算变化尺度（也可以称为变化倍数）
gain = x.std() / out.std()
print('gain:{}'.format(gain))

tanh_gain = nn.init.calculate_gain('tanh')
print('tanh_gain in PyTorch:', tanh_gain)

输出如下：

gain:1.5982500314712524
tanh_gain in PyTorch: 1.6666666666666667

结果表示，原有数据分布的方差经过 tanh 之后，标准差会变小 1.6 倍左右。

Kaiming 方法

虽然 Xavier 方法提出了针对饱和激活函数的权值初始化方法，但是 AlexNet 出现后，大量网络开始使用非饱和的激活函数如 ReLU 等，这时 Xavier 方法不再适用。2015 年针对 ReLU 及其变种等激活函数提出了 Kaiming 初始化方法。

针对 ReLU，方差应该满足： $\mathrm{D}(W)=\frac{2}{n_{i}}$ ；

针对 ReLu 的变种，方差应该满足： $D(W)=\frac{2}{\left(1+\mathrm{a}^{2}\right) * n_{i}}$ ，a 表示负半轴的斜率，如 PReLU 方法，标准差满足 $\operatorname{std}(W)=\sqrt{\frac{2}{\left(1+a^{2}\right) * n_{i}}}$ 。