一、说明
统计学是数学的一个分支,涉及数据的收集、解释、组织和解释。本博客旨在回答以下问题:
1. 什么是描述性统计?2. 描述性统计的类型?3. 集中趋势的度量(平均值、中位数、模式)
4. 散布/离差度量(标准差、平均偏差、方差、百分位数、四分位数、四分位数间距)5. 什么是偏度?6. 什么是峰度?7. 什么是相关性?今天,让我们一劳永逸地理解描述性统计数据。让我们开始吧!
二、什么是描述性统计?
描述性统计涉及汇总和组织数据,以便于理解。与推论统计不同,描述性统计试图描述数据,但不试图从样本到整个总体进行推断。在这里,我们通常描述样本中的数据。这通常意味着描述性统计与推论统计不同,不是在概率论的基础上发展起来的。
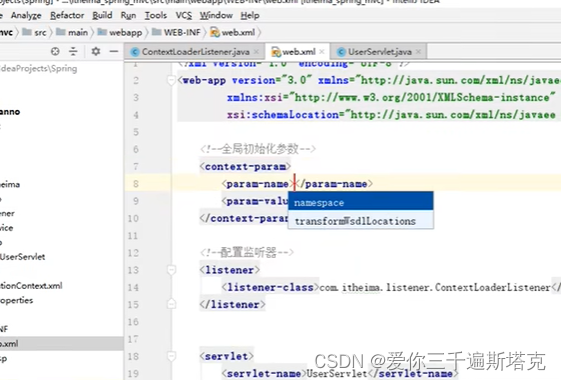
2.1 描述性统计的类型?
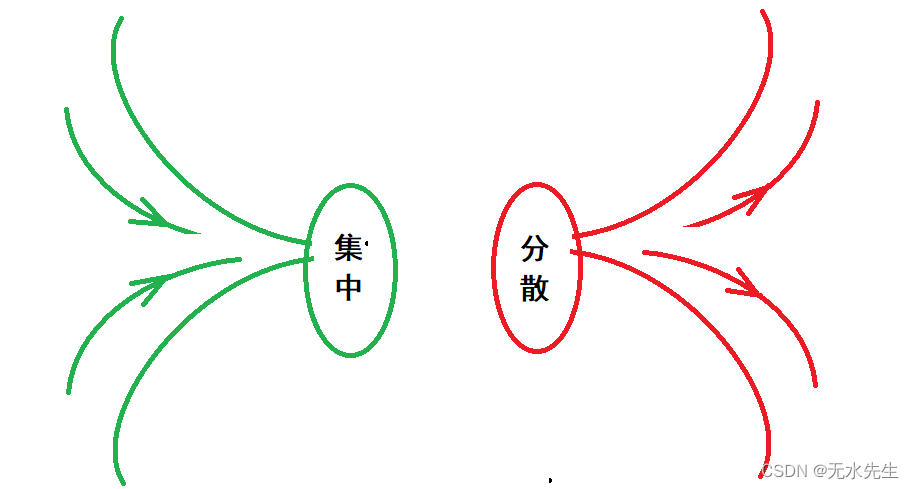
描述性统计分为两类。集中趋势的度量和变异性(传播)的度量。注意,这其实是非常单纯的方法。
2.2 集中趋势的度量
集中趋势是指有一个数字最能概括整组测量值的想法,这个数字在某种程度上是该集合的“中心”。
2.2.1 平均值/平均值
平均值或平均值是数据的集中趋势,即整个数据围绕其展开的数字。在某种程度上,它是一个可以估计整个数据集值的数字。
让我们计算具有 8 个整数的数据集的平均值。
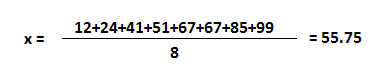
2.2.2 中位数
中位数是将数据分成 2 个相等部分的值,即当数据按升序或降序排列时,右侧的项数与左侧的项数相同。
注意:如果按降序对数据进行排序,则不会影响中位数,但 IQR 将为负数。我们将在本博客的后面讨论 IQR。
如果项数为奇数,则中位数将是中间项.如果多个项是偶数,则中位数将是中间 2 项的平均值。
![]()
中位数为 59,它将一组数字分成相等的两部分。由于集合中有偶数,答案是中间数字 51 和 67 的平均值。
注意: 当值处于算术级数时(连续项之间的差异是恒定的。这里是 2.),中位数总是等于平均值。
![]()
这 5 个数字的平均值是 6,因此是中位数。
2.2.3 频率模式
模式是在数据集中出现的最长时间的项,即具有最高频率的项。
![]()
在此数据集中,模式为 67,因为它具有比其他值多的值,即两次。
但是可能存在一个数据集,其中根本没有模式,因为所有值出现的次数相同。如果两个值同时出现并且比其他值多,则数据集是双峰的。如果三个值同时出现并且比其他值多,则数据集是三峰的,对于 n 个模式,该数据集是多模态的。
2.3 扩散/分散的测量
点差度量是指数据中可变性的概念。
2.3.1 标准差
标准差是每个数量和平均值之间平均距离的度量。也就是说,数据如何从平均值中分布。低标准差表示数据点往往接近数据集的平均值,而高标准差表示数据点分布在更广泛的值范围内。
在某些情况下,我们必须在样本或总体标准差之间进行选择。
当我们被要求找到人口中某一部分的SD时,一部分人口;然后我们使用样本标准差。
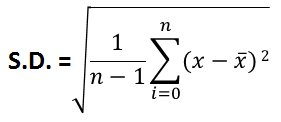
其中 x̅ 是样本的平均值。
但是当我们必须处理整个总体时,我们使用总体标准差。
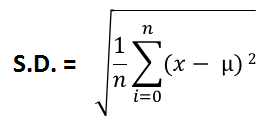
其中μ是人口的平均数。
虽然样本是总体的一部分,但它们的SD公式应该是相同的,但事实并非如此。要了解更多信息,请参阅此链接
如您所知,在描述性统计中,我们通常处理样本中可用的数据,而不是总体中的数据。因此,如果我们使用前面的数据集,并替换示例公式中的值,
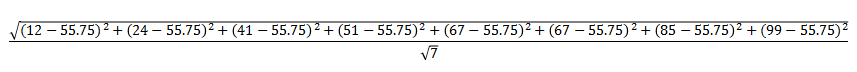
答案是29.62。
2.3.2 平均偏差/平均绝对偏差
它是一组值中每个值之间的绝对差值的平均值,以及该集合中所有值的平均值。
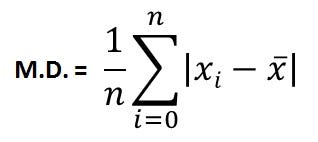
因此,如果我们使用以前的数据集,并替换值,
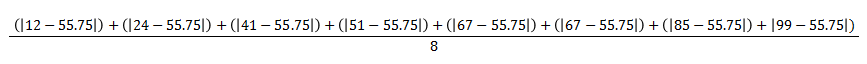
答案是23.75。
2.3.3 方差
方差是每个数量和平均值之间平均距离的平方。也就是说,它是标准差的平方。
![]()
答案是877.34。
2.3.4 范围
范围是最简单的描述性统计技术之一。它是最低值和最高值之间的差异。
![]()
范围为 99–12 = 87
2.3.5 百分比
百分位数是一种表示值在数据集中的位置的方法。要计算百分位数,数据集中的值应始终按升序排列。
![]()
中位数 59 在 4 个值中比自身少 8 个。也可以说是:在数据集中,59 是第 50 个百分位数,因为总项的 50% 小于 59。通常,如果 k 是第 n 个百分位数,则意味着总项的 n% 小于 k。
2.3.6 四分位数
在统计和概率中,四分位数是将数据划分为多个季度的值,前提是数据按升序排序。
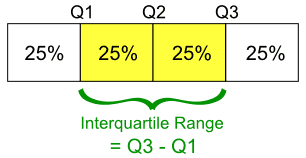
四分位数 [图片 14] (图片提供:IQR | Intro to Statistical Methods)
有三个四分位数值。第一个四分位数值为 25%。第二个四分位数是 50 百分位数,第三个四分位数是 75 百分位数。第二个四分位数(Q2)是整个数据的中位数。第一个四分位数 (Q1) 是数据上半部分的中位数。第三四分位数(Q3)是数据下半部分的中位数。
![]()
所以在这里,通过类比,
Q2 = 67:是整个数据的 50 个百分位数,为中位数。
Q1 = 41:是数据的 25 个百分位数。
Q3 = 85:是日期的 75 个百分位数。
四分位距 (IQR) = Q3 - Q1 = 85 - 41 = 44
注意: 如果按降序对数据进行排序,IQR 将为 -44。幅度将是相同的,只是符号会有所不同。如果数据按降序排列,则负 IQR 很好。只是我们从较大的值中否定较小的值,我们更喜欢升序(Q3 - Q1)。
三、偏度
3.1 偏度定义
偏度是实值随机变量关于其平均值的概率分布不对称性的度量。偏度值可以是正值、负值或未定义值。
在完美正态分布中,曲线两侧的尾部是彼此的精确镜像。
当分布向左偏斜时,曲线左侧的尾部比右侧的尾部长,并且均值小于众数。这种情况也称为负偏度。
当分布向右倾斜时,曲线右侧的尾部比左侧的尾部长,并且均值大于众数。这种情况也称为正偏度。
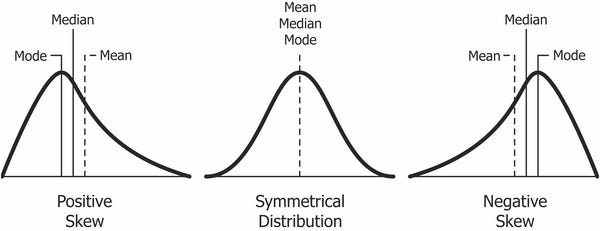
偏度 [图片 16] (图片提供:Skewness - Clojure for Data Science [Book])
3.2 如何计算偏度系数?
要计算样本的偏度系数,有两种方法:
1] 皮尔逊偏度第一系数(模偏度)

2] 皮尔逊第二偏度系数(中值偏度)

解释
- 偏度的方向由标志给出。零意味着完全没有偏度。
- 负值表示分布呈负偏斜。正值表示分布呈正偏态。
- 该系数将样本分布与正态分布进行比较。值越大,分布与正态分布的差异越大。
示例问题:使用 Pearson 系数 #1 和 #2 查找具有以下特征的数据的偏度:
- 平均值 = 50。
- 中位数 = 56。
- 模式 = 60。
- 标准差 = 8.5。
皮尔逊第一偏度系数:-1.17。
皮尔逊第二偏度系数:-2.117。
注意:皮尔逊的第一个偏度系数使用该模式。因此,如果值的频率非常低,那么它将无法给出集中趋势的稳定度量。例如,这两组数据中的模式均为 9:
1, 2, 3, 4, 4, 5, 6, 7, 8, 9.
在第一组数据中,该模式仅出现两次。因此,使用皮尔逊第一偏度系数不是一个好主意。但在第二盘,
1, 2, 3, 4, 4, 4, 4, 4, 4, 4, 4, 5, 6, 7, 8, 9, 10, 12, 12, 13.
模式 4 出现 8 次。因此,皮尔逊的第二偏度系数可能会给你一个合理的结果。
四、峰度
4.1 峰度定义
对峰度测量的确切解释曾经存在争议,但现在已解决。这是关于异常值的存在。峰度是衡量数据相对于正态分布是重尾(大量异常值)还是轻尾(缺乏异常值)的度量。

峰度 [图片 19] (图片提供:MVP Programs Help — MVP Programs Help Files)
4.2 峰度有三种类型
4.2.1 中生
峰度与正态分布峰度相似,为零。
4.2.2 钩端库尔特
分布是峰度大于中生分布的分布。这种分布的尾巴又厚又重。如果分布曲线比中生曲线更尖峰,则称为钩端曲线。
4.2.3 鸭嘴兽
分布是峰度小于中生分布的分布。这种分布的尾巴变薄。如果分布曲线的峰值小于中库尔特曲线,则称为鸭嘴曲线。
偏度和峰度之间的主要区别在于,偏度是指对称程度,而峰度是指分布中异常值的存在程度。
五、相关
相关性是一种统计技术,可以显示变量对是否相关以及相关性有多强。
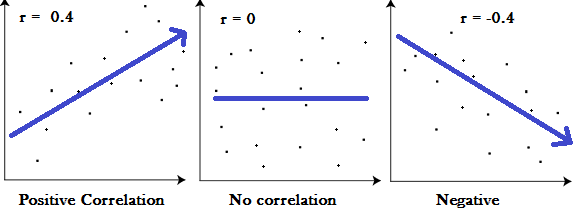
Correlation in Statistics: Correlation Analysis Explained - Statistics How To)
相关性的主要结果称为相关系数(或“r”)。它的范围从 -1.0 到 +1.0。r 越接近 +1 或 -1,两个变量的相关性就越密切。
如果 r 接近 0,则表示变量之间没有关系。如果 r 为正,则意味着当一个变量变大时,另一个变量变大。如果r为负,则意味着随着一个变大,另一个变小(通常称为“负”相关性)。
我希望我已经让你对描述性统计的确切含义有所了解。这是一些基本统计技术的基本概述,可以帮助您长期理解数据科学。