PCA

PCA 是一种流行的统计技术，用于识别数据集中最重要的特征或模式并将其转换为较低维的表示形式。本报告将涵盖PCA的基本原理、其优点。

步骤

主成分分析是一种数学技术，可降低数据集的维数，同时保留尽可能多的信息。它通过查找主成分来实现这一点，主成分是表示数据中最大方差方向的正交向量。

• 数据标准化：PCA 通常从数据标准化开始，以确保所有变量具有相似的尺度。此步骤涉及减去每个变量的平均值并除以其标准差
• 协方差矩阵计算：下一步是计算标准化数据的协方差矩阵。协方差矩阵提供有关数据集中变量对之间的关​​系和方差的信息。
  协方差矩阵衡量数据集中变量对之间的关​​系和方差。计算公式：
  $Cov(\mathbf{X})=\frac{1}{n}\cdot (\mathbf{X}-\mu )\cdot {(\mathbf{X}-\mu )}^{\mathsf{T}}$。这里$Cov(\mathbf{X})$是协方差矩阵，$\mu$是平均向量，$n$是$\mathbf{X}的行数$。
  协方差矩阵求出来是$m\ast m$的矩阵$m$是特征数量。对角线的值是方差（自身的协方差），非对角线上的是协方差，用协方差来表示两个特征之间相关性。协方差大于0，意味着两个特征正相关，小于0负相关，等于0无关。
• 特征分解：然后对协方差矩阵进行特征分解，产生矩阵的特征值和特征向量。特征向量表示主成分，相应的特征值表示每个成分解释的方差量。
  求协方差矩阵的特征值和特征向量: { ( λ 1 , μ 1 ) , ( λ 2 , μ 2 ) ⋯ ( λ m , μ m ) } \{{(\lambda _{1},\mu _1),(\lambda _{2},\mu _2)}\cdots(\lambda _{m},\mu _m)\} {(λ1​,μ1​),(λ2​,μ2​)⋯(λm​,μm​)}
• 成分选择和投影：主成分根据其相应的特征值进行排序，最高特征值表示解释数据中最大方差的成分。选择所需数量的主成分，并将数据投影到这些成分上以获得较低维的表示。
  我们认为特征值越大，代表越多的信息，所以取几个比较大的特征值抛弃剩下的就是降维后的$\mathbf{X}$

import numpy as np
from sklearn.decomposition import PCA

# Create a sample dataset
X = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])

# Initialize PCA with the desired number of components
n_components = 2
pca = PCA(n_components=n_components)

# Fit the data to PCA
pca.fit(X)

# Access the principal components
principal_components = pca.components_

# Transform the data to the lower-dimensional representation
X_transformed = pca.transform(X)

# Access the explained variance ratio
explained_variance_ratio = pca.explained_variance_ratio_

# Print the results
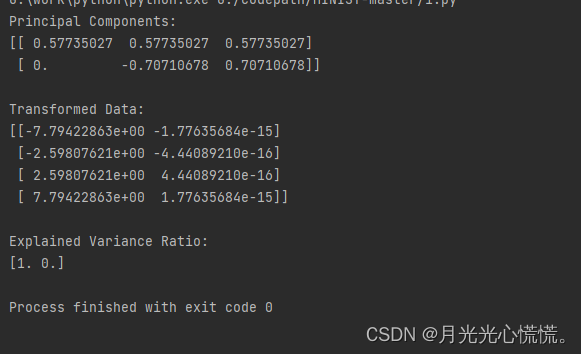
print("Principal Components:")
print(principal_components)
print("\nTransformed Data:")
print(X_transformed)
print("\nExplained Variance Ratio:")
print(explained_variance_ratio)

sklearn库里面有PCA的包，使用的时候可以直接调用，n_components是需要保留的主成分数量，使用方法 fit() 将数据拟合X到 PCA ，使用components属性访问主成分，使用方法 transform() 访问转换后的数据。

CNN基本代码

继上周学习CNN后，这周开始体验一下CNN的一些Demo。找数据集真的难受，找不到合适的，最后还是用教学数据集MNIST吧。这个数据集的好处就是是gz文件，不用进行数据预处理，很规范。

import torch
import torch.nn as nn
import torch.utils.data as Data
import torchvision
import cv2

导包

torch.manual_seed(1)  # 使用随机化种子使神经网络的初始化每次都相同

# 超参数
EPOCH = 1  # 训练整批数据的次数
BATCH_SIZE = 50
LR = 0.001  # 学习率
DOWNLOAD_MNIST = True  # 表示还没有下载数据集，如果数据集下载好了就写False

# 下载mnist手写数据集
train_data = torchvision.datasets.MNIST(
    root='./data/',  # 保存或提取的位置  会放在当前文件夹中
    train=True,  # true说明是用于训练的数据，false说明是用于测试的数据
    transform=torchvision.transforms.ToTensor(),  # 转换PIL.Image or numpy.ndarray

    download=DOWNLOAD_MNIST,  # 已经下载了就不需要下载了
)

test_data = torchvision.datasets.MNIST(
    root='./data/',
    train=False  # 表明是测试集
)

# 批训练 50个samples， 1  channel，28x28 (50,1,28,28)
# Torch中的DataLoader是用来包装数据的工具，它能帮我们有效迭代数据，这样就可以进行批训练
train_loader = Data.DataLoader(
    dataset=train_data,
    batch_size=BATCH_SIZE,
    shuffle=True  # 是否打乱数据，一般都打乱
)

# 进行测试
# 为节约时间，测试时只测试前2000个
#
test_x = torch.unsqueeze(test_data.train_data, dim=1).type(torch.FloatTensor)[:2000] / 255
# torch.unsqueeze(a) 是用来对数据维度进行扩充，这样shape就从(2000,28,28)->(2000,1,28,28)
# 图像的pixel本来是0到255之间，除以255对图像进行归一化使取值范围在(0,1)
test_y = test_data.test_labels[:2000]

class CNN(nn.Module):  # 我们建立的CNN继承nn.Module这个模块
    def __init__(self):
        super(CNN, self).__init__()
        self.conv1 = nn.Sequential(
            # 第一个卷积con2d
            nn.Conv2d(  # 输入图像大小(1,28,28)
                in_channels=1,  # 输入图片的高度，因为minist数据集是灰度图像只有一个通道
                out_channels=16,  # n_filters 卷积核的高度
                kernel_size=5,  # filter size 卷积核的大小 也就是长x宽=5x5
                stride=1,  # 步长
                padding=2,  # 想要con2d输出的图片长宽不变，就进行补零操作 padding = (kernel_size-1)/2
            ),  # 输出图像大小(16,28,28)
            # 激活函数
            nn.ReLU(),
            # 池化，下采样
            nn.MaxPool2d(kernel_size=2),  # 在2x2空间下采样
            # 输出图像大小(16,14,14)
        )
        # 建立第二个卷积(Conv2d)-> 激励函数(ReLU)->池化(MaxPooling)
        self.conv2 = nn.Sequential(
            # 输入图像大小(16,14,14)
            nn.Conv2d(  # 也可以直接简化写成nn.Conv2d(16,32,5,1,2)
                in_channels=16,
                out_channels=32,
                kernel_size=5,
                stride=1,
                padding=2
            ),
            # 输出图像大小 (32,14,14)
            nn.ReLU(),
            nn.MaxPool2d(2),
            # 输出图像大小(32,7,7)
        )
        # 建立全卷积连接层
        self.out = nn.Linear(32 * 7 * 7, 10)  # 输出是10个类

    # 下面定义x的传播路线
    def forward(self, x):
        x = self.conv1(x)  # x先通过conv1
        x = self.conv2(x)  # 再通过conv2
        # 把每一个批次的每一个输入都拉成一个维度，即(batch_size,32*7*7)
        # 因为pytorch里特征的形式是[bs,channel,h,w]，所以x.size(0)就是batchsize
        x = x.view(x.size(0), -1)  # view就是把x弄成batchsize行个tensor
        output = self.out(x)
        return output


cnn = CNN()
print(cnn)

optimizer = torch.optim.Adam(cnn.parameters(), lr=LR)
# 损失函数
loss_func = nn.CrossEntropyLoss()  # 目标标签是one-hotted

# 开始训练
for epoch in range(EPOCH):
    for step, (b_x, b_y) in enumerate(train_loader):  # 分配batch data
        output = cnn(b_x)  # 先将数据放到cnn中计算output
        loss = loss_func(output, b_y)  # 输出和真实标签的loss，二者位置不可颠倒
        optimizer.zero_grad()  # 清除之前学到的梯度的参数
        loss.backward()  # 反向传播，计算梯度
        optimizer.step()  # 应用梯度

        if step % 50 == 0:
            test_output = cnn(test_x)
            pred_y = torch.max(test_output, 1)[1].data.numpy()
            accuracy = float((pred_y == test_y.data.numpy()).astype(int).sum()) / float(test_y.size(0))
            print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.numpy(), '| test accuracy: %.2f' % accuracy)

torch.save(cnn.state_dict(), 'cnn2.pkl')#保存模型
# 加载模型
cnn.load_state_dict(torch.load('cnn2.pkl'))
# 火力全开
cnn.eval()
# print 10 predictions from test data
inputs = test_x[:32]  # 测试32个数据
test_output = cnn(inputs)
pred_y = torch.max(test_output, 1)[1].data.numpy()
print(pred_y, 'prediction number')  # 打印识别后的数字
# print(test_y[:10].numpy(), 'real number')

img = torchvision.utils.make_grid(inputs)
img = img.numpy().transpose(1, 2, 0)
cv2.imshow('win', img)  # opencv显示需要识别的数据图片
key_pressed = cv2.waitKey(0)

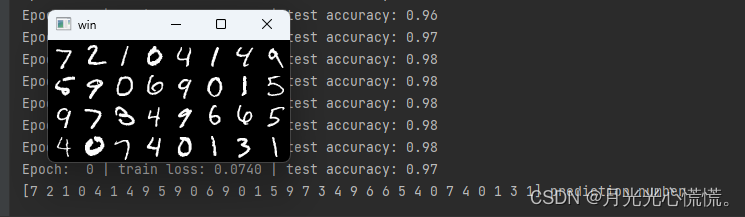
这个数据集是灰度图，只有一个通道，彩色图有3个通道。图像这块个人感觉最恶心就是维度。
个人经验：$[2000\ast 1\ast 28\ast 28]$，读这个数据要倒着看，2828是基本的数据单位，1是指由多少个$28\ast 28$构成一条数据，2000，就是有2000个128*28。如果是$[2000\ast 3\ast 28\ast 28]$，这个数据集理论上是3倍的$[2000\ast 1\ast 28\ast 28]$大小，表示用3个$28\ast 28$表示一条数据。