题目描述
某侦察队接到一项紧急任务,要求在A、B、C、D、E、F六个队员中尽可能多地挑若干人,但有以下限制条件:
1)A和B两人中至少去一人;
2)A和D不能一起去;
3)A、E和F三人中要派两人去;
4)B和C都去或都不去;
5)C和D两人中去一个;
6)若D不去,则E也不去。
问应当让哪几个人去?输出格式
要派出的人
若有多个,按字母递增顺序排列,用逗号分开(含末尾逗号)样例输出
A,B,C,F,
思路
根据以下条件,可列出表格:
1A和B两人中至少去一人;
2A和D不能一起去;
3A、E和F三人中要派两人去;
4B和C都去或都不去;
5C和D两人中去一个;
6若D不去,则E也不去。
| 条件一 | 条件二 | 条件三 | 条件四 | 条件五 | 条件六 |
|---|---|---|---|---|---|
| A去B不去 | A去D不去 | AE去F不去 | BC都去 | C去D不去 | DE都不去 |
| A不去B去 | A不去D去 | AF去E不去 | BC都不去 | C不去D去 | DE都去 |
| AB都去 | AD都不去 | EF去A不去 | D去E不去 |
容易得出A,B,C之间的关系为:
1.A去,B,C都不去
2.A不去,B,,C都去
3.A,B,C都去
if(状态1||状态2||状态3){
//其他限制条件,继续筛选
}这样一来,本来6个人,每人两种状态有2的6次方:64种状态,现在变为
以或(||)为连接,A,B,C三人每人有两种状态,2^3+2^3+2^3,即3*2^3=24种
现在只有2,3,5,6四种限制了,即:
if(条件二&&条件三&&条件五&&条件六){
if(是最优解){
输出此时状态为去的人
}
}代码显示
1. 声明一个数组a[10],用a[0]的值来表示人员A的状态——若a[0]为‘0’代表A不去,a[0]为‘1’代表A去;
同理a[1]代表B的状态、a[2]代表C、a[3]代表D、a[4]代表E、a[6]代表F;
初始化数组a[10]中的元素全为0,即所有人的状态均为不去
| 数组 | a[0] | a[1] | a[2] | a[3] | a[4] | a[5] |
|---|---|---|---|---|---|---|
| 人员 | A | B | C | D | E | F |
| 状态 | 0 | 0 | 0 | 0 | 0 | 0 |
ABC状态为3种:
| 数组 | a[0] | a[1] | a[2] |
|---|---|---|---|
| 人员 | A | B | C |
| 状态1 | 1 | 0 | 0 |
| 状态2 | 0 | 1 | 1 |
| 状态3 | 1 | 1 | 1 |
状态一:a[0]+a[1]+a[2]=1,状态二:a[0]+a[1]+a[2]=2,状态三:a[0]+a[1]+a[2]=3
for(i=1;i<4;i++){
if(i==1){
//A、B、C的值为状态1时的值1、0、0
a[0]=1;
a[1]=0;//由于初始化数组元素全为0,这里a[1]和a[2]的赋值也可以省去
a[2]=0;
}
if(i==2){
//A、B、C的值为状态2时的值0、1、1
}
if(i==3){
//A、B、C的值为状态3时的值1、1、1
}
//其他限制条件
}现在只需要对D,E,F的两种状态进行遍历:
for(i=1;i<4;i++){
if(i==1){
//A、B、C的值为状态1时的值1、0、0
a[0]=1;
a[1]=0;//由于初始化数组元素全为0,这里a[1]和a[2]的赋值也可以省去
a[2]=0;
}
if(i==2){
a[0]=0;
a[1]=1;
a[2]=1;
}
if(i==3){
a[0]=1;
a[1]=1;
a[2]=1;
}
for(a[3]=0;a[3]<2;a[3]++){//D的两种状态
for(a[4]=0;a[4]<2;a[4]++){//E的两种状态
for(a[5]=0;a[5]<2;a[5]++){//F的两种状态
if(条件2&&条件3&&条件5&&条件6){
if(最优解){
//输出即可
}
}
}
}
}
}得到24种状态分别为:
#include<stdio.h>
int main(void){
int a[10]={0};
int b[10]={0};
int i,j;
int mark=1;
for(i=1;i<4;i++){//根据第一个和第四个条件可得,A、B、C的可能组合有三种
if(i==1){
a[0] = 1;
}else if(i==2){
a[0] = 0;
a[1] = 1;
a[2] = 1;
}else{
a[0] = 1;
a[1] = 1;
a[2] = 1;
}
for(a[3]=0;a[3]<2;a[3]++){
for(a[4]=0;a[4]<2;a[4]++){
for(a[5]=0;a[5]<2;a[5]++){
printf("第%2d种:",mark);
for(j=0;j<6;j++){
printf("%d ",a[j]);
}
mark++;
printf("\n");
}
}
}
}
return 0;
}
得:
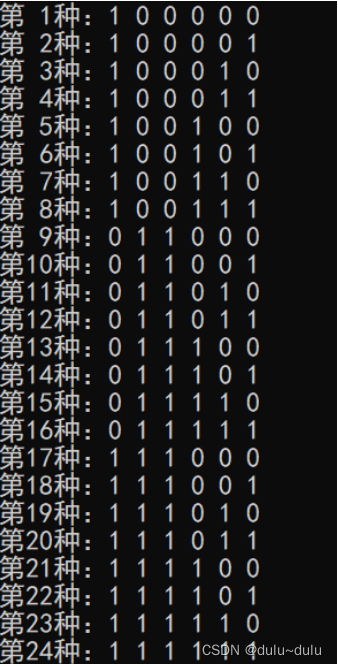
接下来是限制条件二,三,五,六:
| 条件二 | 条件三 | 条件五 | 条件六 |
|---|---|---|---|
| A去D不去 | AE去F不去 | C去D不去 | DE都不去 |
| A不去D去 | AF去E不去 | C不去D去 | DE都去 |
| AD都不去 | EF去A不去 | D去E不去 |
条件二:((a[0]==1&&a[3]==0)||(a[0]==0&&a[3]==1)||(a[0]==0&&a[3]==0))
条件三:((a[0]==1&&a[4]==1&&a[5]==0)||(a[0]==1&&a[4]==0&&a[5]==1)||(a[0]==0&&a[4]==1&&a[5]==1))
条件五:((a[2]==1&&a[3]==0)||(a[2]==0&&a[3]==1))
条件六:((a[3]==0&&a[4]==0)||(a[3]==1&&a[4]==0)||(a[3]==1&&a[4]==1)))
在比较哪一种条件下sum最多:
//求得最优解
for(j=0;j<6;j++){
sum1 += a[j];
}
if(sum1>sum2){//筛选人数最多的解
sum2 = sum1;
for(j=0;j<6;j++){
b[j] = a[j];
}
}最后得到代码为:
#include<stdio.h>
int main(void){
int a[10]={0};
int b[10]={0};
int i,j,sum1,sum2;
sum1=sum2=0;
//int mark=1;
for(i=1;i<4;i++){//根据第一个和第四个条件可得,A、B、C的可能组合有三种
if(i==1){
a[0] = 1;
}else if(i==2){
a[0] = 0;
a[1] = 1;
a[2] = 1;
}else{
a[0] = 1;
a[1] = 1;
a[2] = 1;
}
for(a[3]=0;a[3]<2;a[3]++){
for(a[4]=0;a[4]<2;a[4]++){
for(a[5]=0;a[5]<2;a[5]++){
/*
printf("第%2d种:",mark);
for(j=0;j<6;j++){
printf("%d ",a[j]);
}
mark++;
printf("\n");
*/
if(((a[0]==1&&a[3]==0)||(a[0]==0&&a[3]==1)||(a[0]==0&&a[3]==0))&&
((a[0]==1&&a[4]==1&&a[5]==0)||(a[0]==1&&a[4]==0&&a[5]==1)||(a[0]==0&&a[4]==1&&a[5]==1))&&
((a[2]==1&&a[3]==0)||(a[2]==0&&a[3]==1))&&
((a[3]==0&&a[4]==0)||(a[3]==1&&a[4]==0)||(a[3]==1&&a[4]==1))){
for(j=0;j<6;j++){
sum1 += a[j];
}
if(sum1>sum2){//筛选人数最多的解
sum2 = sum1;
//printf("符合条件的组合:");
for(j=0;j<6;j++){
b[j] = a[j];
//printf("%d ",b[j]);
}
//printf("\n");
}
}
}
}
}
}
if(b[0]==1){
printf("A,");
}
if(b[1]==1){
printf("B,");
}
if(b[2]==1){
printf("C,");
}
if(b[3]==1){
printf("D,");
}
if(b[4]==1){
printf("E,");
}
if(b[5]==1){
printf("F,");
}
return 0;
}最后可得到正确的输出啦!