一、图像翻转

图像翻转不等同于旋转，类似于一些视频的拍摄，拍摄后实际是左右颠倒的，通过图像翻转可进行还原

案例代码如下:

# 图片翻转
filpCode = 0表示上下翻转
flipCode > 0表示左右翻转
flipCOde < 0表示上下+左右翻转
new_first = cv2.flip(first,flipCode=-1)

二、图像旋转

函数原型：

rotate（img，rotateCode）

案例代码如下:

# 图片旋转
ROTATE_90_CLOCKWISE 90度顺时针
ROTATE_180 180度
ROTATE_90_COUNTERCLOCKWISE 90度逆时针

new_first = cv2.rotate(first,rotateCode= cv2.ROTATE_90_COUNTERCLOCKWISE)
# 展示图片
cv2.imshow('first',new_first)

三、仿射变换之平移

函数原型：

warpAffine（src，M，dsize，flags，mode，value）

M：变换矩阵
dsize：输出尺寸大小
flags：与size中的插值算法一致
mode：边界外推法标志
value：填充边界的值

案例代码如下:

# 读取图片
first = cv2.imread('5.jpg')

h,w,ch = first.shape

# 右移200个单位
# 变换矩阵(最少为float32位)
M = np.float([[1,0,200],[0,1,0]])

# 平移操作
# 注意opencv中先宽度，后高度
new_first = cv2.warpAffine(first,M,dsize=(w,h))

cv2.imshow('new_first',new_first)

四、仿射变换之获取变换矩阵

获取变换矩阵M的两种方法：

1、getRotationMatrix2D（center，angle，scale）

center：中心点
angle：旋转角度（逆时针）
scale：缩放比例（宽高同时缩放）

案例代码如下:

h,w,ch = first.shape
# 获取变换矩阵(注意旋转角度为逆时针)
# M = cv2.getRotationMatrix2D((100,100),15,1.0)

# 以图像中心点旋转
M = cv2.getRotationMatrix2D((w/2,h/2),15,1.0)

new_first = cv2.warpAffine(first,M,(w,h))

2、getAffineTransform（src[]，dst[]）

定义：通过点对应找到变换矩阵，一般三个点就可以；

拓展：这里可以联想到TPS算法，也是通过对应点进行变换的一种方法，二者可能有想通之处；

案例代码如下:

h,w,ch = first.shape

src = np.float32([[200,100],[300,100],[200,300]])
dst = np.float32([[100,150],[360,200],[280,120]])

# 通过三个点来确定变换矩阵
M = cv2.getAffineTransform(src,dst)
new_first = cv2.warpAffine(first,M,(w,h))

五、仿射变换之透视变换

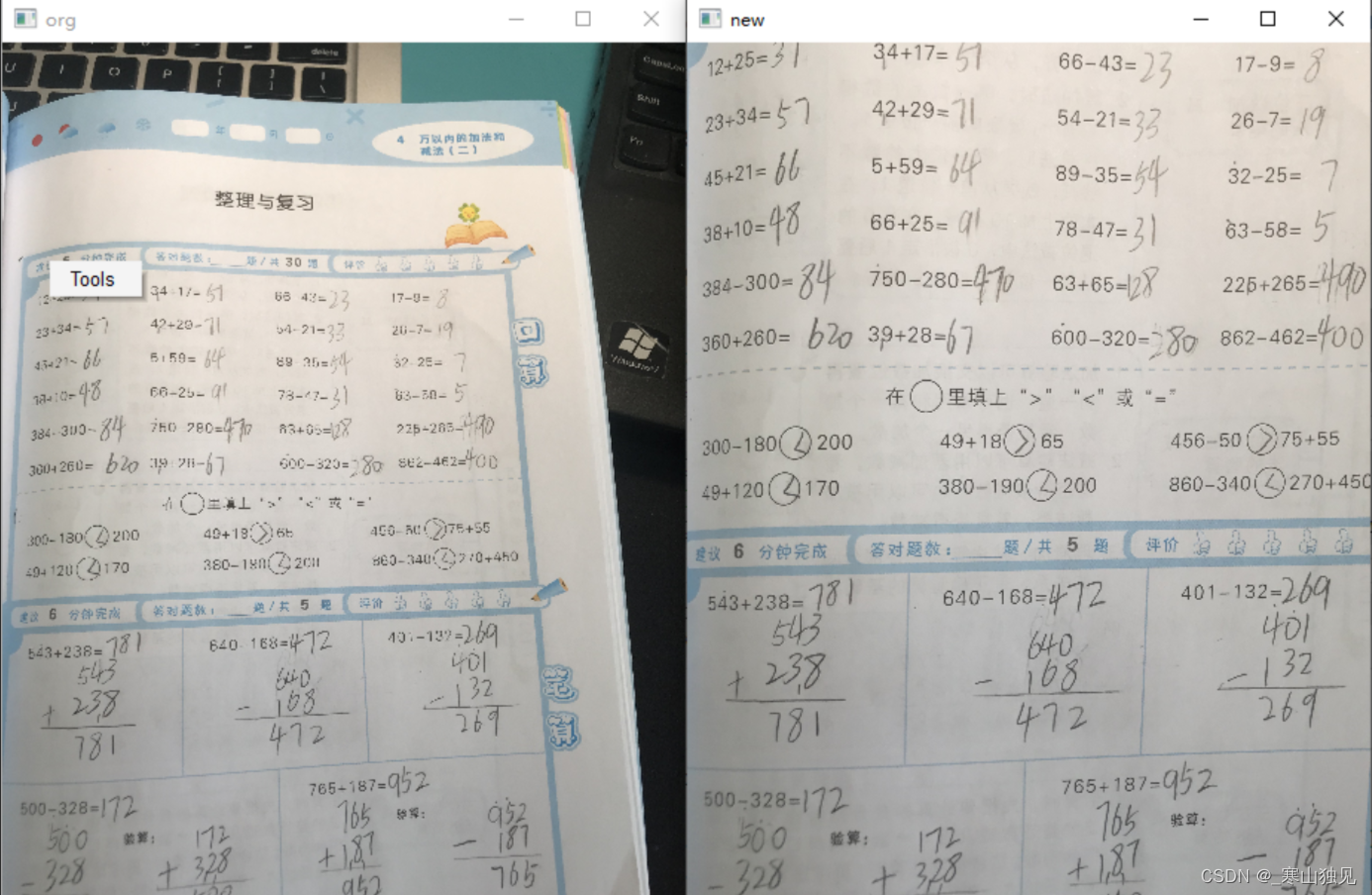
这里用一个具体案例来介绍，例如拍照搜题的软件，当拍摄整页时会有一种书本和桌面组合的样子，经过透视变换后能更好的将想要的信息放在图像中；

仿射变换函数原型：

warpPerspective（img，M，dsize，…）

获取变换矩阵函数原型：

getPerspective（src，dst）：和getAffineTransform函数比较类似，不同的是需要四个坐标点（图形四个角）；
案例代码如下:

# 获取变换矩阵
# src是原图的四个坐标
# dst
src = np.float32([[100,1100],[210,110],[0,4000],[2500,3900]])
dst = np.float32([[0,0],[2300,0],[0,3000],[2500,3000]])

M = cv2.getPerspectiveTransform(src,dst)

# 透视变换
new_img = cv2.warpPerspective(img,M,(2300,3000))

cv2.imshow('new_img',new_img)
cv2.waitKey(0)
cv2.destroyAllWindows()

运行结果如下: