目录
描述
输入描述:
输出描述:
解题过程
提交代码
递归方法
动态规划方法
学习代码
递归方法
动态规划方法
收藏点
描述
把m个同样的苹果放在n个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?
注意:如果有7个苹果和3个盘子,(5,1,1)和(1,5,1)被视为是同一种分法。
数据范围:0≤m≤10 ,1≤n≤10 。
输入描述:
输入两个int整数
输出描述:
输出结果,int型

解题过程
考察的是递归和动态规划,但是无论是前者和后者都没什么思路。所以就两种方法分别进行了学习,有不少收获。
发出一个疑问:我写的;大佬写的:
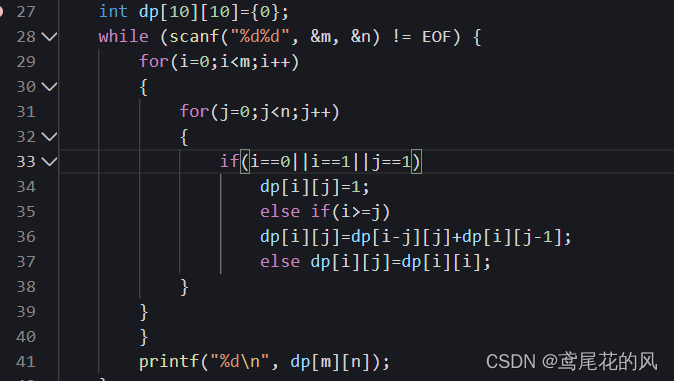

我们两个人定义的数组长度不同,循环的次数也不一样,我也成功实现了。所以大佬这么写是因为动态规划的格式就是这样,还是只是因为防溢出?
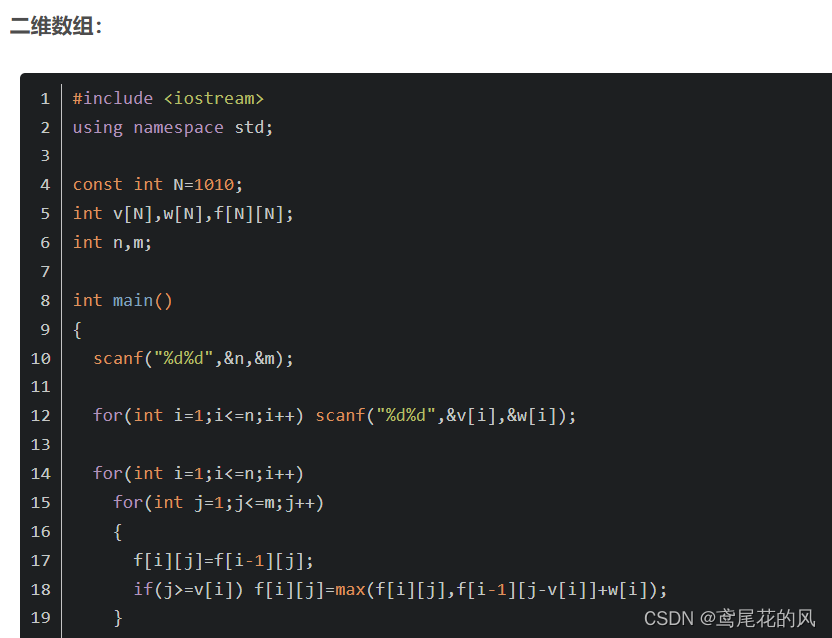
解答:↑应该是格式。。所以我可能需要换一种写法,虽然我这么写也不错。
(截图中代码来源于:动态规划:01背包问题_anieoo的博客-CSDN博客_01背包问题)
提交代码
经过学习——
递归方法
#include <stdio.h>
//递归方法
int func(int m,int n)//苹果个数是m,盘子个数是n
{
if(m==0||n==1)
return 1;//如果只剩一个盘子,或者没有苹果的话,那么就只有一种分法。
else if(m<n)
return func(m,m);//如果苹果数小于盘子数,那就相当于把m个苹果在m个盘子里进行排列组合
else
return func(m-n,n)+func(m,n-1);
//如果苹果数多于盘子数,那要考虑两种情况:1. 每个盘子都有苹果;2. 1到(n-1)个盘子里有苹果。
//如果苹果数多于盘子数,结果是两种情况相加。
}
int main() {
int a,b;
while (scanf("%d %d", &a, &b)!= EOF) {
printf("%d\n",func(a,b));
}
return 0;
}动态规划方法
(见“解题过程”部分。)
#include<stdio.h>
//动态规划方法
int main() {
int m,n,i,j;
int dp[10][10]={0};
while (scanf("%d%d", &m, &n) != EOF) {
for(i=0;i<=m;i++)
{
for(j=0;j<=n;j++)
{
if(i==0||i==1||j==1)
dp[i][j]=1;
else if(i>=j)
dp[i][j]=dp[i-j][j]+dp[i][j-1];
else dp[i][j]=dp[i][i];
}
}
}
printf("%d\n", dp[m][n]);
}学习代码
递归方法
(来源:https://blog.nowcoder.net/n/c9bc6821b3cd469b9cdb56469809e946;https://blog.nowcoder.net/n/38a41ddd60834504a98c7afb2ee2bbbd)
设f(m,n)为m个苹果,n个盘子的放法数目,则先对n作讨论,
当m<n:必定有n-m个盘子永远空着,去掉它们对摆放苹果方法数目不产生影响,即if(n>m) f(m,n) = f(m,m) 问题变成m个苹果,m个盘子的问题。也就是下面的m>=n的情况
当m>=n:不同的放法可以分成两类:
1、有至少一个盘子空着,原则上相当于f(m,n) = f(m,n-1) + f(m,n-2) + f(m,n-3)... 但是考虑到f(m,n-2)包含在f(m,n-1)中(这里思考下!),避免重复统计,则f(m,n) = f(m,n-1)
2、所有盘子都有苹果,相当于可以从每个盘子中拿掉一个苹果,不影响不同放法的数目,即f(m,n) = f(m-n,n).
则总的放苹果的放法数目等于两者的和,即 f(m,n) =f(m,n-1)+f(m-n,n)
递归出口条件说明: 当n=1时,所有苹果都必须放在一个盘子里,所以返回1; 当m=0时,没有苹果可以放置,返回1种放法; 递归的两条路,第一条n会逐渐减少,终会到达出口n==1; 第二条m会逐渐减少,因为n>m时,我们会return f(m,m) 所以终会到达出口m==0.
动态规划方法
(来源:https://blog.nowcoder.net/n/8a9de2612ce8433b8000be99745e81dd)
#include<stdio.h>
int main() {
int m, n;
int dp[11][11] = { 0 };
while (scanf("%d%d", &m, &n) != EOF) {
for (int i = 0; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (i == 0 || i == 1 || j == 1) {
dp[i][j] = 1;
} else if (i >= j) {
dp[i][j] = dp[i - j][j] + dp[i][j - 1];
} else {
dp[i][j] = dp[i][j - 1];
}
}
}
printf("%d\n", dp[m][n]);
}
}
收藏点
1. 递归和动态规划都要复习到。