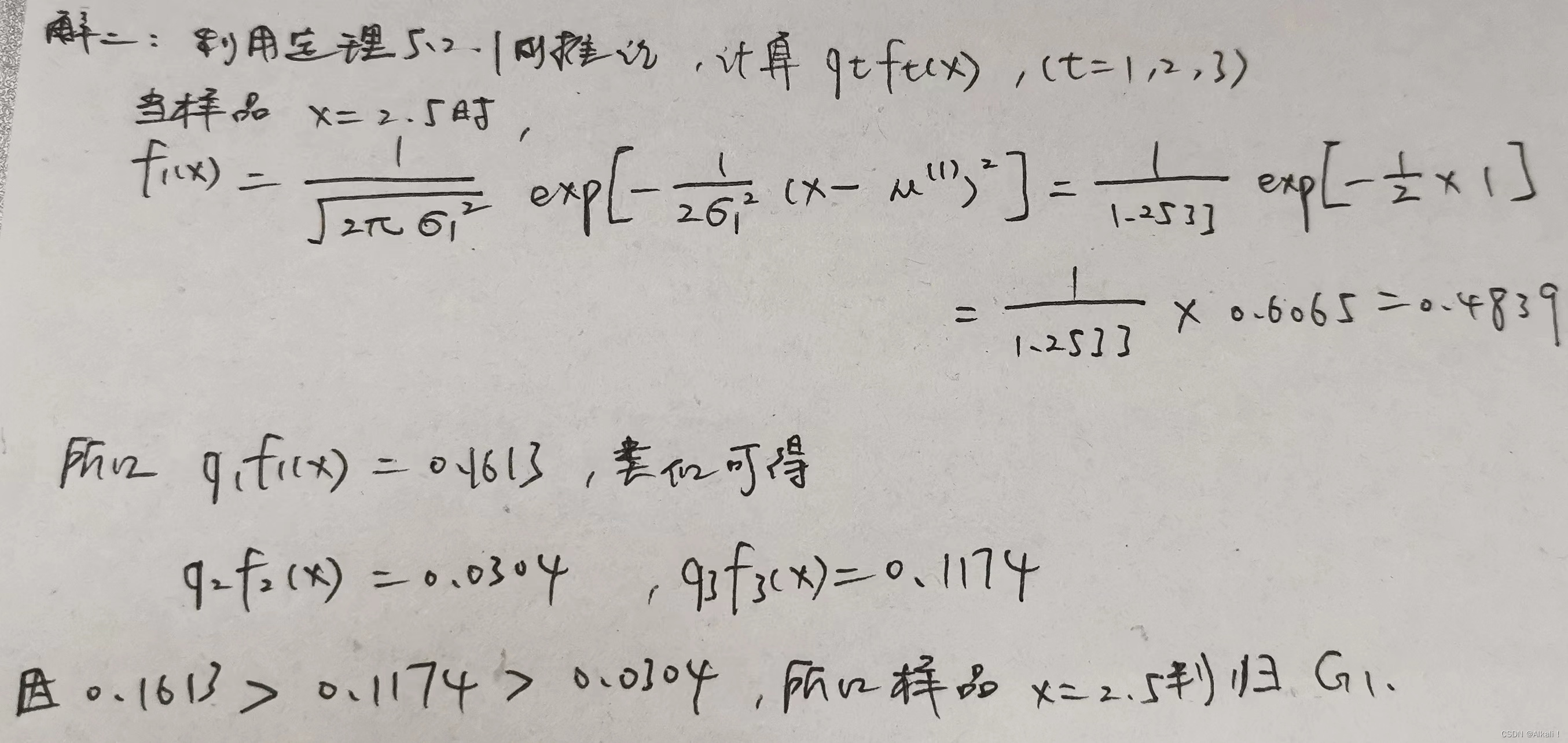5-2
题目

理论基础
-
多总体的距离判别
马氏距离: d G 2 ( x ) = ( x − μ ) 2 σ 2 d^{2}_{G}(x)=\frac{(x-\mu)^{2}}{\sigma^{2}} dG2(x)=σ2(x−μ)2

取马氏距离最小的那一个,就属于这类。 -
贝叶斯判别准则
-
计算 q t × f t ( x ) q_{t}\times f_{t}(x) qt×ft(x)
f t ( x ) = 1 2 π σ t 2 × e − 1 2 σ t 2 ( x − μ t ) 2 f_{t}(x)=\frac{1}{\sqrt{2\pi \sigma_{t}^{2}}} \times e^{-\frac{1}{2\sigma_{t}^{2}}(x-\mu_{t})^{2}} ft(x)=2πσt21×e−2σt21(x−μt)2
q t q_{t} qt 题目会给定
比哪个算下来的结果更大,哪个总体算下来大,就判规哪个 -
后验概率判别法
p ( t ∣ x ) = q t × f t ( x ) ∑ i = 1 n q i × f i ( x ) p(t|x)=\frac{q_{t}\times f_{t}(x)}{\sum_{i=1}^{n}q_{i}\times f_{i}(x)} p(t∣x)=∑i=1nqi×fi(x)qt×ft(x)
(n为总体的数量)
比哪个算下来的结果更大,哪个总体算下来大,就判规哪个
具体解题

(2)