目录
🍉什么是动态规划?
1)题目解析,(我们以第N个泰波那契数来进行举例)
2)解读算法原理
🍉第N个泰波那契数的代码编写
🍉空间优化
🍉什么是动态规划?
动态规划就是一种解决题目的总体思路,在秋招和春招的时候会有很多面试题都会用到动态规划的求解思路,我们就来仔细的学习以下~
1)题目解析,(我们以第N个泰波那契数来进行举例)
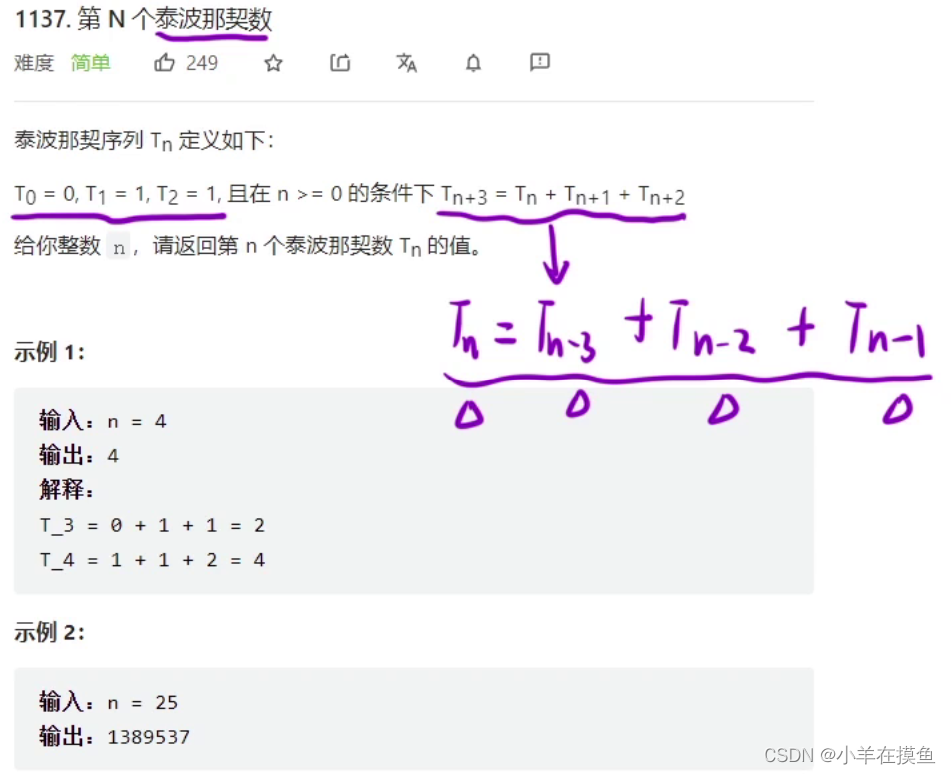
2)解读算法原理
🍒1.状态表示
什么是状态标识?我们先来问问chatGPT,得到以下解释:
在动态规划中,状态表示指的是如何表示子问题的状态。这些状态通常用变量或数组来表示,并且它们存储着问题的某种属性或者是解的部分信息。
具体的状态表示方法取决于问题的特点和要求。一般来说,状态表示应该满足以下两个条件:
- 无后效性:即一个状态的值只与前面的状态有关,与未来的状态无关。这意味着在计算每个状态时,不需要考虑当前状态之后的任何状态。这样可以简化计算过程并减小时间复杂度。
- 最优子结构:即全局最优解包含了各个子问题的最优解。这意味着通过计算子问题的最优解,可以推导出整个问题的最优解。
常见的状态表示方式包括但不限于:
- 单个变量:例如表示位置、时间等。
- 数组:例如表示数量、容量等。
- 矩阵:多维数组,用于表示相关的状态。
在动态规划问题中,选择合适的状态表示方法对于问题的求解至关重要。通过合理的状态表示,可以将复杂的问题转化为易于理解和计算的子问题,从而提高求解效率
简单来说:
我们会建立一个一维数组,我们称为dp表,然后我们把这个dp表想办法填满,填满之后,里面的某个值可能就是我们的最终结果,状态表示就是指,dp表里面的值所表示的含义
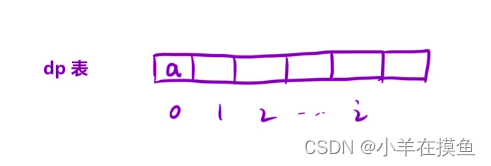
怎么来?
- 1.题目要求——dp[i]表示:第i个泰波那契数的值
- 2.经验+题目要求(多做题就会有所体会)
- 3.分析问题的过程中,发现重复子问题
🍒2.状态转移方程(最难的一步)
这个通过读题就可以看出,题目中已经告诉了我们:
dp[i] = dp[i-1] + dp[i-2] + dp[i-3]
具体如何推导,我们之后慢慢做题来看
🍒3.初始化
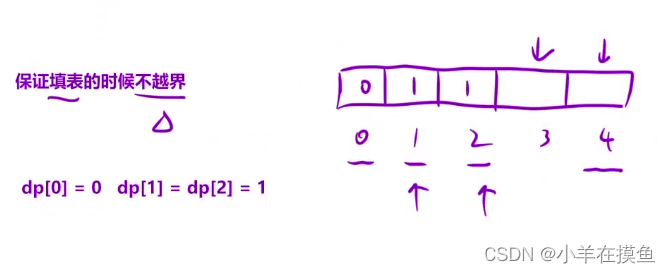
初始化的时候保证填表不越界,
比如泰波那契数这个题,我们要填表中的前三个,按公式来说我们就要直到第-3,-2,-1个位置
但这样肯定是越界的,所以我们要根据题目推出来。而这个题就已经给了我们前三个位置的数,分别为:0,1,1
🍒4.填表顺序
为了填写当前状态的时候,所需要的状态已经计算过了
在这道题里,我们的填表顺序是从左到右
🍒5.返回值
题目要求 + 状态表示
🍉第N个泰波那契数的代码编写
题目链接:力扣

class Solution {
public:
int tribonacci(int n)
{
// 1.创建 dp 表
// 2. 初始化
// 3. 填表
// 4. 返回值
if(n == 0)
return 0;
if(n == 1 || n == 2)
return 1;
vector<int> dp(n + 1);
dp[0] = 0,dp[1] = 1,dp[2] = 1;
for(int i = 3; i <= n; i++)
dp[i] = dp[i-1] + dp[i-2] + dp[i-3];
return dp[n];
}
};🍉空间优化
空间优化方法会在这道题和很后面学的背包问题中进行讲解
主要是因为我们刚刚接触到动态规划,先要把重点放在前五个步骤上面
(1.状态表示;2.状态转移方程;3.初始化;4.填表顺序;5.返回值)
空间优化会着重在背包问题的文章中重点讲解
我们先来了以这道题来了解以下空间优化
我们可以用到滚动数组的方法来进行优化
我们在求某一个状态的时候,仅仅只需要直到前面的三种状态即可,
我们在求 n=4 的时候,就不会在用到0位置的数,我们在求 n=5 的时候就不会用到 0和 1位置的值所以我们在求后面的数的时,只需要前面若干个数的时候,就可以用滚动数组来求解
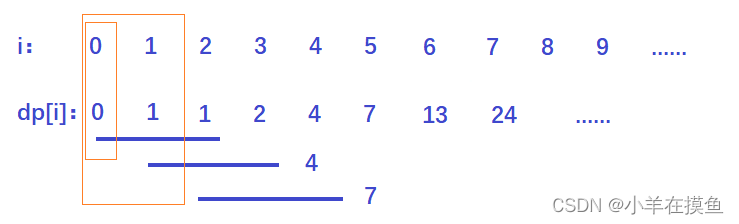
其时间复杂度:优化前时O(n^2),优化后时O(n);优化前时O(n),优化后时O(1)
🍒解决该题的思路:
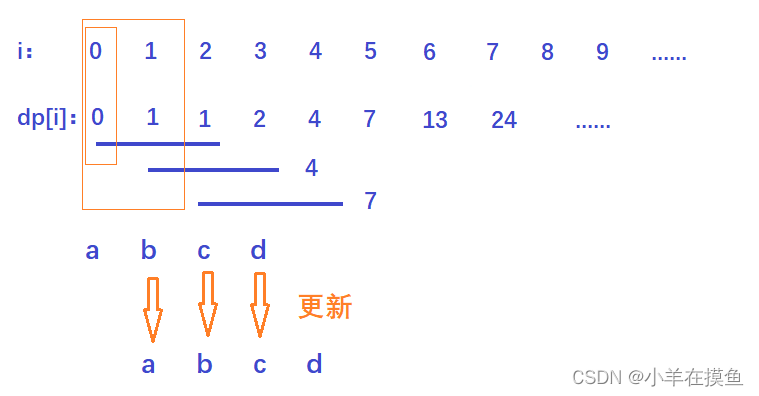
定义四个变量,每次对其进行更新操作
注意一个细节,我们注意赋值的顺序!
class Solution {
public:
int tribonacci(int n)
{
// 1.创建 dp 表
// 2. 初始化
// 3. 填表
// 4. 返回值
if(n == 0)
return 0;
if(n == 1 || n == 2)
return 1;
int a = 0, b = 1, c = 1, d = 0;
for(int i = 3; i <= n; i++)
{
d = a + b + c;
// 滚动操作
a = b;
b = c;
c = d;
}
return d;
}
};