目录

1、轮转数组

2、买卖股票的最佳时机

3、买卖股票的最佳时机②

4、跳跃游戏

5、跳跃游戏2

6、最大子序列交替和

7、交替数字和

8、下降路径最小和

---

1、轮转数组

class Solution():
    def rotate(self, nums, k):
        def reverse(i, j):    #逆置数组
            while i < j:
                nums[i], nums[j] = nums[j], nums[i]
                i += 1
                j -= 1
            return
        n = len(nums)
        k %= n            #必须要取模运算，因为要考虑到k的值有可能比n的值要大
        reverse(0, n-1)   #首先将整个数组逆置
        reverse(0, k-1)   #将左边k个元素逆置
        reverse(k, n-1)   #再将右边n-k个元素逆置
#这样一来就能实现轮转的目标

2、买卖股票的最佳时机

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        minprice = float('inf')
        maxprofit = 0
        for price in prices:   #遍历整个数组
            minprice = min(minprice, price)   #记录下最小价格，因为在遍历后面的元素的时候，肯定是要跟前面的最小的去减的
            maxprofit = max(maxprofit, price - minprice)    #比较我当前已经得到的最大收益和我即将可以算得的最大收益，取最大的
        return maxprofit

3、买卖股票的最佳时机②

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        profit = 0
        for i in range(1, len(prices)):
            temp = prices[i] - prices[i-1]
            if temp > 0:    #后一项减去前一项，只有temp为正的时候才证明股票是上涨的
                profit += temp
        return profit 

4、跳跃游戏

class Solution:
    def canJump(self, nums: List[int]) -> bool:
            n = len(nums)
            furthest = nums[0]        #一上来最远的可以跨越nums[0]的元素大小的长度
            for i in range(1, n):
                if i > furthest:      #如果下标比能跨越的最大长度要大，直接返回否,因为根本来不了这个下标
                    return False
                if i + nums[i] > furthest:   #在这个位置可以跨越的最大位置比最长能跨越的距离大，则修改最长跨越距离
                    furthest = i + nums[i]
                if furthest >= n-1:      #能跨越的最大距离为整个数组，直接就成了
                    return True
            return furthest >= n-1    #等所有都结束，看能跨越的最长距离是不是整个数组，不是则表明失败

5、跳跃游戏2

class Solution:
    def jump(self, nums: List[int]) -> int:
        #贪心法
        end = 0     #表示当前一步能跳的边界
        max_pos = 0    #表示几种可能里面的最大位置
        steps = 0      #表示跳跃次数
        for i in range(len(nums) - 1):      
            #i表示下标
            max_pos = max(max_pos, nums[i] + i)
            if i == end:
                end = max_pos   #边界到达了最大位置
                steps += 1
        return steps

6、最大子序列交替和

#2023.7.11
class Solution:
    def maxAlternatingSum(self, nums: List[int]) -> int:
        n = len(nums)
        f = [0] * (n + 1)
        g = [0] * (n + 1)
        for i, x in enumerate(nums, 1):
            f[i] = max(g[i - 1] - x, f[i - 1])
            g[i] = max(f[i - 1] + x, g[i - 1])
        return max(f[n], g[n])

7、交替数字和

class Solution:
    def alternateDigitSum(self, n: int) -> int:
        sign, ans = 1, 0      #首先将标志记为1，因为第一位取正号；将最终答案记为0，依次运算相加
        for s in str(n):    #挨个取出字符
            num = int(s)    #定义整型
            ans += num * sign   #计算相加
            sign = -sign    #标志位取相反数
        return ans

8、下降路径最小和

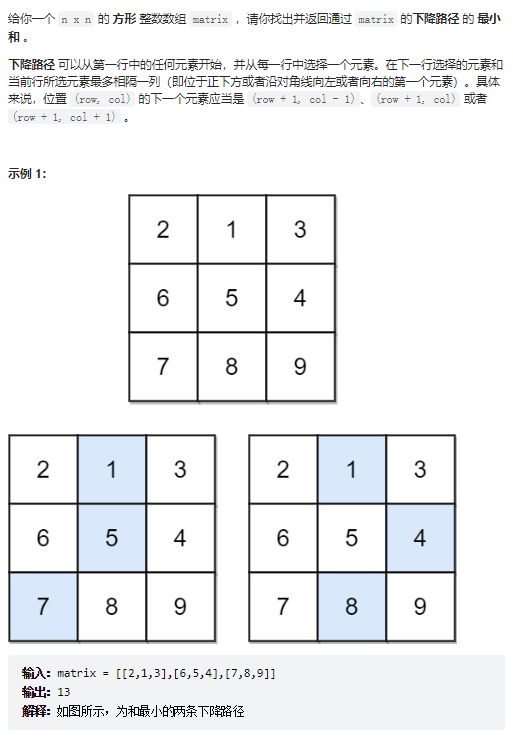
class Solution:
    def minFallingPathSum(self, matrix: List[List[int]]) -> int:
        n = len(matrix)       # n为方阵大小
        fall_sum = [[0]*n for _ in range(n)]       # 定义状态转移矩阵
        # 首行的下降路径最小和为首行元素本身
        for j in range(n):
            fall_sum[0][j] = matrix[0][j]
        # 从第二行开始生成状态矩阵
        for i in range(1,n):
            for j in range(n):
                fall_sum[i][j] = fall_sum[i-1][j]      # 初始为上一行的下降路径最小和
                if j - 1 >= 0:
                    fall_sum[i][j] = min(fall_sum[i][j], fall_sum[i - 1][j - 1])     # 左一列存在，和上一行的左一列比较
                if j + 1 < n:
                    fall_sum[i][j] = min(fall_sum[i][j], fall_sum[i - 1][j + 1])      # 右一列存在，和上一行的右一列比较、
                fall_sum[i][j] += matrix[i][j]        # 上一行三个位置的最小值加上当前位置元素值
        return min(fall_sum[n - 1])           # 从最后一行中找到下降路径最小和