文章目录
- 参考:
- 总结
- 大纲要求
- 搜索算法-广度优先搜索
- 迷宫问题
- 问题
- 迷宫的存储
- 迷宫的移动
- 搜索方式
- 代码实现
- 图的广度优先遍历
- 题目描述
- 用邻接矩阵表示图
- 搜索算法-广度优先搜索

参考:
【算法设计】用C++类和队列实现图搜索的广度优先遍历算法
C/C++ 之 广度优先搜索
算法讲解之广度优先搜索
总结
本系列为C++算法学习系列,会介绍 算法概念与描述,入门算法,基础算法,数值处理算法,排序算法,搜索算法,图论算法, 动态规划等相关内容。本文为搜索算法部分。
大纲要求
【 5 】深度优先搜索
【 5 】广度优先搜索
搜索算法-广度优先搜索
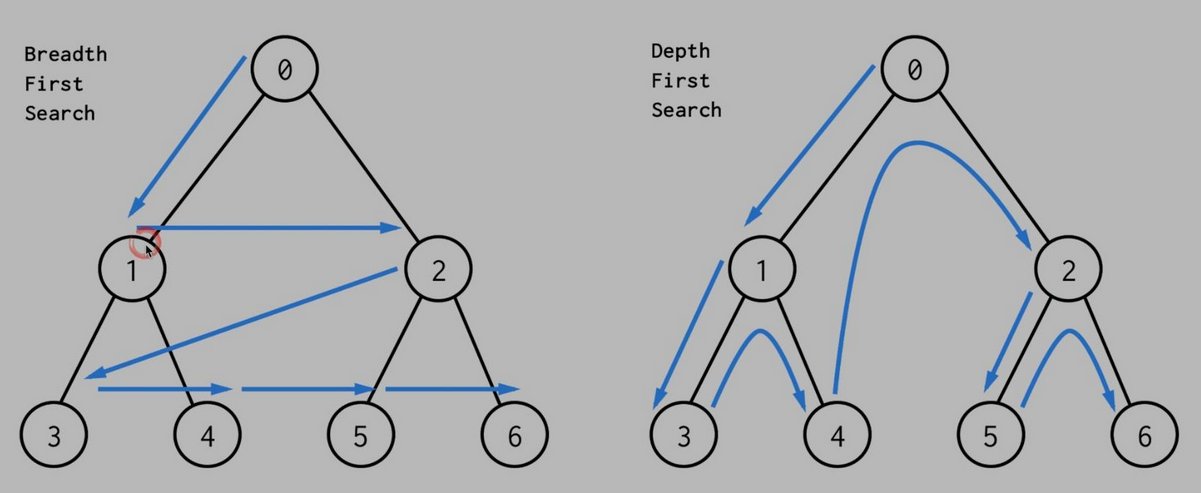
广度优先搜索(Breadth-First Search),又称作宽度优先搜索。BFS是一种完备策略,即只要问题有解,它就一定可以找到解。并且,广度优先搜索找到的解,还一定是路径最短的解。但是它盲目性较大,尤其是当目标节点距初始节点较远时,将产生许多无用的节点,因此其搜索效率较低。一般只有需求最优解的时候会用BFS。
广度优先搜索算法(又称宽度优先搜索)是最简便的图的搜索算法之一,这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。
广度优先算法的核心思想是:从初始节点开始,应用算符生成第一层节点,检查目标节点是否在这些后继节点中,若没有,再用产生式规则将所有第一层的节点逐一扩展,得到第二层节点,并逐一检查第二层节点中是否包含目标节点。若没有,再用算符逐一扩展第二层的所有节点……,如此依次扩展,检查下去,直到发现目标节点为止。即
⒈从图中的某一顶点V0开始,先访问V0;
⒉访问所有与V0相邻接的顶点V1,V2,…,Vt;
⒊依次访问与V1,V2,…,Vt相邻接的所有未曾访问过的顶点;
⒋循此以往,直至所有的顶点都被访问过为止。
这种搜索的次序体现沿层次向横向扩展的趋势,所以称之为广度优先搜索。
int Bfs()
{
初始化,初始状态存入队列;
队列首指针head=0; 尾指针tail=1;
do
{
指针head后移一位,指向待扩展结点;
for (int i=1;i<=max;++i) //max为产生子结点的规则数
{
if (子结点符合条件)
{
tail指针增1,把新结点存入列尾;
if (新结点与原已产生结点重复) 删去该结点(取消入队,tail减1);
else
if (新结点是目标结点) 输出并退出;
}
}
}while(head<tail); //队列为空
}
迷宫问题
问题

现在有一个4*4的迷宫,李雷在迷宫的左上角,迷宫出口在右下角,李雷体力有限,他希望尽快走出迷宫,请你告诉李雷最少需要走多少步(每个格子不能重复走动)。
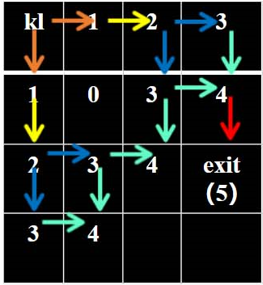
我们可以按照这样的思路去找:
1.从起点出发,检查第1步可以到达的所有点,判断是否为终点。
2.依次从第1步到达的点出发,检查判断第2步可以到达的点是否为终点。
3.依次从第2步到达的点出发,检查判断第3步可以到达的点是否为终点。
4.依次从第3步到达的点出发,检查判断第4步可以到达的点是否为终点。
5.依次从第4步到达的点出发,检查判断第5步可以到达的点是否为终点。
6.找到终点,程序结束,步数为5。
迷宫的存储

迷宫的移动

搜索方式
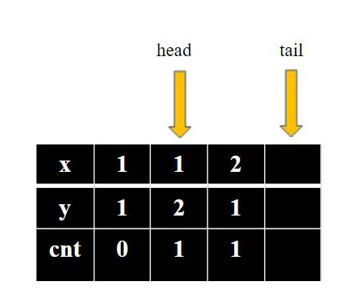
1.我们需要使用队列(que)来实现,用一个结构体表示每次找到的点的坐标信息以及步数(x,y,cnt)。
2将起点入队。
3.取出队首元素,队首后移(head++) ,将队首元素上下左右的四个点依次入队(步数cnt要+1),同时判断是否到达终点,若到达终点则终止程序。
4.重复步骤3,直到找到终点或者队列为空(即head>tail)
代码实现
#include<iostream>
using namespace std;
struct wz
{
int x,y;//坐标
int cnt;//步数
} que[1000],front,a;//front 用来存每次取出的队首元素,a存起点信息
int maze[5][5];// 迷宫信息
int used[5][5];//已经使用 一般为book
int fx[4][2] = {
{0,-1},//下
{0,1},//上
{-1,0},//左
{1,0}//右
};
int head=1;//队列的头
int tail=1;//队列的尾
int sx=1,sy=1;// sx起点 sy终点
int ex=3,ey=4;//终点的坐标
int flag=0;
void bfs(wz a);// 广度优先函数
int maze_data[5][5]={
{0,0,0,0,0},
{0,1,1,1,1},
{0,1,0,1,1},
{0,1,1,1,1},
{0,1,1,1,1}
};
int main()
{
for(int i=1;i<=4;i++)
{
for(int j=1;j<=4;j++)
{
maze[i][j]=maze_data[i][j];
// cout<<maze[i][j];
// cin>>maze[i][j];//填充迷宫
}
// cout<<endl;
}
a.x=sx;//存起点信息
a.y=sy;//存起点信息
a.cnt=0;//初始步数为0
bfs(a);//从a点开始搜索
cout<<" head"<<head<<" tail:"<<tail<<endl;
cout<<que[tail].cnt;//输出尾节点的步数
return 0;
}
void bfs(wz a)
{
que[head]=a;//起点入队
used[a.x][a.y]=1;//起点被使用
cout<<" head:"<<head<<" tail:"<<tail<<endl;
cout<<" que[head]:"<<que[head].x<<" "<<que[head].y <<" "<<que[head].cnt<<"used[a.x][a.y]:"<<used[a.x][a.y]<<endl;
while(head<=tail)//当head<tail表示队列不为空
{
cout<<"while循环内: head:"<<head<<"tail:"<<tail<<endl;
front = que[head];//取出队首
head++;//队首出队
for(int i=0;i<4;i++)//搜索队列当前节点的四个方向的点
{
int nx=front.x+fx[i][0];//搜索的nx坐标
int ny=front.y+fx[i][1];//搜索的ny坐标 下一个节点的坐标
// 下一个节点坐标不超出迷宫范围,未被走过,且不是障碍
if(nx>=1 && nx<=4 && ny>=1 &&ny<=4 && !used[nx][ny] && maze[nx][ny])
{
tail++;//把tail队尾后移,表示添加节点
used[nx][ny]=1;//标记走过
que[tail].x=nx;
que[tail].y=ny;
// 等价与que[++tail].x=nx
que[tail].cnt=front.cnt+1;//步数+1
cout<<"for循环 if内: nx:"<<nx<<"ny:"<<ny<<"cnt:"<<front.cnt+1<<endl;
}
if(nx==ex && ny==ey)
{
head=tail+1;//推出while循环
break;//推出for循环
}
}
}
}
图的广度优先遍历
题目描述
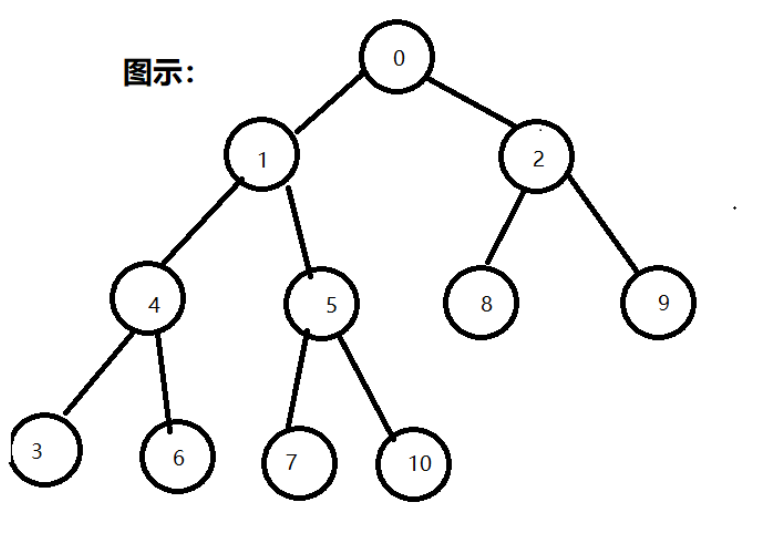
使用广度优先遍历算法输出访问结点的顺序,结果为0、1、2、4、5、8、9、3、6、7、10
用邻接矩阵表示图

按照案例给出的图,我简化成了这个邻接矩阵,画法就是,两个结点之间相连设置为T,不相连设置为F,规定结点自身与自身不相连,当然对T和F要有声明,例如 const bool T =true,F=false;这样T就代表通路,F就代表断路了
#include<iostream>
using namespace std;
const int n=11;// 结点个数
const int SIZE=10;
class queue
{
private:
int buffer[SIZE];//队列长度
int rear;//rear指向队尾
int head;//head 指向队列前一格
// 使得rear和head的指向向下进行
// 对10取余 得到个位数,
int update(int value)
{
return (value+1)%SIZE;
}
public:
// 无参构造,利用初始化列表给head和rear的初始化为0
queue():head(0),rear(0){}
// 判断队列是否为空
bool queueNull(){return rear == head;}
// 队满的判断 让rear和head的下标重置为0
bool queueMax(){return update(rear)==head;}
bool queueAdd(int E)
{
// 如果队满了就不添加
if(queueMax()) return false;
rear = update(rear);//更新队尾的指针,队尾指针+1
buffer[rear] = E; //把数据E插入到队列的队尾中
return true;
}
//区队首元素的方法
bool getFirstQueue(int& E)
{
//如果队空了,返回
if(queueNull()) return false;//
head = update(head);//更新队首指针
E = buffer[head];//取出队首
return true;
}
};
const bool F = false, T = true;
bool nextClose[n][n] = {
{F,T,T,F,F,F,F,F,F,F,F},
{T,F,F,F,T,T,F,F,F,F,F},
{T,F,F,F,F,F,F,F,T,T,F},
{F,F,F,F,T,F,F,F,F,F,F},
{F,T,F,T,F,F,T,F,F,F,F},
{F,T,F,F,F,F,F,T,F,F,T},
{F,F,F,F,T,F,F,F,F,F,F},
{F,F,F,F,F,T,F,F,F,F,F},
{F,F,T,F,F,F,F,F,F,F,F},
{F,F,T,F,F,F,F,F,F,F,F},
{F,F,F,F,F,T,F,F,F,F,F}
};
bool flag[n];
//假设begin为0结点
void BreadthFirstSearch(int begin)
{
for(int i=0;i<n;i++)
{
// 先把标志位flag数组全设置为false
flag[i]=false;
}
queue que; //创建队列对象
que.queueAdd(begin); // 把元素添加到队列中的第2个格子
flag[begin] = true;//把标记为设置为true
int node;
while(!que.queueNull())
{
que.getFirstQueue(node);
cout<<node<<",";
for(int i=0;i<n;i++)
{
if(nextClose[i]&&!flag[i])
{
que.queueAdd(i);
flag[i]=true;
}
}
}
}
int main()
{
BreadthFirstSearch(0);
cout<<"hello world"<<endl;
}
搜索算法-广度优先搜索
在深度优先搜索算法中,是深度越大的结点越先得到扩展。如果在搜索中把算法改为按结点的层次进行搜索,本层的结点没有搜索处理完时,不能对下层结点进行处理,即深度越小的结点越先得到扩展,也就是说先产生的结点先得以扩展处理,这种搜索算法称为广度优先搜索法。