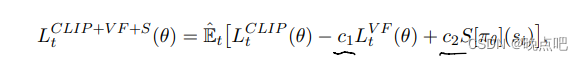「XKOI」Round 3 赛后题解

news2024/11/18 22:41:46

比赛链接：「XKOI」Round 3

本题解同步发表于

  • 洛谷：传送门

  • CSDN：传送门

文章目录

  • 比赛链接：[「XKOI」Round 3](https://www.luogu.com.cn/contest/117863)
  • A [T343985 CRH的工作](https://www.luogu.com.cn/problem/T343985)
      • 1.1 题意简述
      • 1.2 知识点
      • 1.3 解题思路
        • a. 暴力（30pts）
        • b. Treap（100pts）
        • c. STL set（100pts）
  • B [T350797 日记和她的小日记](https://www.luogu.com.cn/problem/T350797)
      • 2.1 题意简述
      • 2.2 涉及知识点
      • 2.3 解题思路
        • a. 骗分 （5pts）
        • b. 动态规划 （35pts）
        • c. 组合数学（70pts）
        • d. 组合数学 （100pts）
        • e. Lucas(Extra)
        • f. CRT(Extra)
  • C [T351142 只因字塔的探索](https://www.luogu.com.cn/problem/T351142)
      • 3.1 涉及知识点
      • 3.2 解题思路
        • a. 区间DP（100pts）
        • b. 记忆化搜索（100pts）
  • D [T352449 三体世界的毁灭](https://www.luogu.com.cn/problem/T352449)
      • 4.1 题意简述
      • 4.2 涉及知识点
      • 4.3 解题思路（100pts）

A T343985 CRH的工作

1.1 题意简述

求 ∑ i = 1 n min ⁡ 1 ≤ j < i ∣ a j − a i ∣ \sum_{i=1}^n \min_{1 \le j < i} |a_j - a_i| ∑i=1n​min1≤j<i​∣aj​−ai​∣

1.2 知识点

平衡树 Treap 找前驱后继、STL set

1.3 解题思路

a. 暴力（30pts）

这个不多讲，放个代码大家自己理解。

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e6 + 10;

int a[N];
int n;

int main()
{
	scanf("%d", &n);
	for (register int i = 0; i < n; i ++ )
		scanf("%d", &a[i]);
	
	int res = a[0];
	for (register int i = 1; i < n; i++)
	{
		int t = N;
		for (register int j = 0; j < i; j++)
			t = min(abs(a[i] - a[j]),t);
		res += t;
	}
	
	printf("%d\n", res);
	return 0;
}

b. Treap（100pts）

把当前天之前的所有数都加到Treap当中，然后每次累加与前驱和后继的差的最小值累加起来即可。

注：这种方法码量较大。

#include <iostream>
#include <cstdlib>

using namespace std;

typedef long long LL;

const int N = 33010;
const int INF = 1e7;

struct Treap
{
	int l, r;
	int key, val;
}tr[N];

int n, x;
int root, idx;

int get_node(int key)
{
	tr[ ++ idx].key = key;
	tr[idx].val = rand();
	return idx;
}

void build()
{
	get_node(INF), get_node(-INF);
	root = 1, tr[1].r = 2;
}

void zig(int &p)
{
	int q = tr[p].l;
	tr[p].l = tr[q].r, tr[q].r = p, p = q;
}

void zag(int &p)
{
	int q = tr[p].r;
	tr[p].r = tr[q].l, tr[q].l = p, p = q;
}

void insert(int &p, int key)
{
	if (!p) p = get_node(key);
	else if (tr[p].key == key) return;
	else if (tr[p].key > key)
	{
		insert(tr[p].l, key);
		if (tr[tr[p].l].val > tr[p].val) zig(p);
	}
	else
	{
		insert(tr[p].r, key);
		if (tr[tr[p].r].val > tr[p].val) zag(p);
	}
}

int get_prev(int p, int key)
{
	if (!p) return -INF;
	if (tr[p].key > key) return get_prev(tr[p].l, key);
	return max(tr[p].key, get_prev(tr[p].r, key));
}

int get_next(int p, int key)
{
	if (!p) return INF;
	if (tr[p].key < key) return get_next(tr[p].r, key);
	return min(tr[p].key, get_next(tr[p].l, key));
}

int main()
{
	LL res = 0;
	build();
	
	scanf("%d", &n);
	for (int i = 1; i <= n; i ++ )
	{
		scanf("%d", &x);
		if (i == 1) res += x;
		else res += min(x - get_prev(root, x), get_next(root, x) - x);
	    
	    insert(root, x);
	}
	
	printf("%lld\n", res);
	
	return 0;
}

c. STL set（100pts）

众所周知，set 能有序地维护同一类型的元素，但相同的元素只能出现一次。

对于这道题来说，我们可以用 set 来记录下之前出现过的所有营业额。

每次输入一个新的数 x x x 后，通过 lower_bound 操作找到 set 中大于等于 x x x 的第一个数。

  1. 如果这是第一个数，直接插入到 set 里。

  2. 这个数等于 x x x ,显然最小波动值为 0 0 0 ，我们也不需要再插入一个 x x x 放到 set 里了。

  3. 这个数大于 x x x ,通过 set 的特性可以很轻松的找到这个数的前驱，也就是小于 x x x 的第一个数。将两个数分别减去 x x x ,对绝对值取个 min ⁡ \min min 就好了。此时要将 x x x 插入到 set 中。

#include <iostream>
#include <set>

using namespace std;

const int INF = 2e9;

int n, x, ans;
set<int> S;
set<int>::iterator k, a;

int main()
{
	S.insert(INF), S.insert(-INF);
	
	scanf("%d", &n);
	for (int i = 1; i <= n; i ++ )
	{
		scanf("%d", &x);
		if (S.size() == 2)
		{
			ans += x;
			S.insert(x);
		}
		else
		{
			k = S.lower_bound(x);
			if (*k != x)
			{
				a = k;
				a -- ;
				ans += min(abs(*a - x), abs(*k - x));
				S.insert(x);
			}
		}
	}
	
	printf("%d\n", ans);
	
	return 0;
}

B T350797 日记和她的小日记

2.1 题意简述

n n n 个互不相同的物品需要放进 m m m 个盒子里，相邻的两个盒子不能都有物品，一个盒子最多放一个物品。求放的方案数。

2.2 涉及知识点

动态规划，组合数学 (排列数)，乘法逆元 (快速幂，费马小定理)

2.3 解题思路

a. 骗分 （5pts）

当 n = m = 1 n = m = 1 n=m=1 时，日记只能把这本小日记给这个小朋友，因此答案为 1 1 1。

b. 动态规划 （35pts）

前 7 7 7 个测试点的数据范围允许我们使用 O ( n 2 ) O(n^2) O(n2) 的做法，因此可以使用动态规划。

赠出小日记的顺序是没有意义的，所以我们可以钦定日记从第 1 1 1 个小朋友依次走到第 n n n 个小朋友，并选择是否赠出小日记。

同时，每次赠出的小日记的编号也是没有意义的。钦定第 i i i 个赠出的为第 i i i 本小日记，则
只需要把最终答案 ×   m ! \times\ m! × m! 即可。

记 d p i , j dp_{i,j} dpi,j​ 为日记刚刚走过第 i i i 个小朋友时共赠出 j j j 本小日记的方案数。

有两种转移方式：

  1. 日记不将小日记赠给第 i i i 个小朋友，此时 d p i , j = d p i − 1 , j dp_{i,j}=dp_{i-1,j} dpi,j​=dpi−1,j​；

  2. 日记将小日记赠给第 i i i 个小朋友，则第 i − 1 i − 1 i−1 个小朋友必然没有获得小日记，此时可以从 [ 1 , i − 2 ] [1, i − 2] [1,i−2] 里的任何一个人转移过来： d p i , j = d p i − 2 , j − 1 dp_{i,j}=dp_{i-2,j-1} dpi,j​=dpi−2,j−1​。

为什么第二种转移方式不需要求和呢？因为第一种转移方式已经考虑到前面的情况了。时间复杂度：每个状态只能从常数个状态转移过来，因此时间复杂度是 O ( n m ) O(nm) O(nm) 的。

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

const int maxn = 3005, maxm = 1505;
int T, n, m;
ll mod;
ll dp[maxn][maxm];

void solve()
{
	dp[0][0] = 1;
// 初始日记没有走过任何一个小朋友，当然也没有赠出任何一本小日记
	for (int i = 1; i <= n; ++i)
	{
		for (int j = 0; j <= m; ++j)

		{
			dp[i][j] = dp[i - 1][j];
			if (i >= 2) // 特别地，走过第一个小朋友时没有限制
				dp[i][j] += dp[i - 2][j - 1];
			else
				dp[i][j] += dp[i - 1][j - 1];
			if (dp[i][j] >= mod)
				dp[i][j] -= mod;
// debug(i, j, dp[i][j]);
		}
	}
	for (int i = 2; i <= m; ++i)
		dp[n][m] = dp[n][m] * i % mod;
}

int main()
{
	scanf("%d %lld", &T, &mod);
	while (T--)
	{
		scanf("%d %d", &n, &m);
		solve();
		printf("%lld\n", dp[n][m]);
	}
	return 0;
}

c. 组合数学（70pts）

动态规划没有办法适应更大的数据范围了。考虑要求计算的答案的组合意义。

相邻的两个小朋友不能都获得小日记，换句话说，若一个小朋友获得小日记，下一个小朋友就会被忽略。

注意，这不包含最后一个获得小日记的小朋友，因为他之后没有更多小朋友能获得小日记了。

所以，一共恰好忽略 ( m − 1 ) (m − 1) (m−1) 个小朋友。

忽略掉这些之后，题意变成了从 n − m + 1 n − m + 1 n−m+1 个小朋友里选 m m m 个赠送小日记，这就很好计算了。

注意每本小日记是不同的，所以我们使用排列数 A n − m + 1 m A_{n-m+1}^m An−m+1m​。

它的形式相当于 m 个数的连乘，但是不保证模数为质数，所以暴力计算。时间复杂度： O ( ∑ m O(\sum m O(∑m。

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

int T;
ll n, m, mod;

int main()
{
	scanf("%d %lld", &T, &mod);
	while (T--)
	{
		scanf("%lld %lld", &n, &m);
		ll ans = 1;
		for (int i = 1, cnt = n - m + 1; i <= m; ++i, --cnt)
		// 第i本小日记将有cnt种赠送方案
			ans = ans * cnt % mod;
		printf("%lld\n", ans);
	}
	return 0;
}

d. 组合数学 （100pts）

最后 30 30 30 分的数据范围比较大，但是模数是质数。

做法 c c c 的问题在于没有保证模数是质数，不能应用预处理。

但最后 30 30 30 分保证了这一点，所以可以预处理 m m m 范围内的 i ! i! i! 和 ( i ! ) − 1 (i!)^{−1} (i!)−1。

需要跟做法 c c c 拼一下，否则不能解决之前模数不是质数的测试点。

时间复杂度： O ( max ⁡ m ) O(\max m) O(maxm)。

#include <iostream>
#define int long long

using namespace std;

const int N = 4e6 + 10;

int T, P;
int n, m;
int f[N], uf[N];

bool is_prime(int n)
{
	if (n < 2) return false;
	for (int i = 2; i <= n / i; i ++ )
		if (n % i == 0) return false;
	return true;
}

int qpow(int a, int b, int p)
{
	int res = 1 % p;
	while (b)
	{
		if (b & 1) res = res * a % p;
		b >>= 1;
		a = a * a % p;
	}
	return res;
}

void init_f()
{
	f[0] = uf[0] = 1;
    for (int i = 1; i < N; i ++ )
        f[i] = f[i - 1] * i % P;
    uf[N - 1] = qpow(f[N - 1], P - 2, P);
    for (int i = N - 2; i > 0; i -- )
    	uf[i] = uf[i + 1] * (i + 1) % P;
}

int A(int x, int y)
{
    if (x < y) return 0;
	return f[x] * uf[x - y] % P;
}

main()
{
	scanf("%lld%lld", &T, &P);
	
	init_f();
	
	if (is_prime(P))
	{
		while (T -- )
		{
			scanf("%lld%lld", &n, &m);
			printf("%lld\n", A(n - m + 1, m));
		}
	}
	else
	{
		while (T -- )
		{
			int res = 1;
			scanf("%lld%lld", &n, &m);
			for (int i = n - m + 1; i > n - 2 * m + 1; i -- )
				res = res * i % P;
			printf("%lld\n", res);
		}
	}
	
	return 0;
}

e. Lucas(Extra)

如果数据范围更大呢？

1 ≤ n , m ≤ 1 0 18 1 ≤ n, m ≤ 10^{18} 1≤n,m≤1018，P 为质数且 1 0 4 ≤ P ≤ 1 0 5 10^4 ≤ P ≤ 10^5 104≤P≤105。

注意模数很小且为质数，可以考虑 Lucas \text{Lucas} Lucas 定理，这样能将值域缩小为 P P P，可以使用做法 d d d。

时间复杂度： O ( P + max ⁡ log ⁡ P m ) O(P + \max \log_P m) O(P+maxlogP​m)。

f. CRT(Extra)

还可以再加强吗？

1 ≤ n , m ≤ 1 0 18 ， 1 0 17 ≤ P ≤ 1 0 18 1 ≤ n, m ≤ 10^{18}，10^{17} ≤ P ≤ 10^{18} 1≤n,m≤1018，1017≤P≤1018， P P P 不含平方质因子， P P P 中最大的质因子不超过 1 0 5 10^5 105。

模数甚至可以不是质数！考虑将模数质因数分解。

那么，分解的结果应为若干个 P P P’，每个都为质数。

则可以使用做法 e e e 对这些 P P P′ 分别求解，最后利用 CRT \text{CRT} CRT 合并答案。

C T351142 只因字塔的探索

3.1 涉及知识点

动态规划、区间DP、记忆化搜索

3.2 解题思路

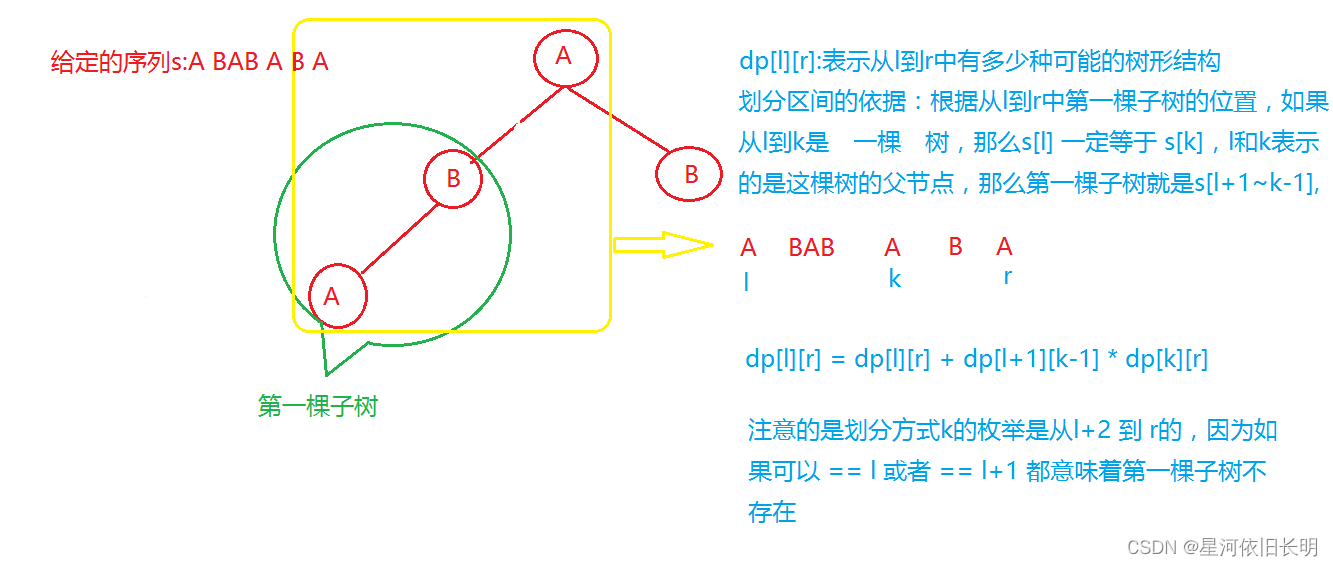
a. 区间DP（100pts）

#include <cstring>
#include <iostream>
#include <algorithm>
#include <string.h>

using namespace std;

typedef long long LL;

const int N = 310, mod = 1e9;

char str[N];
int f[N][N];

int main()
{
    cin >> str + 1;
    int n = strlen(str + 1);
    if (n % 2 == 0) cout << 0 << endl;
    else
    {
        for (int len = 1; len <= n; len += 2)
            for (int l = 1; l + len - 1 <= n; l ++ )
            {
                int r = l + len - 1;
                if (len == 1) f[l][r] = 1;
                else if (str[l] == str[r])
                {
                    for (int k = l; k < r; k += 2)
                        if (str[k] == str[r])
                            f[l][r] = (f[l][r] + (LL)f[l][k] * f[k + 1][r - 1]) % mod;
                }
            }

        cout << f[1][n] << endl;
    }

    return 0;
}

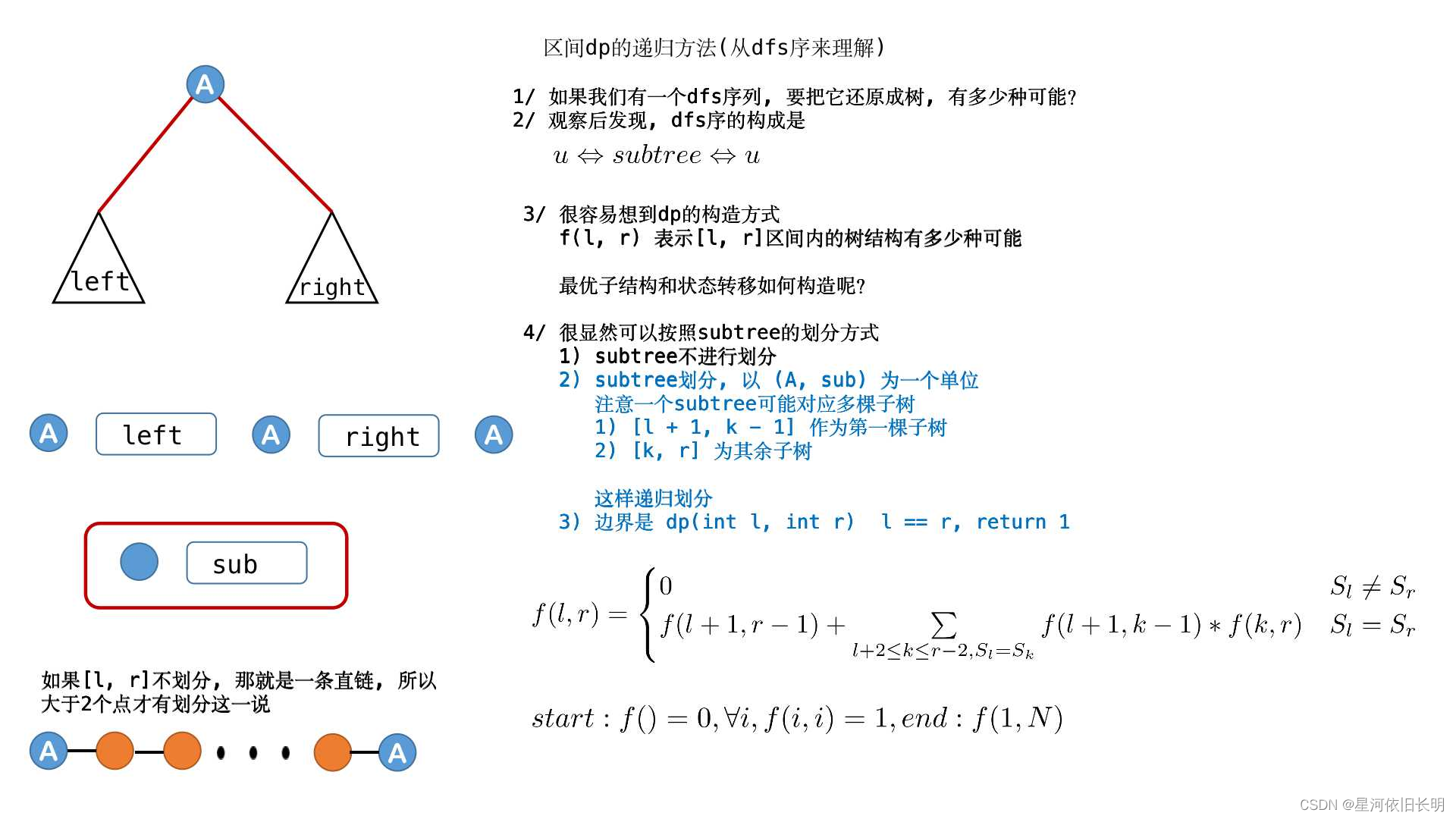
b. 记忆化搜索（100pts）

#include <iostream>
#include <cstring>

using namespace std;

typedef long long LL;

const int N = 310, mod = 1e9;

int n;
char str[N];
int f[N][N];

int dp(int l, int r)
{
	if (l > r) return 0;
	if (l == r) return 1;
	int& ans = f[l][r];
	if (ans != -1) return ans;

	ans = 0;
	if (str[l] == str[r])
		for (int k = l + 2; k <= r; k ++ )
			ans = (ans + (LL)dp(l + 1, k - 1) * (LL)dp(k, r)) % mod;

	return ans;
}

int main()
{
	scanf("%s", str + 1);
	n = strlen(str + 1);

	memset(f, -1, sizeof f);
	printf("%d\n", dp(1, n));
	
	return 0;
}

D T352449 三体世界的毁灭

4.1 题意简述

在一个二维平面上给定 n n n 个点，请你画出一个最小的能够包含所有点的圆。

4.2 涉及知识点

计算几何、最小圆覆盖

4.3 解题思路（100pts）



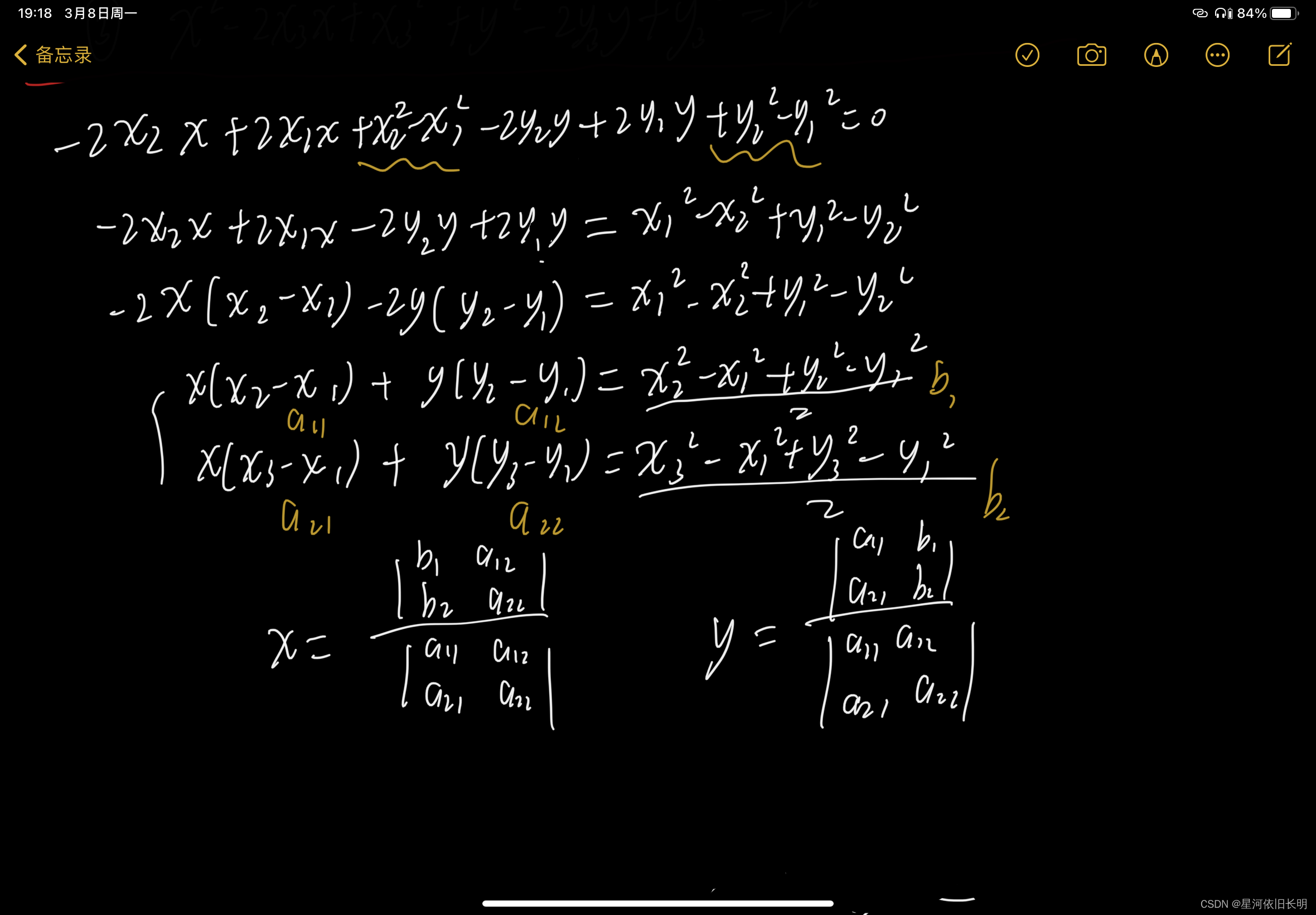
经过化简类别，就能得到③ - ①的式子（大括号第二个）

根据行列式解二元一次方程组的性质，我们就能确定这个圆的圆心的坐标是多少了（不会也可以解，只不过可以直接套行列式）

从第一个点开始作为初始圆，圆心就是这个点 ( a 1 a_1 a1​)，然后依次向后枚举( a i a_i ai​)，如果下一个点在当前已知的圆的内部，我们就继续枚举下一个点；而如果此时这个点在当前圆的外部，我们就要重新设置一个新的圆了

枚举 i i i 前面的点 j j j，如果此时两个点以他们的连线的中点作为圆心，两点连线作为直径，继续枚举j前面的点 k k k，如果此时 k k k 在此时的圆外，那么 i ， j ， k i，j，k i，j，k 三个点组成的圆就是目前的最优解。

简易证明：我们取点1，点2，点4进行三点定圆. 因为第四个点不在前三个点的圆中.所以第四个点定的新圆一定比前三个定的圆大.

注：这里第一行无论输出什么，后面的半径和坐标都需要输出。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>

#define x first
#define y second

using namespace std;

typedef pair<double, double> PDD;
const int N = 100010;
const double eps = 1e-12;
const double PI = acos(-1);

int n;
PDD q[N];
struct Circle
{
    PDD p;
    double r;
};

int sign(double x)
{
    if (fabs(x) < eps) return 0;
    if (x < 0) return -1;
    return 1;
}

int dcmp(double x, double y)
{
    if (fabs(x - y) < eps) return 0;
    if (x < y) return -1;
    return 1;
}

PDD operator- (PDD a, PDD b)
{
    return {a.x - b.x, a.y - b.y};
}

PDD operator+ (PDD a, PDD b)
{
    return {a.x + b.x, a.y + b.y};
}

PDD operator* (PDD a, double t)
{
    return {a.x * t, a.y * t};
}

PDD operator/ (PDD a, double t)
{
    return {a.x / t, a.y / t};
}

double operator* (PDD a, PDD b)
{
    return a.x * b.y - a.y * b.x;
}

PDD rotate(PDD a, double b)
{
    return {a.x * cos(b) + a.y * sin(b), -a.x * sin(b) + a.y * cos(b)};
}

double get_dist(PDD a, PDD b)
{
    double dx = a.x - b.x;
    double dy = a.y - b.y;
    return sqrt(dx * dx + dy * dy);
}

PDD get_line_intersection(PDD p, PDD v, PDD q, PDD w)
{
    auto u = p - q;
    double t = w * u / (v * w);
    return p + v * t;
}

pair<PDD, PDD> get_line(PDD a, PDD b)
{
    return {(a + b) / 2, rotate(b - a, PI / 2)};
}

Circle get_circle(PDD a, PDD b, PDD c)
{
    auto u = get_line(a, b), v = get_line(a, c);
    auto p = get_line_intersection(u.x, u.y, v.x, v.y);
    return {p, get_dist(p, a)};
}

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%lf%lf", &q[i].x, &q[i].y);
    random_shuffle(q, q + n);

    Circle c({q[0], 0});
    for (int i = 1; i < n; i ++ )
        if (dcmp(c.r, get_dist(c.p, q[i])) < 0)
        {
            c = {q[i], 0};
            for (int j = 0; j < i; j ++ )
                if (dcmp(c.r, get_dist(c.p, q[j])) < 0)
                {
                    c = {(q[i] + q[j]) / 2, get_dist(q[i], q[j]) / 2};
                    for (int k = 0; k < j; k ++ )
                        if (dcmp(c.r, get_dist(c.p, q[k])) < 0)
                            c = get_circle(q[i], q[j], q[k]);
                }
        }

	if (c.r > 10000) puts("No");
	else puts("Yes");
	printf("%.6lf %.6lf\n%.6lf\n", c.p.x, c.p.y, c.r);
	
    return 0;
}

最后，如果觉得对您有帮助的话，点个赞再走吧！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/756374.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

CRC算法并行运算Verilog实现

CRC算法并行运算Verilog实现

因为CRC循环冗余校验码的算法和硬件电路结构比较简单&#xff0c;所以CRC是一种在工程中常用的数据校验方法。尽管CRC简单&#xff0c;但在工程应用中还是有些问题会对工程师产生困惑。这篇文章将介绍一下CRC&#xff0c;希望对大家有所帮助。 一、CRC算法介绍 CRC校验原理看起…
阅读更多...
PPO(Proximal Policy Optimization Algorithms)论文解读及实现

PPO(Proximal Policy Optimization Algorithms)论文解读及实现

论文标题&#xff1a;Proximal Policy Optimization Algorithms 核心思路&#xff1a;使用off policy 代替on policy,用一个策略网络来产生数据&#xff0c;用一个策略网络来更新参数&#xff0c;分别为policy_old和policy 0 摘要 Whereas standard policy gradient methods …
阅读更多...
Python自动化办公：pptx篇

Python自动化办公：pptx篇

文章目录 简介能做什么PPT要素介绍官方demo高阶引申参考文献 202201笔记迁移 简介 python-pptx包是用来自动化处理ppt的。 使用的第一步是安装 pip install python-pptx相比python-docx&#xff0c;python-pptx的使用更为麻烦一些&#xff0c;原因有很多&#xff0c;比如说&…
阅读更多...
波奇学Linux:make和Makefile

波奇学Linux:make和Makefile

make和Makefile自动化构建并能决定源文件调用顺序&#xff0c;同时不必再写gcc命令 第一行依赖关系&#xff0c;第二行是tab键开头&#xff0c;是依赖方法 依赖关系&#xff1a;目标文件&#xff1a;依赖文件。 依赖方法&#xff1a;目标文件和依赖文件间的关系。 如果只有一条…
阅读更多...
es下载历史的tar文件

es下载历史的tar文件

第一步进入官网找到历史版本 第二步复制历史版本名称组合成下面的链接 直接get访问下载。如下链接所示只需要修改7.3.0这个版本号 https://artifacts.elastic.co/downloads/elasticsearch/elasticsearch-7.3.0-linux-x86_64.tar.gz
阅读更多...
ChatGLM使用记录

ChatGLM使用记录

ChatGLM ChatGLM-6B 是一个开源的、支持中英双语的对话语言模型&#xff0c;基于 General Language Model (GLM) 架构&#xff0c;具有 62 亿参数。结合模型量化技术&#xff0c;用户可以在消费级的显卡上进行本地部署&#xff08;INT4 量化级别下最低只需 6GB 显存&#xff0…
阅读更多...
opencv实战--角度测量和二维码条形码识别

opencv实战--角度测量和二维码条形码识别

文章目录 前言一、鼠标点击的角度测量二、二维码条形码识别 前言 一、鼠标点击的角度测量 首先导入一个带有角度的照片 然后下面的代码注册了一个鼠标按下的回调函数&#xff0c; 还有一个点的数列&#xff0c;鼠标事件为按下的时候就记录点&#xff0c;并画出点&#xff0c;…
阅读更多...
uniapp微信小程序上传体积压缩包过大分包操作和上传时遇到代码质量未通过问题

uniapp微信小程序上传体积压缩包过大分包操作和上传时遇到代码质量未通过问题

1&#xff1a;首先我们得从项目最初阶段就得考虑项目是否要进行分包操作&#xff0c;如果得分包&#xff0c;我们应该创建一个与pages同级的文件夹&#xff0c;命名可以随意 2:第二部我们将需要分包的文件和页面放到分包文件夹里面subpage&#xff0c;这里我们得注意&#xff…
阅读更多...
Python基础语法第三章之顺序循环条件

Python基础语法第三章之顺序循环条件

目录 一、顺序语句 二、条件语句 2.1什么是条件语句 2.2语法格式 2.2.1 if 2.2.2if - else 2.2.3if - elif - else 2.3缩进和代码块 2.4闰年的判断练习 2.5空语句 pass 三、循环语句 3.1while 循环 3.1.1代码示例练习 3.2 for 循环 ​3.3 continue 3.4 break 一…
阅读更多...
给LLM装上知识：从LLM+LangChain的本地知识库问答到LLM与知识图谱的结合

给LLM装上知识：从LLM+LangChain的本地知识库问答到LLM与知识图谱的结合

前言 过去半年&#xff0c;随着ChatGPT的火爆&#xff0c;直接带火了整个LLM这个方向&#xff0c;然LLM毕竟更多是基于过去的经验数据预训练而来&#xff0c;没法获取最新的知识&#xff0c;以及各企业私有的知识 为了获取最新的知识&#xff0c;ChatGPT plus版集成了bing搜…
阅读更多...
linux常用工具介绍

linux常用工具介绍

文章目录 前言目录文件查看ls1、查看详细信息&#xff08;文件大小用K、M等显示&#xff09;2、按照文件创建时间排序&#xff08;常在查看日志时使用&#xff09; sort1、排序数字 df 、du1、查看目录的大小2、查看目录 从大到小排序 显示前n个3、查看磁盘使用情况 tailf一些目…
阅读更多...
银河麒麟高级服务器操作系统V10安装mysql数据库

银河麒麟高级服务器操作系统V10安装mysql数据库

一、安装前 1.检查是否已经安装mysql rpm -qa | grep mysql2.将查询出的包卸载掉 rpm -e --nodeps 文件名3.将/usr/lib64/libLLVM-7.so删除 rm -rf /usr/lib64/libLLVM-7.so4.检查删除结果 rpm -qa | grep mysql5.搜索残余文件 whereis mysql6.删除残余文件 rm -rf /usr/b…
阅读更多...
怎么用二维码做企业介绍？企业宣传二维码2种制作方法

怎么用二维码做企业介绍？企业宣传二维码2种制作方法

怎么做一个企业推广二维码呢&#xff1f;现在制作二维码来做宣传推广是常用的一种方式&#xff0c;一般需要包含企业介绍、工作环境、产品简介、宣传视频、公司地址等等方面内容&#xff0c;那么企业介绍二维码该如何制作&#xff1f;下面给大家分享一下使用二维码编辑器&#…
阅读更多...
EventBus详解

EventBus详解

目录 1 EventBus 简介简介角色关系图四种线程模型 2.EventBus使用步骤添加依赖注册解注册创建消息类发送消息接收消息粘性事件发送消息 使用postStick()接受消息 3 EventBus做通信优点4 源码getDefault()register()findSubscriberMethods方法findUsingReflection方法findUsingR…
阅读更多...
前端部署项目，经常会出现下载完 node 或者 npm 运行时候发现，提示找不到

前端部署项目，经常会出现下载完 node 或者 npm 运行时候发现，提示找不到

1. 首先要在下载时候选择要下载的路径&#xff0c;不能下载完后&#xff0c;再拖拽到其他文件夹&#xff0c;那样就会因为下载路径和当前路径不一致&#xff0c;导致找不到相关变量。 2. 所以一开始就要在下载时候确定要存放的路径&#xff0c;然后如果运行报错&#xff0c;就…
阅读更多...
【Java基础教程】（十三）面向对象篇 · 第七讲：继承性详解——继承概念及其限制，方法覆写和属性覆盖，关键字super的魔力~

【Java基础教程】（十三）面向对象篇 · 第七讲：继承性详解——继承概念及其限制，方法覆写和属性覆盖，关键字super的魔力~

Java基础教程之面向对象 第七讲 本节学习目标1️⃣ 继承性1.1 继承的限制 2️⃣ 覆写2.1 方法的覆写2.2 属性的覆盖2.3 关键字 this与 super的区别 3️⃣ 继承案例3.1 开发数组的父类3.2 开发排序类3.3 开发反转类 &#x1f33e; 总结 本节学习目标 掌握继承性的主要作用、实…
阅读更多...
git指令记录

git指令记录

参考博客&#xff08;侵权删&#xff09;&#xff1a;关于Git这一篇就够了_17岁boy想当攻城狮的博客-CSDN博客 Git工作区介绍_git 工作区_xyzso1z的博客-CSDN博客 git commit 命令详解_gitcommit_辰风沐阳的博客-CSDN博客 本博客只作为自己的学习记录&#xff0c;无商业用途&…
阅读更多...
计算机存储设备

计算机存储设备

缓存为啥比内存快 内存使用 DRAM 来存储数据的、也就是动态随机存储器。内部使用 MOS 和一个电容来存储。 需要不停地给它刷新、保持它的状态、要是不刷新、数据就丢掉了、所以叫动态 、DRAM 缓存使用 SRAM 来存储数据、使用多个晶体管(比如6个)就是为了存储1比特 内存编码…
阅读更多...
【python】python全国数据人均消费数据分析（代码+报告+数据）【独一无二】

【python】python全国数据人均消费数据分析（代码+报告+数据）【独一无二】

&#x1f449;博__主&#x1f448;&#xff1a;米码收割机 &#x1f449;技__能&#x1f448;&#xff1a;C/Python语言 &#x1f449;公众号&#x1f448;&#xff1a;测试开发自动化 &#x1f449;荣__誉&#x1f448;&#xff1a;阿里云博客专家博主、51CTO技术博主 &#x…
阅读更多...
bio、nio、aio、io多路复用

bio、nio、aio、io多路复用

BIO-同步阻塞IO NIO-同步非阻塞IO 不断的重复发起IO系统调用&#xff0c;这种不断的轮询&#xff0c;将会不断地询问内核&#xff0c;这将占用大量的 CPU 时间&#xff0c;系统资源利用率较低 IO多路复用模型-异步阻塞IO IO多路复用模型&#xff0c;就是通过一种新的系统调用&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023