论文标题：Proximal Policy Optimization Algorithms
核心思路：使用off policy 代替on policy,用一个策略网络来产生数据，用一个策略网络来更新参数，分别为policy_old和policy

0 摘要

• Whereas standard policy gradient methods perform one gradient update per data sample, we propose a novel objective function that enables multiple epochs of minibatch updates
  由于标准的策略梯度算法每轮数据（每轮数据定义：从游戏开始到结束的一轮完整数据）只能更新一个梯度，提出了一种新的方法，使得每个数据集上可以更新多次。
• The new methods, which we call proximal policy optimization (PPO), have some of the benefits of trust region policy optimization (TRPO),
• 新提出的方法命名为 PPO,一些启发受益于TRPO。

1 Introduction

We propose a novel objective with clipped probability ratios, which forms a pessimistic estimate (i.e., lower bound) of the performance of the policy. To optimize policies, we alternate between sampling data from the policy and performing several epochs of optimization on the sampled data.
我们提出了一个新的目标（使概率clip在一个区间内），形成一个悲观的估计 (即，数据下界)。为了优化策略，我们在从策略中采样数据和对采样数据执行若干次优化之间交替进行。

2 Background: Policy Optimization

2.1 Policy Gradient Methods

$$\hat{g}={\hat{E}}_t[{\nabla }_{\theta }log{\pi }_{\theta }(a_t|s_t){\hat{A}}_t]$$

where π theta is a stochastic policy and Aˆt is an estimator of the advantage function at timestep t.

$$L^{PG}(\theta )={\hat{E}}_t[log{\pi }_{\theta }(a_t|s_t){\hat{A}}_t]$$

3 Clipped Surrogate Objective

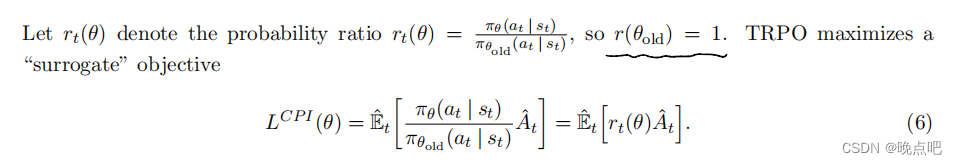
Without a constraint, maximization of LCPI would lead to an excessively large policy update; hence, we now consider how to modify the objective, to penalize changes to the policy that move rt(θ) away from 1.
如果对（6）式没有约束，这个值将会导致过大的策略更新，我们现在考虑修改这个目标，惩罚远离1的策略变化
The main objective we propose is the following:
我们提出的目标函数如下：

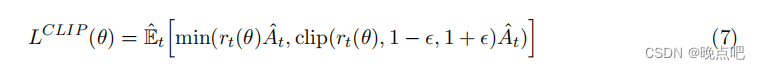
通过公式（7）,我们clip后的值取的是clip之前值的下界。
其中奖励At可能是整数，也可能是负数。

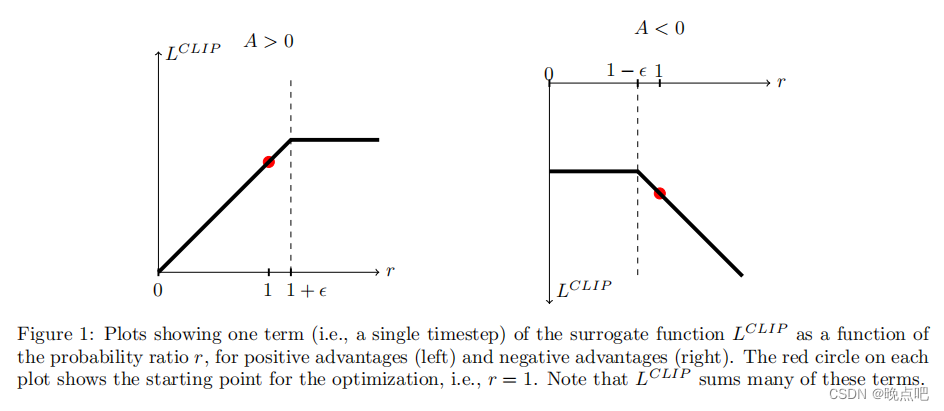
plots a single term (i.e., a single t) in LCLIP ; note that the probability ratio r is clipped at 1 − epsilon 到1+epsilon ，depending on whether the advantage is positive or negative.

4 Adaptive KL Penalty Coefficient

In our experiments, we found that the KL penalty performed worse than the clipped surrogate objective, however, we’ve included it here because it’s an important baseline.
在我们的实验中，发现实验KL散度惩罚项，没有CLIP效果好，这里仅作为一个baseline。

5 Algorithm

If using a neural network architecture that shares parameters between the policy and value function, we must use a loss function that combines the policy surrogate and a value function error term. This objective can further be augmented by adding an entropy bonus to ensure sufficient exploration.
Combining these terms, we obtain the following objective, which is (approximately) maximized each iteration:
如果使用一个神经网络架构在策略这价值函数共享参数，我们必须使用一个结合策略代理和价值函数误差项。这个目标可以被参数为添加熵奖励以确保足够的探索,
结合这些项，我们可以得到以下目标函数，最大化每一步迭代。

each of N (parallel) actors collect T timesteps of data. Then we construct the surrogate loss on these NT timesteps of data, and optimize it with minibatch SGD (or usually for better performance, Adam [KB14]), for K epochs.
共用大N个Actor,每个Actor收集T步的数据，然后构建surrogate 损失在这N*T的数据集上，我们使用小批量SGD来优化这个损失函数。-=

6 算法实现（pytorch）

以LunarLander-v2（月球着陆）游戏为例：
环境基本属性：
状态维度：state_dim=8
动作空间：action_dim=4

6.1 memory

用于存储游戏过程中的游戏数据，包含以下参数：
游戏每步选择的动作：actions=[]
游戏每步的状态：states=[]
每步动作出现的概率：logprobs=[]
每步动作的奖励：rewards=[]
是否游戏结束了：is_terminals=[]
通过以下代码获取actions,states,logprobs,
注意：memory 是policy_old 网络生成的
再通过环境执行action后，可以得到reward和is_terminal。
（完整代码见最后部分）

        state = torch.from_numpy(state).float().to(device)  	# 输入当前状态
        action_probs = self.action_layer(state)   # 经过action 网络层，输出动作概率
        dist = Categorical(action_probs)#按照给定的概率分布来进行采样
        action = dist.sample() # 安装aciton 概率，采样出一个action
        memory.states.append(state) # 添加当前状态
        memory.actions.append(action) # 添加当前动作
        memory.logprobs.append(dist.log_prob(action)) # 添加当前 概率

6.2 policy 网络结构

action 网络结构如下，输入为状态维度8，输出为action维度4。即输入环境状态，输出选择的aciton概率。
input_dim (batch_size,8)
output_dim (batch_size,4)
网络结构如下：

 # actor
self.action_layer = nn.Sequential(
                nn.Linear(state_dim, n_latent_var),
                nn.Tanh(),
                nn.Linear(n_latent_var, n_latent_var),
                nn.Tanh(),
                nn.Linear(n_latent_var, action_dim),
                nn.Softmax(dim=-1)
                )

critic网络输入为环境状态，维度为8，输出维度为1。即一个值，用于对当前状态的评价得分。
input_dim (batch_size,8)
output_dim (batch_size,1)
网络结构如下：

# critic
self.value_layer = nn.Sequential(
              nn.Linear(state_dim, n_latent_var),
              nn.Tanh(),
              nn.Linear(n_latent_var, n_latent_var),
              nn.Tanh(),
              nn.Linear(n_latent_var, 1)
              )
      

6.3 模型更新

上面memory存储游戏一定步数后，数据既可以开始用于网络训练。

• 当前步reward 计算
  后续步reward对当前步reward是逐步衰减的。
  

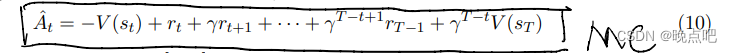
        rewards = []
        discounted_reward = 0
        # 使用reversed将奖励翻转，从最后一步往前计算累计衰减奖励。
        for reward, is_terminal in zip(reversed(memory.rewards), reversed(memory.is_terminals)):
            if is_terminal:
                discounted_reward = 0
            discounted_reward = reward + (self.gamma * discounted_reward)
            rewards.insert(0, discounted_reward)

使用新policy网络，输入old_states, old_actions，可以得到，新的action概率分布，和critical 值。

 logprobs, state_values, dist_entropy = self.policy.evaluate(old_states, old_actions)

• 论文核心公式实现
  

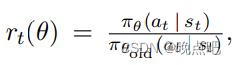
# Finding the ratio (pi_theta / pi_theta__old):
 ratios = torch.exp(logprobs - old_logprobs.detach())

公式中A_t: advantages = rewards - state_values.detach()

# Finding Surrogate Loss:
 advantages = rewards - state_values.detach()

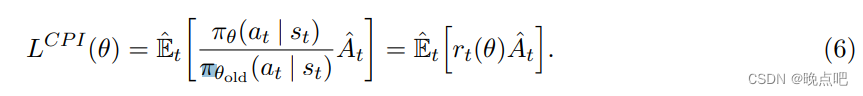
surr1 = ratios * advantages

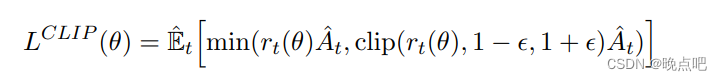
surr2 = torch.clamp(ratios, 1-self.eps_clip, 1+self.eps_clip) * advantages
 -torch.min(surr1, surr2)

损失函数公式：

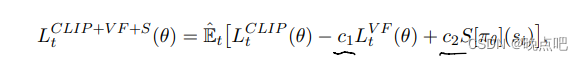
loss = -torch.min(surr1, surr2) + 0.5*self.MseLoss(state_values, rewards) - 0.01*dist_entropy

新的policy网络更新K次后，将新的模型参数复制给老网络。然后使用老网络产生新的训练数据，再使用新的训练数据更新新的网络，如此往复循环。