因为CRC循环冗余校验码的算法和硬件电路结构比较简单，所以CRC是一种在工程中常用的数据校验方法。尽管CRC简单，但在工程应用中还是有些问题会对工程师产生困惑。这篇文章将介绍一下CRC，希望对大家有所帮助。

一、CRC算法介绍

        CRC校验原理看起来比较复杂，好难懂，因为大多数书上基本上是以二进制的多项式形式来说明的。其实很简单的问题，其根本思想就是先在要发送的帧后面附加一个数（这个就是用来校验的校验码，但要注意，这里的数也是二进制序列的，下同），生成一个新帧发送给接收端。当然，这个附加的数不是随意的，它要使所生成的新帧能与发送端和接收端共同选定的某个特定数整除（注意，这里不是直接采用二进制除法，而是采用一种称之为“模2除法”）。到达接收端后，再把接收到的新帧除以（同样采用“模2除法”）这个选定的除数。因为在发送端发送数据帧之前就已通过附加一个数，做了“去余”处理（也就已经能整除了），所以结果应该是没有余数。如果有余数，则表明该帧在传输过程中出现了差错。

     【说明】“模2除法”与“算术除法”类似，但它既不向上位借位，也不比较除数和被除数的相同位数值的大小，只要以相同位数进行相除即可。模2加法运算为：1+1=0，0+1=1，0+0=0，无进位，也无借位；模2减法运算为：1-1=0，0-1=1，1-0=1，0-0=0，也无进位，无借位。相当于二进制中的逻辑异或运算。也就是比较后，两者对应位相同则结果为“0”，不同则结果为“1”。如100101除以1110，结果得到商为11，余数为1，如左图所示。如11×11=101，如右图所示。

         具体来说，CRC校验原理就是以下几个步骤：

        （1）先选择（可以随机选择，也可按标准选择，具体在后面介绍）一个用于在接收端进行校验时，对接收的帧进行除法运算的除数（是二进制比较特串，通常是以多项方式表示，所以CRC又称多项式编码方法，这个多项式也称之为“生成多项式”）。

        （2）看所选定的除数二进制位数（假设为k位），然后在要发送的数据帧（假设为m位）后面加上k-1位“0”，然后以这个加了k-1个“0“的新帧（一共是m+k-1位）以“模2除法”方式除以上面这个除数，所得到的余数（也是二进制的比特串）就是该帧的CRC校验码，也称之为FCS（帧校验序列）。但要注意的是，余数的位数一定要是比除数位数只能少一位，哪怕前面位是0，甚至是全为0（附带好整除时）也都不能省略。

        （3）再把这个校验码附加在原数据帧（就是m位的帧，注意不是在后面形成的m+k-1位的帧）后面，构建一个新帧发送到接收端；最后在接收端再把这个新帧以“模2除法”方式除以前面选择的除数，如果没有余数，则表明该帧在传输过程中没出错，否则出现了差错。

        通过以上介绍，大家一定可以理解CRC校验的原理，并且不再认为很复杂吧。

        从上面可以看出，CRC校验中有两个关键点：一是要预先确定一个发送端和接收端都用来作为除数的二进制比特串（或多项式）；二是把原始帧与上面选定的除进行二进制除法运算，计算出FCS。前者可以随机选择，也可按国际上通行的标准选择，但最高位和最低位必须均为“1”，如在IBM的SDLC（同步数据链路控制）规程中使用的CRC-16（也就是这个除数一共是17位）生成多项式g（x）= x16 + x15 + x2 +1（对应二进制比特串为：11000000000000101）；而在ISO HDLC（高级数据链路控制）规程、ITU的SDLC、X.25、V.34、V.41、V.42等中使用CCITT-16生成多项式g（x）= x16 + x15 + x5 +1（对应二进制比特串为：11000000000100001）。

        由以上分析可知，既然除数是随机，或者按标准选定的，所以CRC校验的关键是如何求出余数，也就是校验码（CRC校验码）。

    下面以一个例子来具体说明整个过程。现假设选择的CRC生成多项式为G（X） = X4 + X3 + 1，要求出二进制序列10110011的CRC校验码。下面是具体的计算过程：

         （1）首先把生成多项式转换成二进制数，由G（X） = X4 + X3 + 1可以知道（，它一共是5位（总位数等于最高位的幂次加1，即4+1=5），然后根据多项式各项的含义（多项式只列出二进制值为1的位，也就是这个二进制的第4位、第3位、第0位的二进制均为1，其它位均为0）很快就可得到它的二进制比特串为11001。

        （2）因为生成多项式的位数为5，根据前面的介绍，得知CRC校验码的位数为4（校验码的位数比生成多项式的位数少1）。因为原数据帧10110011，在它后面再加4个0，得到101100110000，然后把这个数以“模2除法”方式除以生成多项式，得到的余数（即CRC码）为0100，如图5-10所示。注意参考前面介绍的“模2除法”运算法则。

       

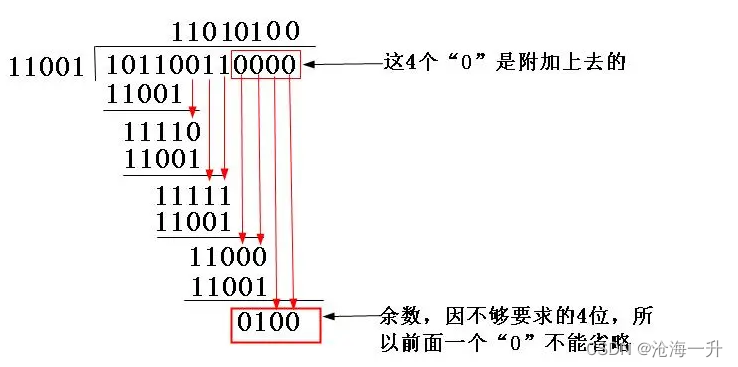
         （3）把上步计算得到的CRC校验0100替换原始帧101100110000后面的四个“0”，得到新帧101100110100。再把这个新帧发送到接收端。

        （4）当以上新帧到达接收端后，接收端会把这个新帧再用上面选定的除数11001以“模2除法”方式去除，验证余数是否为0，如果为0，则证明该帧数据在传输过程中没有出现差错，否则出现了差错。

    通过以上CRC校验原理的剖析和CRC校验码的计算示例的介绍，大家应该对这种看似很复杂的CRC校验原理和计算方法应该比较清楚了。 

二、CRC算法并行实现

1、实现流程

        （1） 用N表示数据宽度，M表示CRC宽度。例如，如果我们想为4位数据路径生成并行USB CRC5，N=4，M=5。

        （2） 使用给定的多项式或十六进制表示法实现串行CRC生成器例程。

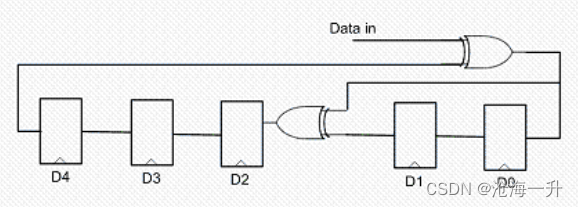
         （3） 并行CRC实现是N位数据输入和M位当前状态CRC的函数，如下图所示。我们将构建两个矩阵：当N=0时，作为Min（当前状态CRC）函数的Mout（下一状态CRC）和当M=0时，作为Nin的函数的Mout。

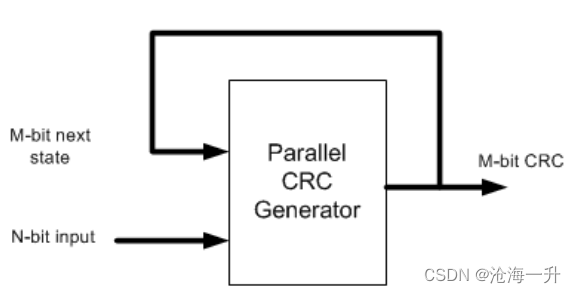
         （4） 当Min＝0时，使用（2）中的例程计算N个值的CRC。每个值都是one-hot的，也就是说只有一个位为1。对于N=4，值为0x1、0x2、0x4、0x8。Mout=F（Nin，Min=0）

        （5） 构建NxM矩阵，每一行包含按递增顺序来自（3）的结果。例如，第1行包含输入=0x1的结果，第2行为输入=0x2等。输出为M位宽，即所需的CRC宽度。以下是N=4的USB CRC5的矩阵。

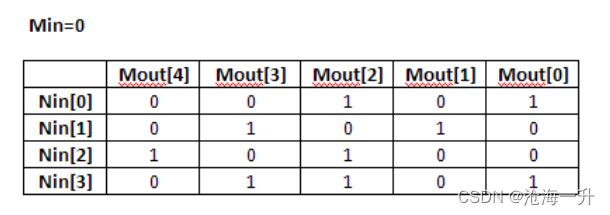
         （6） 这个矩阵中的每一列，表示输出位Mout[i]作为Nin的函数。

        （7） 当Nin＝0时，使用（3）中的例程计算M个值的CRC。每个值都是一个one-hot的，也就是说只有一个位为1。对于M=5，值为0x1、0x2、0x4、0x8、0x10。Mout=F（Nin=0，最小值）

        （8） 构建MxM矩阵，每一行包含按递增顺序来自（7）的结果。以下是N=4的USB CRC5的矩阵：

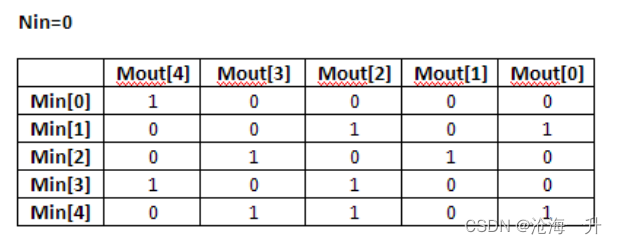
         （9） 现在，为每个Mout[i]位建立一个等式：列[i]中的所有Nin[j]和Min[k]位都参与该等式。参与的输入被异或在一起。

        Mout[0] = Min[1]^Min[4]^Nin[0]^Nin[3]

        Mout[1] = Min[2]^Nin[1]

        Mout[2] = Min[1]^Min[3]^Min[4]^Nin[0]^Nin[2]^Nin[3]

        Mout[3] = Min[2]^Min[4]^Nin[1]^Nin[3]

        Mout[4] = Min[0]^Min[3]^Nin[2]

        这就是并行CRC的输出。

2、实例及代码

        我们以CRC8举例，多项式G(x)=X8 +X7 +X6 +X4 +X2 +1 ，则其串行CRC代码如下：

//G(x)=X^8 +X^7 +X^6 +X^4 +X^2 + X^0
//input bit number = 1
// 
module CRC8_1BIT(
DATA,
CRC_OUT,
RESET,
ENABLE,
CLK);
input DATA;
input RESET;
input ENABLE;
input CLK;
output [7:0] CRC_OUT;
wire DATA
wire RESET;
wire ENABLE
wire CLK
reg [7:0] CRC_OUT;

wire LFSR_N
reg [7:0] LFSR_S;

assign LFSR_N=CRC_OUT[7]^DATA;

always@(*) begin
    LFSR_S[0] = LFSR_S[7] ;
    LFSR_S[1] = LFSR_S[0] ;
    LFSR_S[2] = LFSR_S[1]^LFSR_N ;
    LFSR_S[3] = LFSR_S[2] ;
    LFSR_S[4] = LFSR_S[3]^LFSR_N ;
    LFSR_S[5] = LFSR_S[4] ;
    LFSR_S[6] = LFSR_S[5]^LFSR_N ;
    LFSR_S[7] = LFSR_S[6]^LFSR_N ;
end

always@ (posedge CLK or posedge RESET) begin
    if(RESET) begin
        CRC_OUT <= 8’ hff;
    else if (ENABLE) begin
        CRC_OUT <= LFSR_S;
    end
end

endnodule

        然后根据这个LFSR迭代得到矩阵：

module crc8_paralle( 
input [7:0] data_in, 
output reg[7:0] crc8, 
input rst,
input cik
);
// LFSR for crc8 
function [7:0] crc8_serial; 
input [7:0] crc;
input data; 
begin 
    crc8_serial[0] = data^crc[7] ;
    crc8_serial[1] = crc[0] ;
    crc8_serial[2] = data^crc[7]^crc[1] ;
    crc8_serial[3] = crc[2] ;
    crc8_serial[4] = data^crc[7]^crc[3] ;
    crc8_serial[5] = crc[4] ;
    crc8_serial[6] = data^crc[7]^crc[5] ;
    crc8_serial[7] = data^crc[7]^crc[6] ;
end
endfunction

// 8 iterations of crc8 LFSR 
function [7:0] crc_iteration 
input [7:0] crc;
input [7:0] data integer i;
begin
crc_iteration = crc; 
for( i=0 ; i<8 ; i=i+1)
    crc_iteration = crc8_serial(crc_iteration, data[7-i]); 
end
endfunction

always@( posedge clk or posedge rst) begin 
    if(rst) begin
        crc8 <= 8'hff; 
    end
    else begin
        crc8 <= crc_iteration(crc8,data_in) ;
    end
end

endmodule

        输入data_in 的是8‘b00000001，得到crc8的值，就是H1的第一行8’hd5；输入data_in 的是8‘b00000010，得到crc8的值，就是H1的第二行8’h7f；以此类推。计算出上面矩阵H1=[]NxM。计算H2=[]MxM的方法和H1是一样的。经过上面计算得到矩阵：

// G (x) = X^8 +X^7 +X^6 +X^4 +X^2 +X^0
//input bit number 8
Nin[O]  1  1  0  1  0  1  0  1  
Nin[1]  0  1  1  1  1  1  1  1
Nin[2]  1  1  1  1  1  1  1  0
Nin[3]  0  0  1  0  1  0  0  1   H1
Nin[4]  0  1  0  1  0  0  1  0
Nin[5]  1  0  1  0  0  1  0  0
Nin[6]  1  0  0  1  1  1  0  1
Nin[7]  1  1  1  0  1  1  1  1
----------------------------------
Min[O]  1  1  0  1  0  1  0  1  
Min[1]  0  1  1  1  1  1  1  1
Min[2]  1  1  1  1  1  1  1  0
Min[3]  0  0  1  0  1  0  0  1   H2
Min[4]  0  1  0  1  0  0  1  0
Min[5]  1  0  1  0  0  1  0  0
Min[6]  1  0  0  1  1  1  0  1
Min[7]  1  1  1  0  1  1  1  1
----------------------------------
nxt_crc 7  6  5  4  3  2  1  0

           此时，我们可以写出并行CRC的Verilog程序：

//G(x)=X^8 +X^7 +X^6 +X^4 +X^2 + X^0
//input bit number = 1 
module CRC8_8BIT(
DATA,
CRC_OUT,
RESET,
ENABLE,
CLK);
input [7:0]DATA;
input RESET;
input ENABLE;
input CLK;
output [7:0] CRC_OUT;
wire [7:0]DATA
wire RESET;
wire ENABLE
wire CLK
wire [7:0] CRC_OUT;

assign CRC_OUT = LFSR_N;

reg [7:0] LFSR_N
reg [7:0] LFSR_S;

always@(*) begin
    LFSR_S[0] = DATA[0]^DATA[1]^DATA[3]^DATA[6]^DATA[7]^LFSR_N[0]^ LFSR_N[1]^LFSR_N[3]^LFSR_N[6]^LFSR_N[7];
    LFSR_S[1] = DATA[1]^DATA[2]^DATA[4]^DATA[7]^LFSR_N[1]^ LFSR_N[2]^LFSR_N[4]^LFSR_N[7];
    LFSR_S[2] = DATA[0]^DATA[1]^DATA[2]^DATA[5]^DATA[6]^DATA[7]^LFSR_N[0]^ LFSR_N[1]^LFSR_N[2]^LFSR_N[5]^LFSR_N[6]^LFSR_N[7];
    LFSR_S[3] = =DATA[1]^DATA[2]^DATA[3]^DATA[6]^DATA[7]^ LFSR_N[1]^LFSR_N[2]^LFSR_N[3]^LFSR_N[6]^LFSR_N[7];
    LFSR_S[4] = DATA[0]^DATA[1]^DATA[2]^DATA[4]^DATA[6]^LFSR_N[0]^ LFSR_N[1]^LFSR_N[2]^LFSR_N[4]^LFSR_N[6];
    LFSR_S[5] = DATA[1]^DATA[2]^DATA[3]^DATA[5]^DATA[7]^ LFSR_N[1]^LFSR_N[2]^LFSR_N[3]^LFSR_N[5]^LFSR_N[7];
    LFSR_S[6] = DATA[0]^DATA[1]^DATA[2]^DATA[4]^DATA[7]^LFSR_N[0]^ LFSR_N[1]^LFSR_N[2]^LFSR_N[4]^LFSR_N[7];
    LFSR_S[7] = DATA[0]^DATA[2]^DATA[5]^DATA[6]^DATA[7]^LFSR_N[0]^ LFSR_N[2]^LFSR_N[5]^LFSR_N[6]^LFSR_N[7];
end

always@ (posedge CLK or posedge RESET) begin
    if(RESET) begin
        LFSR_N <= 8’ hff;
    else if (ENABLE) begin
        LFSR_N <= LFSR_S;
    end
end

endnodule

3、自动生成器

        上面推导其实较为麻烦，不过上面的方法其实可写成一个脚本，实现任意多项式任意位宽输入的并行CRC硬件电路。

        http://www.OutputLogic.com 有自动生成器，大家可以试试。