题目：

示例：

分析：

这题和本月出过的每日一题：两数之和，三数之和类似。

不夸张的说只要把三数之和的代码拿来再套层for循环改改就可以了。

不过我这里还是简单捋一捋思路，题目给一个数组，要求返回所有长度为4，总和为 target 的子数组（不用连续）。

比较容易想到的是暴力解法，直接套四层 for 循环，然后用 set（unordered_set）来接收满足条件的数组（用于去重），然后再一顿 for 循环把去重后的结果取出来放到 vector 中返回，没试过这种解法，但是中等题大多不能使用暴力解法，会超时。

我们可以先将原数组直接排序（这里是题目要求返回元素值，如果是要返回数组索引，则不能直接排序，需要有别的操作，以后遇到再详细说），然后数组就从小到大排序了（从大到小也可以）。

我们可以使用两个指针分别指向数组首尾，他们的和如果小于 target ，那么就把左指针右移（由于数组是从小到大排序，因此左指针右移则一定会将双指针之和变大，变得更接近target），如果他们的和大于 target ，那么就把右指针左移（原因同上）。 

这样，我们就解决了“两数之和”，可是我们这是四数之和呀，其实大差不差，我们只需要固定住四数中的“前两数”，然后再使用双指针来寻找两数之和即可，即在数组开头固定住两个指针a和b。然后使用双指针找到targte减去a和b所指元素之和即可。本题和三数之和不同的地方就在于三数之和只需固定“前一数”，而四数之和多固定一个数而已。

另外就是去重，排序原数组的原因，一是可以使用双指针来寻找 target ，二就是去重。

如果固定的前两数中，有遇到和上一次相同的数则跳过本次循环，例如示例二：

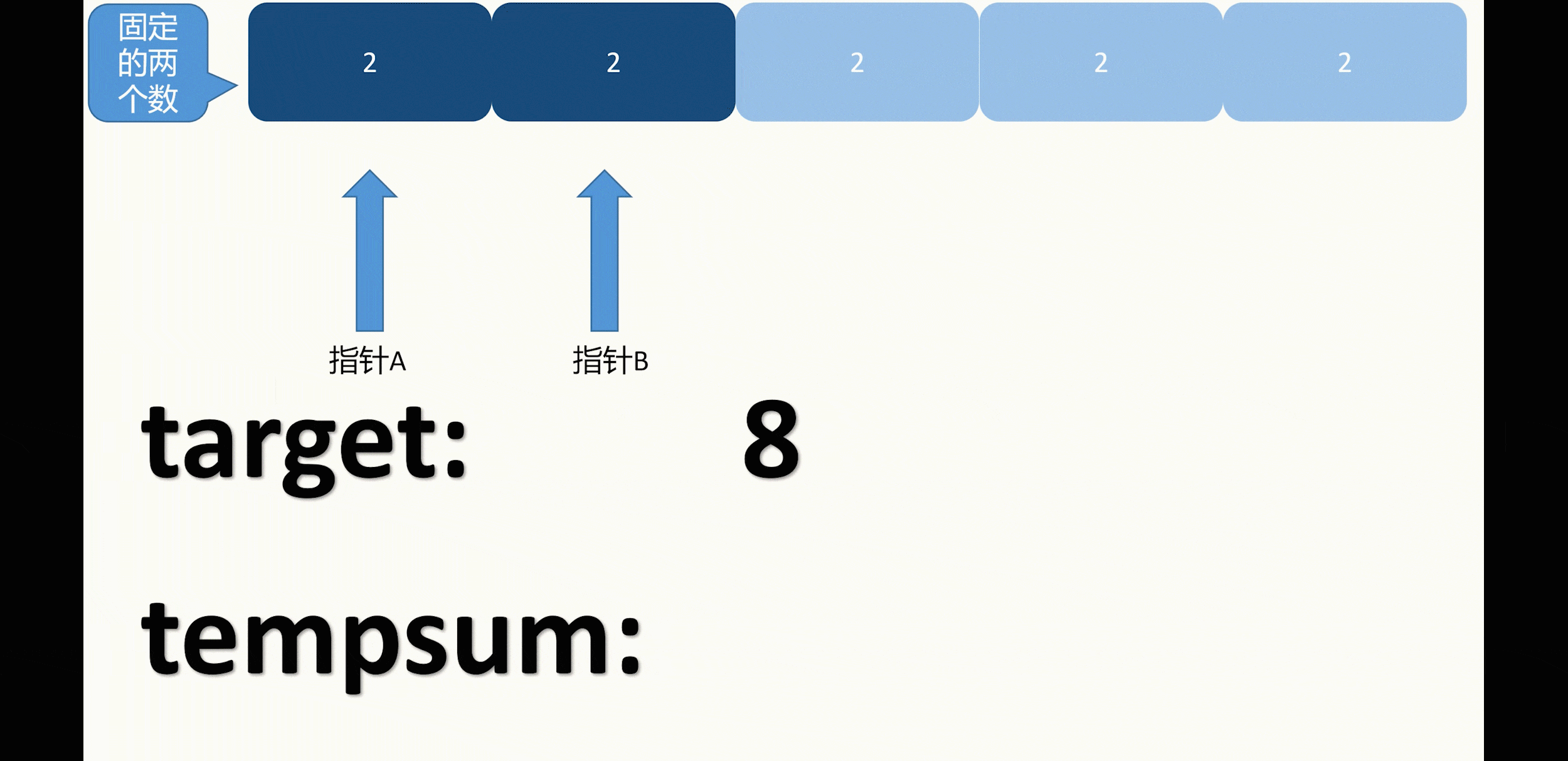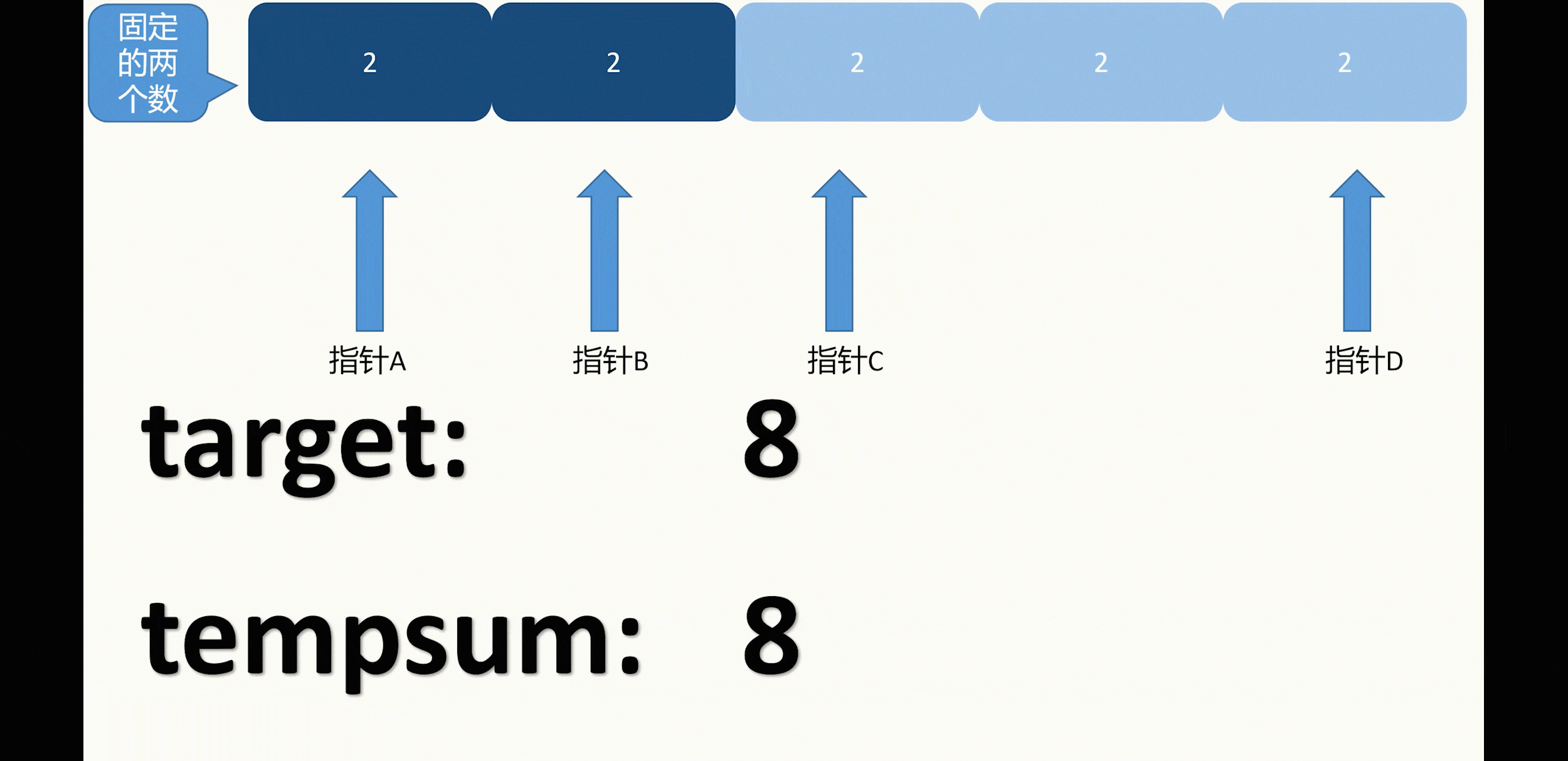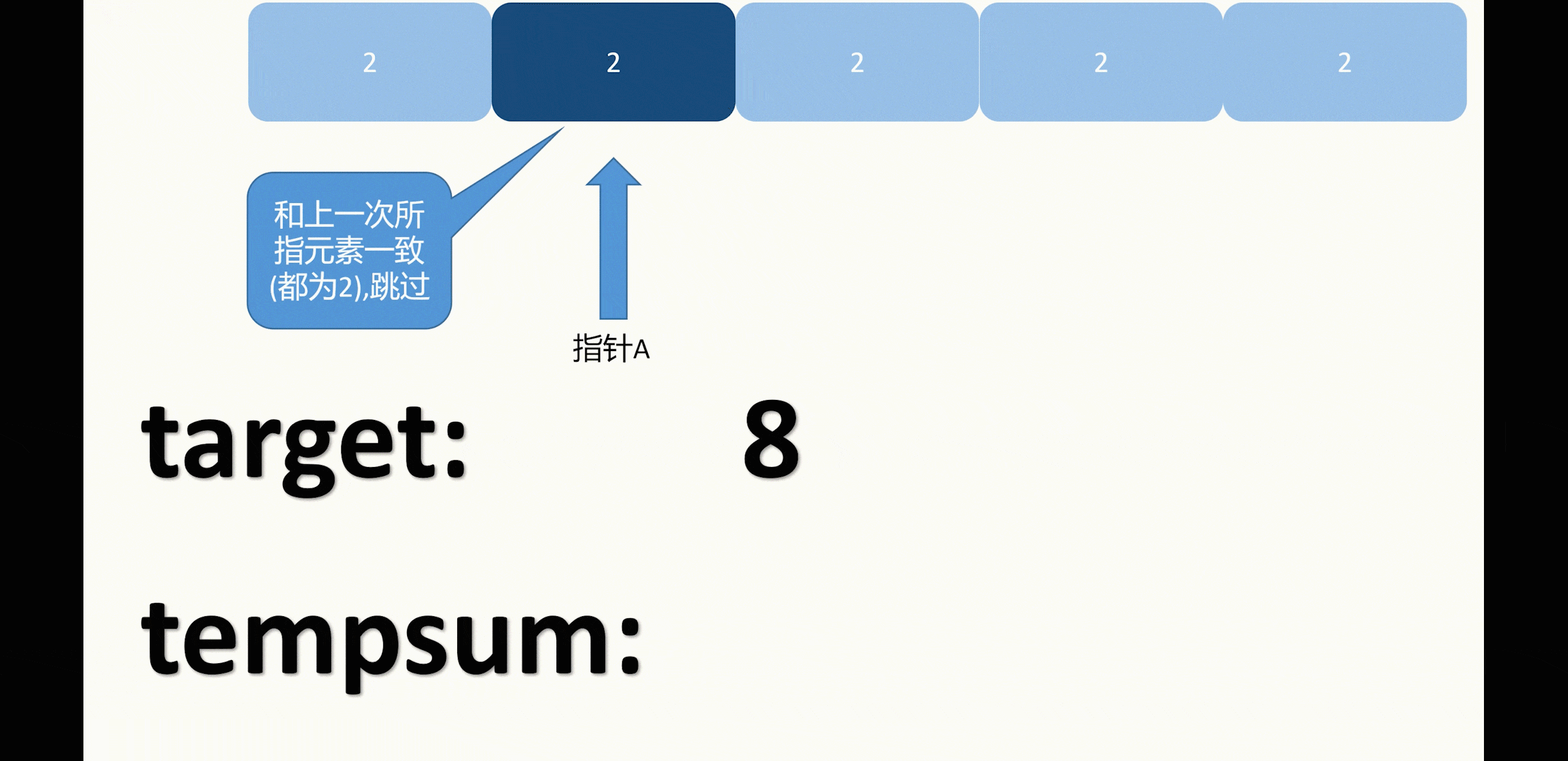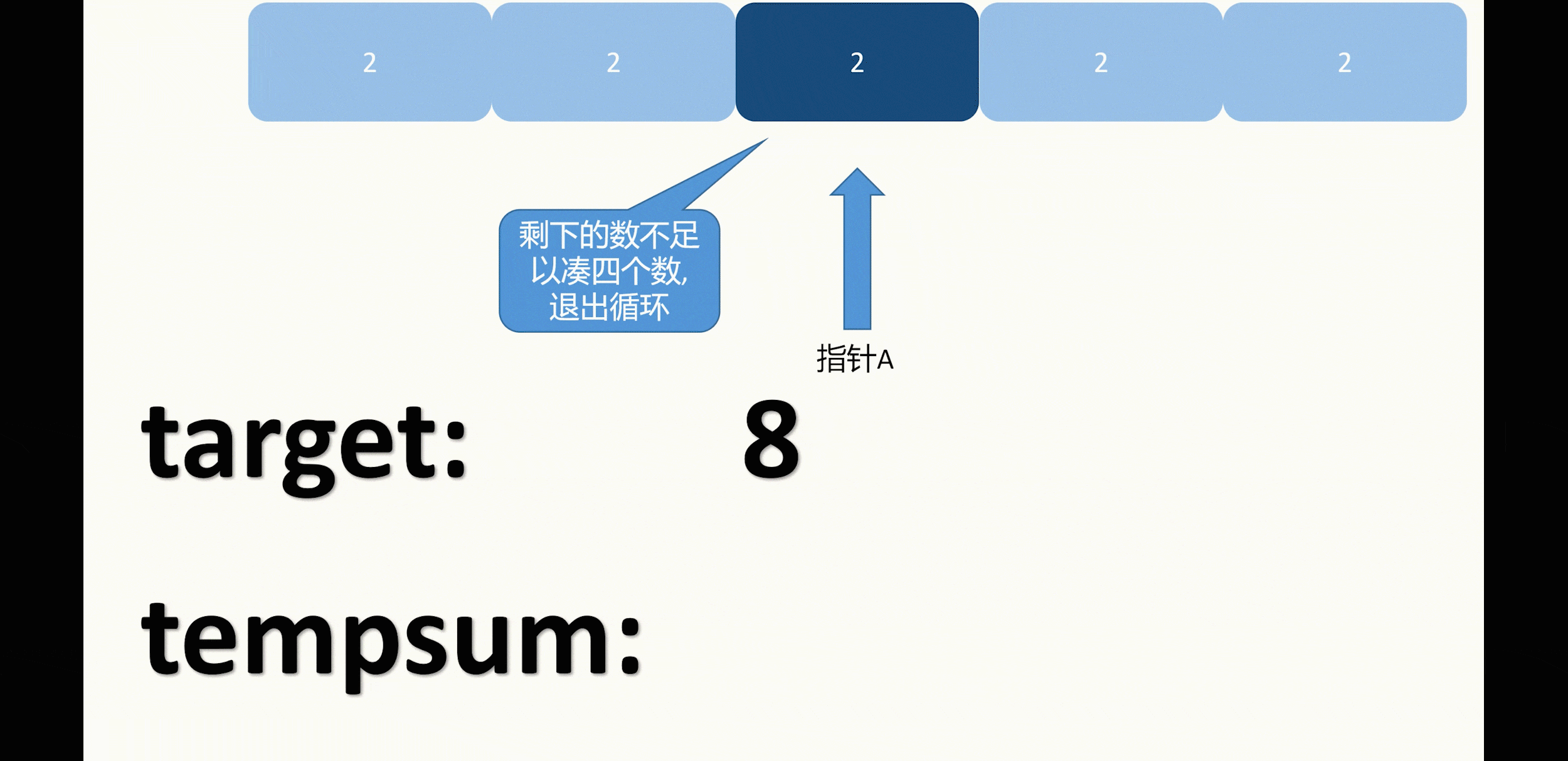
并且如果双指针所指的元素和上一次所指的元素一致，也是需要跳过的（这一点在下面代码中体现）。

代码+运行结果：

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        vector<vector<int>>res;
        if(nums.size()<4) return res;
        sort(nums.begin(),nums.end());
        int c,d;
        for(int a=0;a<nums.size()-3;a++){
            if(a>0 && nums[a]==nums[a-1]) continue; //去重
            for(int b=a+1;b<nums.size()-2;b++){
                if(b>a+1 && nums[b]==nums[b-1]) continue;   //去重  
                c=b+1,d=nums.size()-1;
                while(c<d){
                    long tempsum=(long)nums[a]+(long)nums[b]+(long)nums[c]+(long)nums[d];
                    if(target==tempsum){
                        res.push_back(vector<int>{nums[a],nums[b],nums[c],nums[d]});
                        //去重  
                        int tc=nums[c],td=nums[d];
                        while(c<d && nums[c]==tc) c++;  
                        while(c<d && nums[d]==td) d--;
                    }else if(target>tempsum){
                        c++;
                    }else{
                        d--;
                    }
                }
            }
        }
        return res;
    }
};