1143.最长公共子序列

题目链接
解题思路： 动规五部曲分析如下：

1.确定dp数组（dp table）以及下标的含义

dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]

2.确定递推公式

主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同

如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;

如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。

即：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);

代码如下：

if (text1[i - 1] == text2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}

3.dp数组如何初始化

先看看dp[i][0]应该是多少呢？

test1[0, i-1]和空串的最长公共子序列自然是0，所以dp[i][0] = 0;

同理dp[0][j]也是0。

其他下标都是随着递推公式逐步覆盖，初始为多少都可以，那么就统一初始为0。

代码：

vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));

4.确定遍历顺序

从递推公式，可以看出，有三个方向可以推出dp[i][j]，如图：

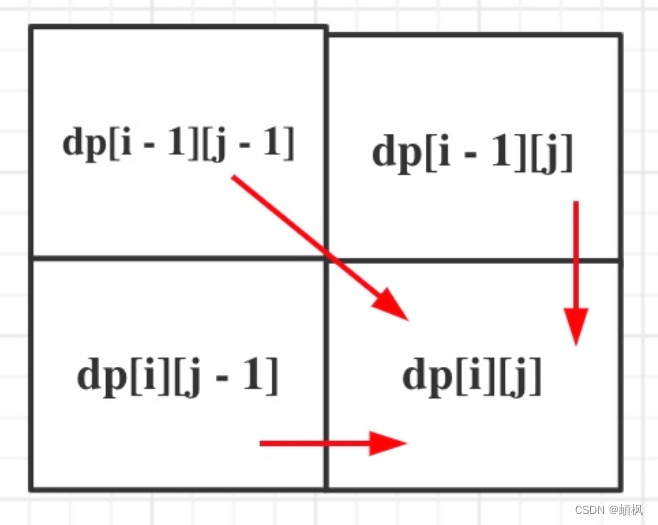
那么为了在递推的过程中，这三个方向都是经过计算的数值，所以要从前向后，从上到下来遍历这个矩阵。

5.举例推导dp数组

以输入：text1 = “abcde”, text2 = “ace” 为例，dp状态如图：

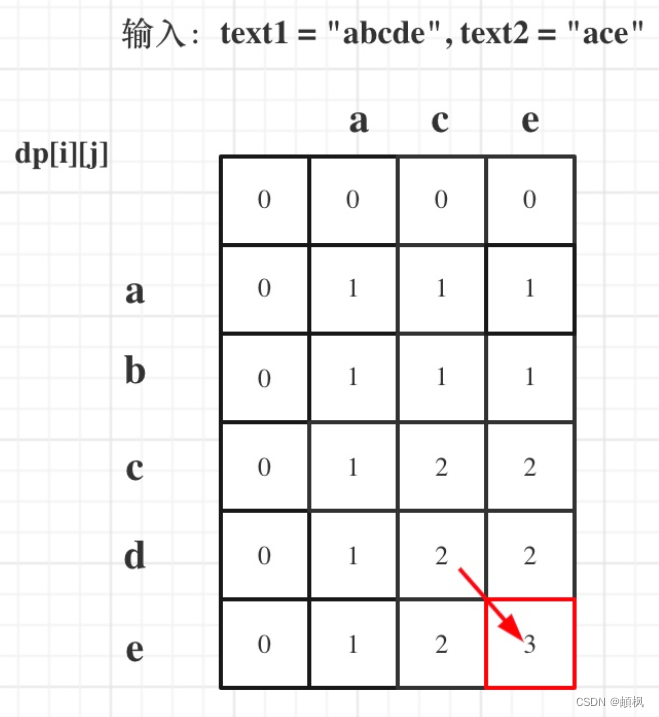
最后红框dp[text1.size()][text2.size()]为最终结果

以上分析完毕，C++代码如下：

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));
        for (int i = 1; i <= text1.size(); i++) {
            for (int j = 1; j <= text2.size(); j++) {
                if (text1[i - 1] == text2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[text1.size()][text2.size()];
    }
};

---

1035.不相交的线

题目链接
解题思路：
本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！
那么本题就和我们刚刚讲过的上一题就是一样一样的了，代码也是一样的。

class Solution {
public:
    int maxUncrossedLines(vector<int>& A, vector<int>& B) {
        vector<vector<int>> dp(A.size() + 1, vector<int>(B.size() + 1, 0));
        for (int i = 1; i <= A.size(); i++) {
            for (int j = 1; j <= B.size(); j++) {
                if (A[i - 1] == B[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[A.size()][B.size()];
    }
};

---

53. 最大子序和

题目链接
**解题思路：**动规五部曲如下：

1.确定dp数组（dp table）以及下标的含义

dp[i]：包括下标i（以nums[i]为结尾）的最大连续子序列和为dp[i]。

2.确定递推公式

dp[i]只有两个方向可以推出来：

dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和
nums[i]，即：从头开始计算当前连续子序列和

一定是取最大的，所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);

3.dp数组如何初始化

从递推公式可以看出来dp[i]是依赖于dp[i - 1]的状态，dp[0]就是递推公式的基础。

dp[0]应该是多少呢?

根据dp[i]的定义，很明显dp[0]应为nums[0]即dp[0] = nums[0]。

4.确定遍历顺序

递推公式中dp[i]依赖于dp[i - 1]的状态，需要从前向后遍历。

5.举例推导dp数组

以示例一为例，输入：nums = [-2,1,-3,4,-1,2,1,-5,4]，对应的dp状态如下

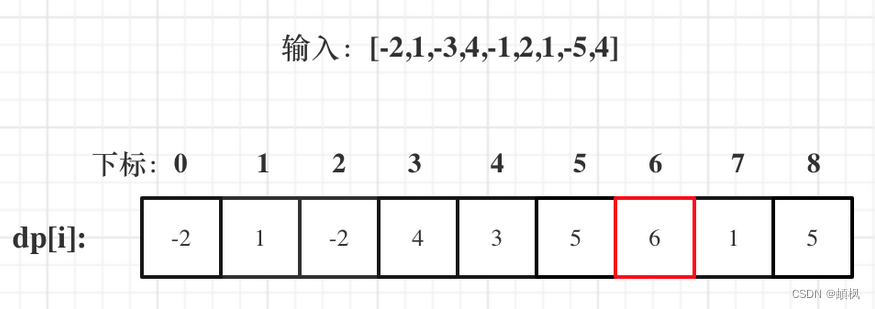
注意最后的结果可不是 dp[nums.size() - 1]！ ，而是dp[6]。

在回顾一下dp[i]的定义：包括下标i之前的最大连续子序列和为dp[i]。

那么我们要找最大的连续子序列，就应该找每一个i为终点的连续最大子序列。

所以在递推公式的时候，可以直接选出最大的dp[i]。

以上动规五部曲分析完毕，完整代码如下：

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        vector<int> dp(nums.size());
        dp[0] = nums[0];
        int result = dp[0];
        for (int i = 1; i < nums.size(); i++) {
            dp[i] = max(dp[i - 1] + nums[i], nums[i]); // 状态转移公式
            if (dp[i] > result) result = dp[i]; // result 保存dp[i]的最大值
        }
        return result;
    }
};