1.内容
建议再看这节之前能对C++有一定了解
二叉树在前面C的数据结构阶段时有出过,现在我们对二叉树来学习一些更复杂的类型,也为之后C++学习的 map 和 set 做铺垫
- 1. map和set特性需要先铺垫二叉搜索树,而二叉搜索树也是一种树形结构
- 2. 二叉搜索树的特性了解,有助于更好的理解map和set的特性
- 3. 有些OJ题使用C语言方式实现比较麻烦,比如有些地方要返回动态开辟的二维数组。
因此本节文章所涉及到的知识点有很多都会与C++有关
2.搜索二叉树:
🍉搜索二叉树的概念:
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
🍉搜索二叉树的操作

int a[ ] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
🍒二叉搜索树的查找
- 1. 从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
- 2. 最多查找高度次,走到到空,还没找到,这个值不存在。
🍒搜索二叉树的插入:
插入的具体过程如下:
- 1. 树为空,则直接新增节点,赋值给root指针
- 2. 树不空,按二叉搜索树性质查找插入位置,插入新节点
🍒搜索二叉树的删除
删除时搜索二叉树最复杂的地方,他只要分为三种情况:
1. 删除叶子节点
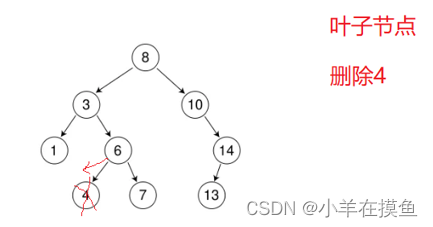
也就是左右都无孩子的节点,直接删除就行
2. 删除只有一个孩子的节点

左孩子为空,或者右孩子为空
这种情况需要将他们的下一个孩子节点接到其父节点上
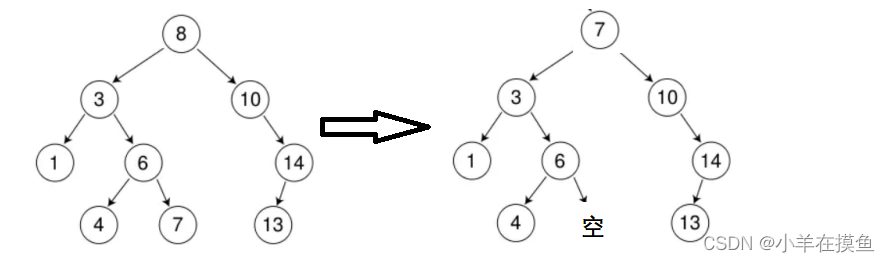
3.删除两边都有孩子的节点
如删除 8 或者 3
这种清空就比较复杂,我们用替换原则,找左树的最大节点或者去找右树的最小节点来替换。
比如我们要删除8,就需要找左树的最大节点进行替换,左树的最大节点是7,我们将其与放到8的位置,将6的右节点置为空即可
🍉搜索二叉树的实现:
1.创建:
template<class K>
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key) //初始化列表进行初始化
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};2. 插入操作:
bool Insert(const K& key)
{
// 1.先判断跟为空
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
// 利用循环判断cur节点的值与插入值的大小,来缺点插入值放到哪
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
// 新创建一个节点放入插入值
cur = new Node(key);
// 将新节点进行链接
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}3.查找操作:
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}4.打印操作:
// 利用递归打印,因为类外拿不到_root,
// 所以给递归又加了个嵌套函数,用该类内的函数去调_root
void InOrder()
{
_InOrder(_root);
cout << endl;
}
// 直接写这个函数,在类外面不能调_root,所以传参比较困难
// 因为_root是私有成员,所以序号再套上面的一层函数
void _InOrder(Node* root)
{
if (root == nullptr)
return;
// 中序遍历的逻辑打印
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}5.删除操作
上面所说的删除叶子节点的情况,可以直接放到入到第二种情况下一并解决,
在第二种情况的时候需要注意:

这种情况要去判断要删除的节点是否为根节点,如果是就直接把下面的孩子节点换成根节点就行
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = Find(key);
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 删除
// 1、左为空
// 如果此时根节点只有一个孩子,此时要删除根节点,
// 就不会进入之前的判断,会导致parent为空的空指针问题
// 可看上图了解
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
// 2、右为空
// 如果此时根节点只有一个孩子,此时要删除根节点,
// 就不会进入之前的判断,会导致parent为空的空指针问题
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else
{
// 找右树最小节点替代,也可以是左树最大节点替代
// 这里我们用的是右数的最小节点
Node* pminRight = cur; // pminRight是minRight的父节点
Node* minRight = cur->_right;
while (minRight->_left)
{
pminRight = minRight;
minRight = minRight->_left;
}
cur->_key = minRight->_key;
if (pminRight->_left == minRight)
{
pminRight->_left = minRight->_right;
}
else
{
pminRight->_right = minRight->_right;
}
delete minRight;
}
return true;
}
}
return false;
}🍒源代码如下
#include <iostream>
using namespace std;
template<class K>
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
// 插入
bool Insert(const K& key)
{
// 1.先判断跟为空
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
// 利用循环判断cur节点的值与插入值的大小,来缺点插入值放到哪
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
// 新创建一个节点放入插入值
cur = new Node(key);
// 将新节点进行链接
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
// 查找
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
// 删除
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = Find(key);
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 删除
// 1、左为空
// 如果此时根节点只有一个孩子,此时要删除根节点,
// 就不会进入之前的判断,会导致parent为空的空指针问题
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
// 2、右为空
// 如果此时根节点只有一个孩子,此时要删除根节点,
// 就不会进入之前的判断,会导致parent为空的空指针问题
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else
{
// 找右树最小节点替代,也可以是左树最大节点替代
Node* pminRight = cur; // pminRight是minRight的父节点
Node* minRight = cur->_right;
while (minRight->_left)
{
pminRight = minRight;
minRight = minRight->_left;
}
cur->_key = minRight->_key;
if (pminRight->_left == minRight)
{
pminRight->_left = minRight->_right;
}
else
{
pminRight->_right = minRight->_right;
}
delete minRight;
}
return true;
}
}
return false;
}
// 打印
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
private:
Node* _root = nullptr;
};
//测试
void TestBSTree()
{
int a[] = { 8, 3, 1, 6, 4, 7, 10, 14, 13 };
BSTree<int> t1;
// 循环插入
for (auto e : a)
{
t1.Insert(e);
}
t1.InOrder();
t1.Erase(13);
t1.Erase(14);
t1.Erase(10);
t1.Erase(4);
t1.Erase(6);
t1.Erase(3);
t1.InOrder();
}
int main()
{
TestBSTree();
return 0;
}3.搜索二叉树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:

最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:
最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:
如果退化成单支树,二叉搜索树的性能就失去了。
那能否进行改进,不论按照什么次序插 入关键码,二叉搜索树的性能都能达到最优?
所以我们后面还会对AVL树和红黑树做为重点学习