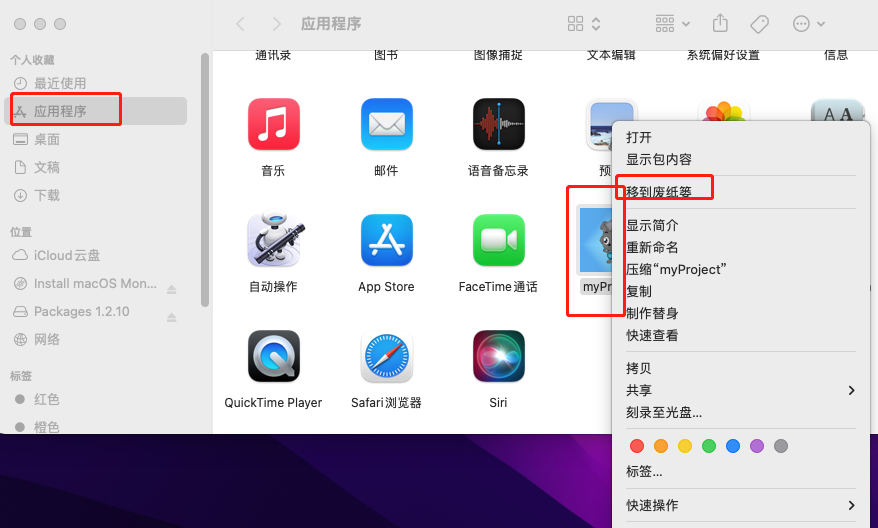
峰度(Kurtosis)与偏态(Skewness)就是量测数据正态分布特性的两个指标。
- 峰度(Kurtosis)
峰度衡量数据分布的平坦度(flatness),即数据取值分布形态陡缓程度的统计量。它是和正太分布相比较的。尾部大的数据分布,其峰度值较大。正态分布的峰度值为3。
计算公式如下:
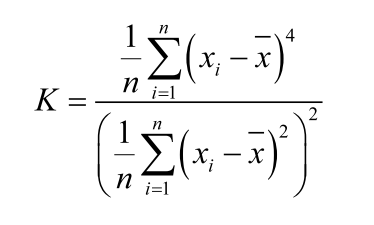
式中, K表示峰度(无量纲); i表示第 i个数值; xbar表示平均值; n是采样数量。
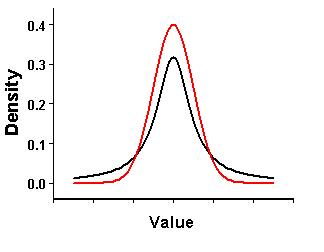
图1 峰度(Kurtosis)示意图
图 1所示,黑线服从尖峰(leptokurtic)、厚尾(thick-tailed)分布的峰度值大于3。红线服从正态分布,峰度值等于3。
峰度kurtosis:用于度量x偏离某分布的程度。
- 正太分布的峰度是3;
- 当时间序列的曲线峰值比正太分布的高时,峰度大于3,即呈现尖峰分布;
- 当比正太分布的低时,峰度小于3,即呈现峰值比较平坦。
注意:个别的软件会将峰度值减3,ArcGIS默认正态分布的峰度为3。MS Excel的计算公式与上面略有不同。
2. 偏态(Skewness)
偏态量度对称性。0说明是最完美的对称性,正态分布的偏态就是0。
偏态的计算公式如下
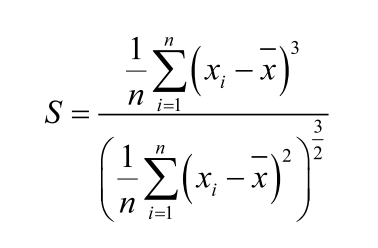
式中, S表示偏度(无量纲);i 表示第 i个数值; xbar表示平均值; n是采样数量。
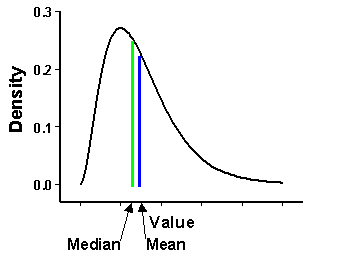
图2 偏态(Skewness)示意图
如图2所示,右偏态为正,表明平均值大于中位数。反之为左偏态,为负。
偏度skewness:用于衡量x的对称性。
- 对于正太分布,偏度为0;
- 若偏度为正,则x均值左侧的离散度比右侧弱;
- 若偏度为负,则x均值左侧的离散度比右侧强。
如下是MATLAB代码展示kurtosis函数和skewness函数使用:
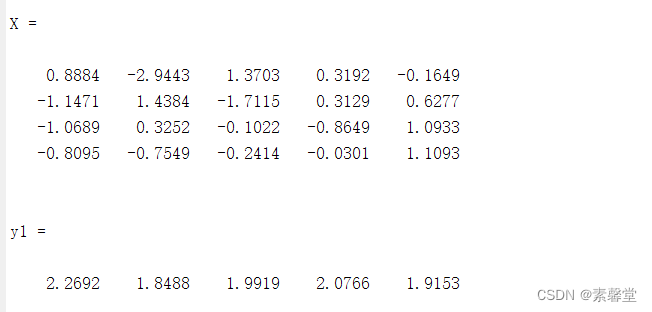
代码及结果运行
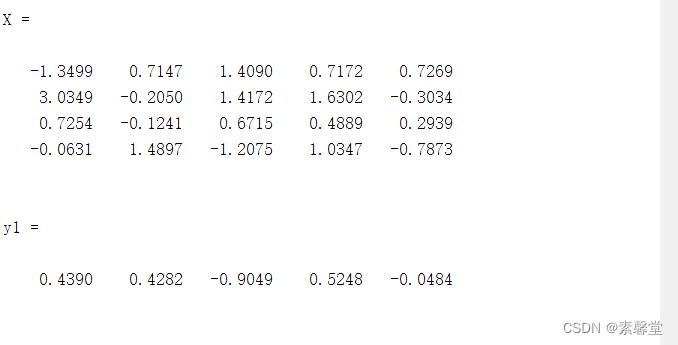
%% 偏斜度
clear all;
X=randn([4,5])
y1=skewness(X)
%% 峰度
clear all;
X=randn([4,5])
y1=kurtosis(X)