基本思想
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
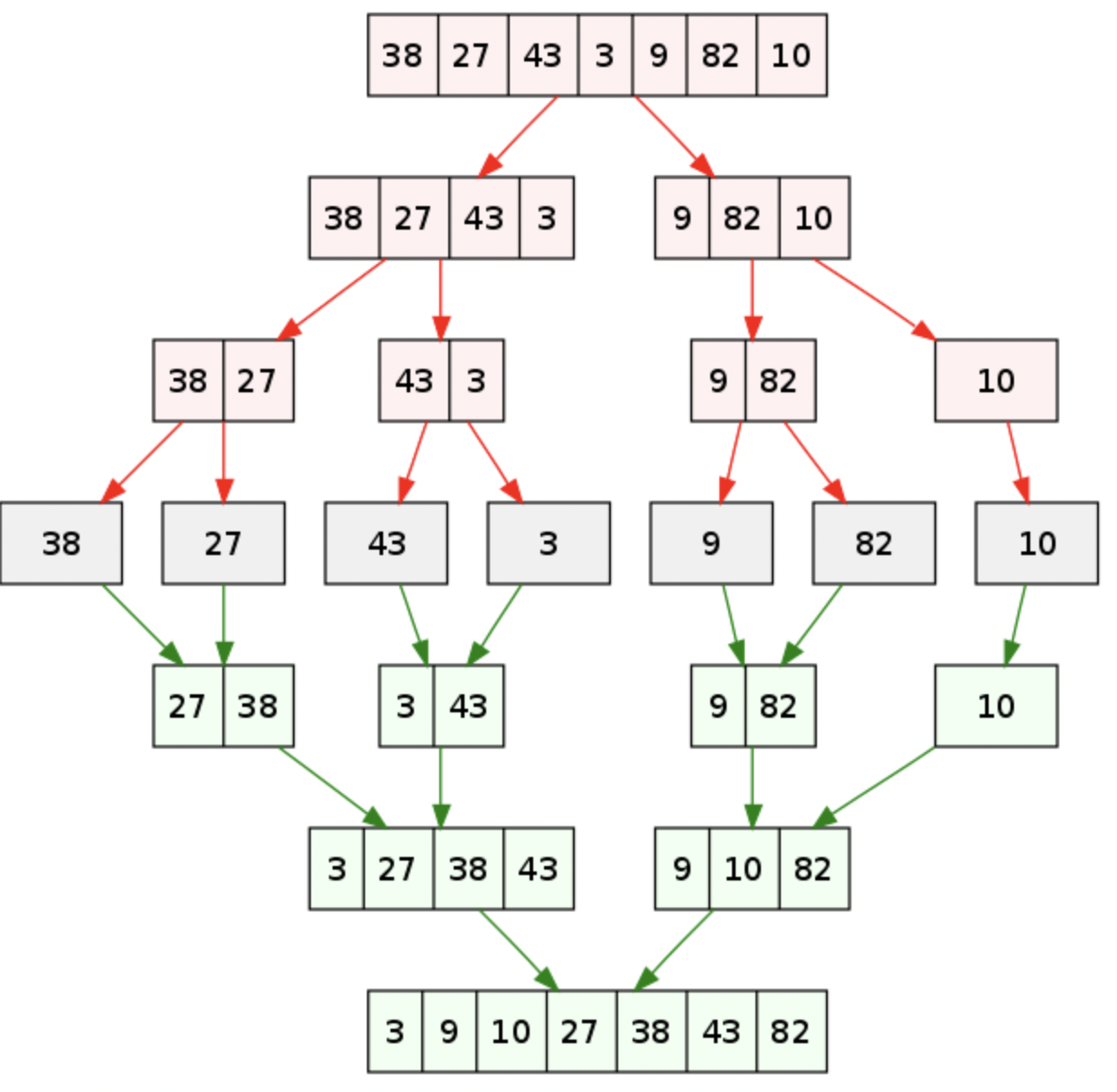
归并排序其实就是等分分割数组,直到分割后的数组有序再将这分割的两个数组归并到一个新的数组里,再拷贝到原数组中。这里就与二叉树的后序遍历极为相似,分割的数组只有一个数时就默认有序了,再合并之后一步步的递归回去。
代码(递归)
void _MergeSort(int* arr, int left, int right,int* tmp)
{
if (left == right)//不可能分割出不存在的区间
return;
int midi = (left + right) / 2;
_MergeSort(arr, left, midi, tmp);//分割归并左部分
_MergeSort(arr, midi + 1, right, tmp);//分割归并右部分
//归并(begin1和end2之间的数)即left和right之间的数
int i = 0;//临时数组下标
int begin1 = left, end1 = midi;
int begin2 = midi + 1, end2 = right;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
tmp[i++] = arr[begin1++];
else
tmp[i++] = arr[begin2++];
}
while (begin1 <= end1)
{
tmp[i++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = arr[begin2++];
}
memcpy(arr+left, tmp, sizeof(int) * i);//归并一次就拷贝一次
}void MergeSort(int* arr, int left, int right)
{
int* tmp = (int*)malloc(sizeof(int*) * (right + 1));
_MergeSort(arr, 0, right,tmp);
free(tmp);
}代码1(非递归)
void _MergeSort(int* arr, int left, int right, int* tmp)
{
int gap = 1;//每一组的数据个数
while (gap < right)
{
for (int i = 0; i <= right; i += 2 * gap)//两两归并,遍历整个数组
{
int j = 0;//临时数组的下标
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
if (end1 > right || begin2 > right)
break;
if (end2 > right)
{
end2 = right;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
tmp[j++] = arr[begin1++];
else
tmp[j++] = arr[begin2++];
}
while (begin1 <= end1)
{
tmp[j++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = arr[begin2++];
}
memcpy(arr + i, tmp, sizeof(int) * j);//归并一次拷贝一次
}
gap *= 2;
}
}非递归就要知道该代码原来递归是怎么走的,递归的部分实际上是在一直分割成两部分,直到不能再分割了以后,就开始合并到tmp临时数组里,所以非递归的写法实际就也是分组执行,先是单个数是一组,两两一组进行比较拷贝,原先拷贝好的就可以是一组了,此时每组就有两个数是有序的,再两两一组,两组再进行拷贝,此时拷贝好的一组就有四个有序的数了,再进行四四一组.......
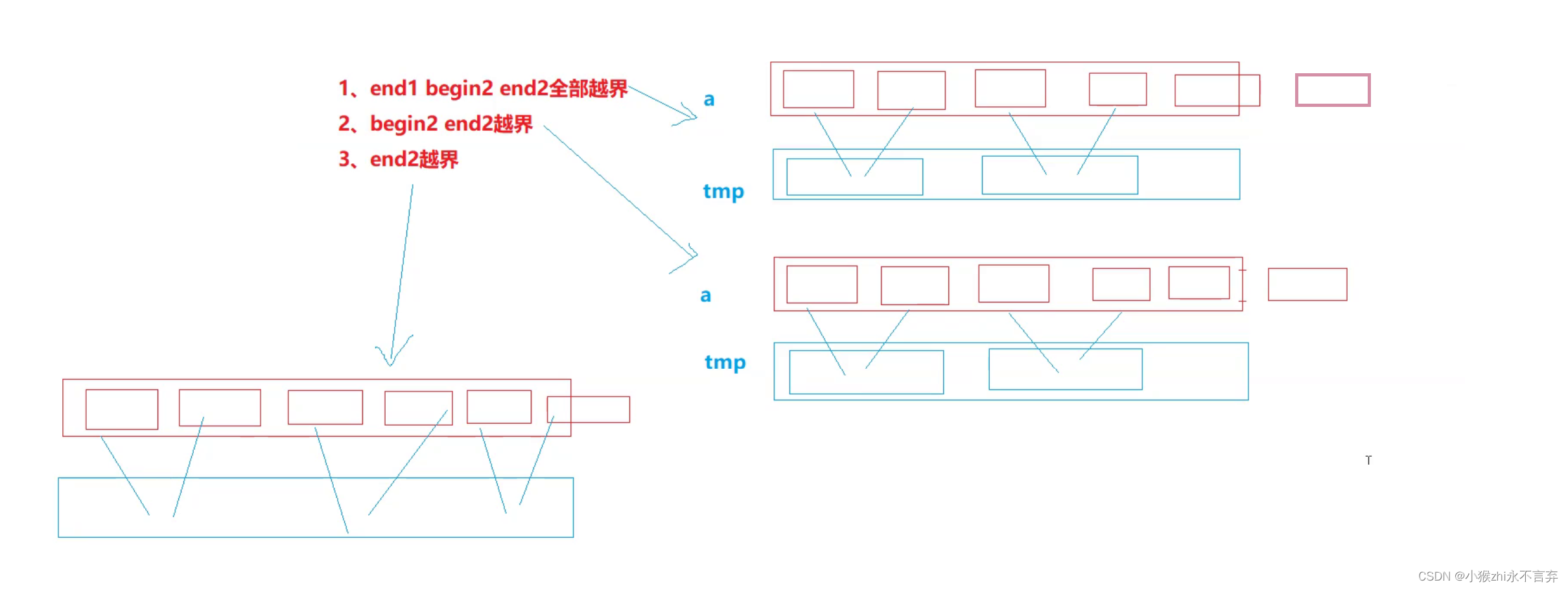
但是这可能存在越界的情况,两组数据拷贝,极有可能就越界,而且存在三种越界的情况:
而上面的一二两种情况又可以看作一种:多余了已经有序的一组(不到一组)此时该组已经有序了,所以也不用进行归并了,直接放在原数组中就行了,但是你memcpy拷贝数组就得一组组的拷贝了,不能归并完整个数组以后再全部拷贝到原数组。
而第三种情况就是多了不仅仅一组的数据但是却又不够两组,此时就不能说这一组半是有序的,所以就重行划区间,end2就指向最后一个数的下标,将这半组也看成一组,两两拷贝数据成有序。
代码2(非递归)
void _MergeSort(int* arr, int left, int right, int* tmp)
{
int gap = 1;//每一组的数据个数
while (gap < right)
{
int j = 0;//临时数组下标
for (int i = 0; i <= right; i += 2 * gap)//两两归并整个数组
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
if (end1 > right)
{
end1 = right;
begin2 = end2 + 1;//不存在的区间
}
else if(begin2 > right)
{
begin2 = end2 + 1;//不存在的区间
}
else if (end2 > right)
{
end2 = right;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
tmp[j++] = arr[begin1++];
else
tmp[j++] = arr[begin2++];
}
while (begin1 <= end1)
{
tmp[j++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = arr[begin2++];
}
}
memcpy(arr, tmp, sizeof(int) * j);//一次拷贝整个数组数据
gap *= 2;
}
}这就是可以一次拷贝整个数组的情况,即当遇到越界的情况就就调整范围,继续拷贝。