寻找网络1020的结构平衡点

( A, B )---2*n*2---( 1, 0 )( 0, 1 )

用网络分类A和B，让A是（0，1）（0，0），让B是（1，0）（0，0）。记为网络1020.AB的测试集均为（0，0）（0，1）（1，0）（1，1）. 由训练集可知（0，1）应被分为A，（1，0）应被分为B。（0，0）（1，1）的分类有三种可能，或者都是对半分，分类准确率为0.25+0.25=0.5，0.25+0.25=0.5。或者有一个是对半分，分类准确率为0.25+0.25+0.125=0.625，0.25+0.125=0.375。或者都被分为A或B，分类准确率为0.25+0.25+0.25=0.75，0.25

所以这个网络峰值分类准确率只可能为0.5，0.5；0.625，0.375；0.75，0.25.这三种情况。寻找实现峰值的隐藏层节点数。

首先让n=2

0	1		1	0		1b	1
0	0		0	0		0	0
		1020	2
f2[0]	f2[1]	迭代次数n	p-ave	1-0	0-1	δ	耗时ms/次	耗时ms/199次
0.52257	0.47743	91936.1	0.5	0.61935	0.38065	9.00E-04	89.4523	17816
0.43729	0.56271	103144	0.5	0.60302	0.39698	8.00E-04	100.437	19987
0.53262	0.46738	117455	0.5	0.62186	0.37814	7.00E-04	111.623	22229
0.50753	0.49247	136592	0.5	0.6206	0.3794	6.00E-04	128.94	25659
0.46737	0.53263	163353	0.5	0.6093	0.3907	5.00E-04	154.095	30665

0	194	5	38.8
11	92	107	0.85981
											199
A	4		B			A	1		B
0	0	0	0	0	0	0	0	0	0	0	0
1	0	1	1	0	1	1	0	1	1	0	1
2	1	0	2	1	0	2	1	0	2	1	0
3	1	1	3	1	1	3	1	1	3	1	1


A	103		B			A	91		B
0	0	0	0	0	0	0	0	0	0	0	0
1	0	1	1	0	1	1	0	1	1	0	1
2	1	0	2	1	0	2	1	0	2	1	0
3	1	1	3	1	1	3	1	1	3	1	1

4	1	023
1	13	02
103	01	23
91	013	2

有4次1被分类为A，023被分为B。1次13被分为A，02被分为B。103次01被分为A，23被分为B。91次013被分为A，2被分为B。

00	194	5		38.8
11	92	107		0.85981

194次（0，0）被分为A，5次被分为B，比例为38.8.（1，1）接近被对半分。

再让n分别等于5，10，15，20，25，…，550，分别计算（0，0）（1，1）被分为A和B的比例。得到表格

A/B	2	5	10	15	20	25	30	35	40	45	50	55	60	70	80	90	100	120
(0,0)	38.8	1.0947	1.5513	2.4912	3.975	4.3784	3.975	3.523	4.528	5.419	4.237	7.292	6.37	8.045	6.37	6.37	9.474	9.474
(1,1)	0.8598	0.8426	0.932	0.99	0.8952	0.951	0.809	0.97	1.073	1.187	1.341	1.187	1.01	1.095	0.913	1.031	1.163	1.095

A/B	140	160	180	200	220	240	260	280	300	320	340	360	380	400	450	500	550
(0,0)	7.2917	7.2917	9.4737	8.4762	5.6333	6.1071	5.219	4.528	4.237	3.975	2.827	2.827	2.98	2.902	2.373	3.422	1.223
(1,1)	1.3976	1.6184	2.1587	1.6892	1.6892	2.2623	2.317	2.062	2.827	5.03	1.369	1.261	1.236	1.187	1.031	1.163	1.152

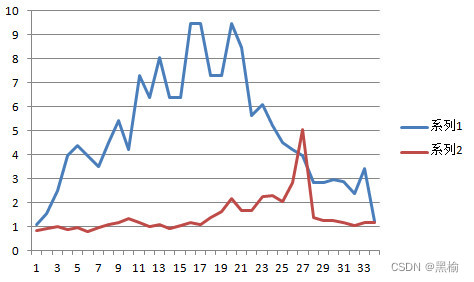
当n=2时（0，0）的分配比例出现峰值为38.8，此时（1，1）的比例为0.859.这组数据很接近0.625，0.375的比例。若不考虑n=2，（0，0）的比例峰值为n=120，为9.474.此时（1，1）的比例为1.095.当n大于180以后（0，0）的比例迅速下滑。

统计1-0位分类准确率

	2	5	10	15	20	25	30	35	40	45	50	55	60	70	80	90	100	120
δ	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0
9.00E-04	0.6193	0.5088	0.5251	0.5528	0.5691	0.5729	0.573	0.598	0.573	0.594	0.587	0.568	0.592	0.611	0.606	0.611	0.608	0.616
8.00E-04	0.603	0.4987	0.5302	0.544	0.5678	0.5842	0.598	0.588	0.587	0.597	0.602	0.599	0.59	0.598	0.621	0.612	0.592	0.613
7.00E-04	0.6219	0.5101	0.5364	0.5603	0.5678	0.5892	0.568	0.56	0.575	0.597	0.595	0.592	0.606	0.616	0.603	0.611	0.599	0.612
6.00E-04	0.6206	0.4975	0.5251	0.5389	0.5779	0.5842	0.578	0.59	0.585	0.584	0.588	0.58	0.593	0.582	0.597	0.592	0.604	0.592
5.00E-04	0.6093	0.495	0.5226	0.5528	0.5678	0.5754	0.562	0.568	0.584	0.597	0.595	0.606	0.592	0.603	0.585	0.593	0.611	0.607


	140	160	180	200	220	240	260	280	300	320	340	360	380	400	450	500	550
δ	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0	1-0
9.00E-04	0.6156	0.6093	0.6357	0.6231	0.6244	0.642	0.666	0.651	0.681	0.676	0.58	0.575	0.578	0.58	0.533	0.572	0.607
8.00E-04	0.6055	0.6294	0.6269	0.6131	0.6382	0.6482	0.655	0.636	0.667	0.682	0.592	0.601	0.572	0.589	0.539	0.578	0.557
7.00E-04	0.6219	0.6281	0.6407	0.6219	0.6281	0.6369	0.631	0.638	0.682	0.643	0.607	0.58	0.567	0.565	0.555	0.59	0.554
6.00E-04	0.6005	0.6231	0.603	0.6281	0.6219	0.6457	0.639	0.646	0.666	0.651	0.585	0.565	0.558	0.539	0.557	0.563	0.587
5.00E-04	0.6156	0.6244	0.647	0.6307	0.6193	0.6382	0.634	0.623	0.637	0.658	0.579	0.574	0.575	0.572	0.553	0.578	0.562

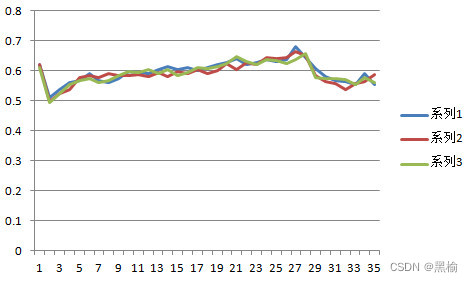
分类准确率的峰值出现在n=320.为65.8%。当n超过320以后分类准确率迅速下降。

统计迭代次数

	2	5	10	15	20	25	30	35	40	45	50	55	60	70	80	90	100	120
δ	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n
9.00E-04	91936	48767	33044	27967	25451	23789	22647	21876	21272	20743	20306	20001	19660	19266	18880	18596	18363	18002
8.00E-04	103144	53542	36770	30900	27975	26251	25150	24104	23420	22847	22405	21996	21728	21156	20746	20444	20172	19786
7.00E-04	117455	61460	41326	34623	31554	29404	28052	26956	26161	25509	25014	24514	24155	23609	23167	22838	22533	22073
6.00E-04	136592	70205	47383	39937	35874	33358	31835	30683	29766	29064	28418	27950	27439	26836	26261	25894	25587	25029
5.00E-04	163353	85621	55521	46584	41867	39242	37155	35697	34705	33799	33233	32602	32067	31302	30684	30180	29739	29155

	140	160	180	200	220	240	260	280	300	320	340	360	380	400	450	500	550
δ	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n
9.00E-04	17752	17542	17373	17240	17128	17032	16941	16867	16793	16735	16408	15198	14772	14543	13536	11617	11056
8.00E-04	19515	19279	19102	18948	18828	18718	18626	18533	18466	18394	19811	19667	16743	16355	12795	13289	13065
7.00E-04	21742	21486	21297	21123	20982	20870	20746	20659	20578	20499	21617	20194	16790	18063	15423	15277	14511
6.00E-04	24671	24376	24155	23951	23792	23671	23539	23433	23327	23252	24090	23078	20626	20847	16603	19349	14949
5.00E-04	28729	28357	28083	27831	27660	27501	27362	27229	27114	27015	26152	26161	23855	21500	20679	19402	19319

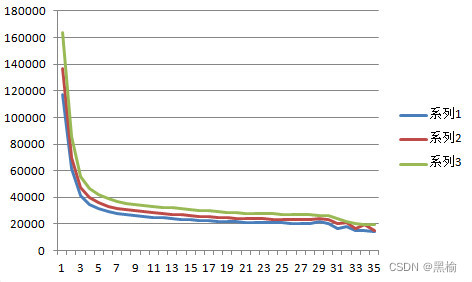
随着隐藏层节点数的增加，迭代次数一直在下降，当n=25的时候下降速度趋于平缓。n大于320后出现明显波动

统计迭代次数的标准差

	2	5	10	15	20	25	30	35	40	45	50	55	60	70	80	90	100	120	140
δ	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差
9.00E-04	354.45	5761.8	2396.7	1563.6	1203.5	865.62	652.8	595.5	543.8	482.9	436.7	388.7	344.9	294.9	254.2	204.8	199.1	160.6	139.3
8.00E-04	450.23	5055.5	2725	1831.7	1233.2	979.5	878.5	607.5	576.7	507.5	491.7	410.2	433.8	334.7	269.9	226.4	203.7	165.4	148.1
7.00E-04	373.85	6798.9	2834.2	1791.5	1331.4	1059.1	926.3	799.6	694.2	606.5	540.7	451.3	438.8	355.7	313.2	271	254.7	191.6	158.2
6.00E-04	293.19	6612.8	3154	2094.9	1653.9	1237.7	985.4	885.6	767.2	711.3	577.2	524.8	417	446.2	349.3	316.4	282.4	219.6	192.6
5.00E-04	348.82	11378	3657.1	2522	2073.1	1451	1223	980.5	895.1	770.8	658.7	681.7	608.2	505.8	408	379.9	332.5	255.9	235.1

	160	180	200	220	240	260	280	300	320	340	360	380	400	450	500	550
δ	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差	迭代次数标准差
9.00E-04	114.57	94.107	93.394	78.296	66.341	58.815	57.46	48.07	45.48	8952	10584	11000	11023	10444	9766	8954
8.00E-04	127.66	104.17	99.607	84.831	79.861	69.937	63.44	54.88	48.68	9855	11528	12172	12156	11536	10925	9825
7.00E-04	148.94	126.5	108.75	90.978	89.835	78.104	72.31	65.42	56.57	11132	13151	13648	13713	13071	12137	11344
6.00E-04	162.68	130.62	130.22	110.21	116.46	92.433	84.61	69.46	65.01	12761	15030	15673	15651	15028	13604	13076
5.00E-04	189.47	180.57	144.75	131.57	119.62	116.82	86.92	91.66	70.08	15047	17715	18426	18400	17530	16376	15252

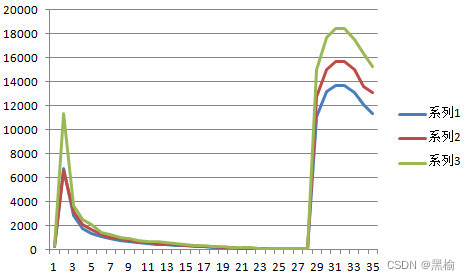
迭代次数的标准差有一个峰一个谷。n=5时为峰，n=320时为谷。

当n>320以后网络性能变得不再稳定，不统计，则这个网络的的收敛过程被一个峰值一个谷值分成3部分，2-5寻求平衡，5-320平衡，n>320，超出性能极限。

这个网络1-0位置的最大分类准确率为n=320时的65.8%。这个值更接近63.5%，所以有理由认为这个网络的峰值分类准确率就是63.5%，（0，0）时序优先，先到全得，（1，1）被对半分，但是当n=320时（0，0）的比例为3.97，（1，1）的比例为5.03，表明有过多的（1，1）被分为A这与（1，1）被对半分的假设相差巨大。

所以网络的最优节点数应该是120个或2个。此时网络的分类行为与训练集内在的分类逻辑最接近。