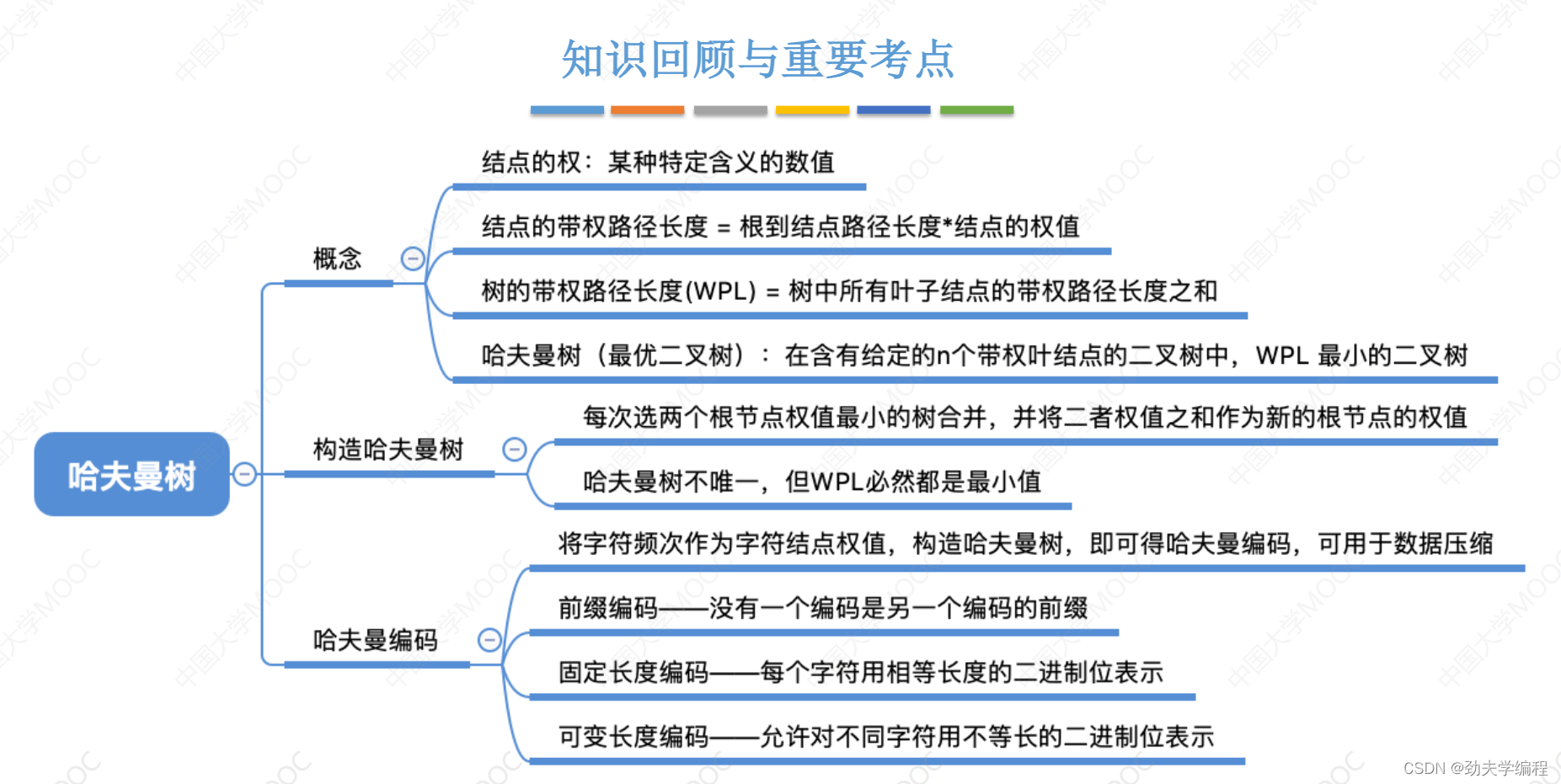
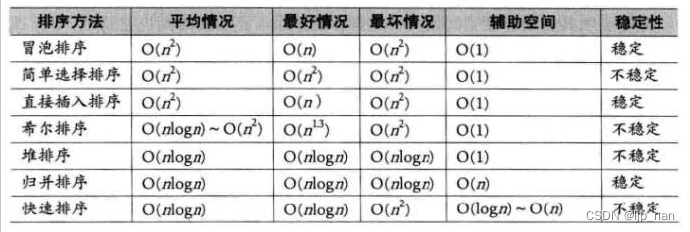
我总是在思考一个问题,为什么现在越来越多的人选择使用记事本app?它们相比传统笔记本,又有什么吸引人的地方呢?这其实并不难理解。因为,记事本app不仅可以让我们及时记录重要信息,还能对这些信息进行系统、规范的管理,以便于后续的查阅。既然如此,那么在移动智能化应用飞速发展的今天,究竟有哪些好用的记事本app可以用来整理个人笔记呢?
敬业签就能满足需求。它是一款功能强、空间大且易操作的记事本app,不仅能让我们用文字、录音、拍照等便签记事方式记录个人笔记,还可以在每篇便签笔记中上传图片、视频及文档等文件。这样一来,我们就能收集更多有用的信息,以供后续的借鉴和使用。

并且,敬业签的分类管理功能也非常的出色。可以让我们创建多个不同名称的分类标签,用于对同一性质或用途笔记的管理。同时,每个便签分类下都能容纳500篇笔记,而每篇笔记中还可以添加大量的文本及文件。所以,在敬业签的协助下,我们便能积攒更多的信息,来丰富自己的学识和能力。
此外,敬业签也是一款可以在Android、HarmonyOS以及ios等设备上同步使用的记事本app。这意味着,无论我们在哪个手机设备上使用它,只需联网登录同一账号,就可以同步查看到之前记录在这款记事本app中的内容。
总之,敬业签是一款既好用又适合用来整理个人笔记的记事本app。不管是对于学生、上班族还是任何需要整理个人笔记的人来说,它都能提供非常好的帮助。如果你也在寻找一款好用的记事本app,那么我强烈推荐你试试敬业签。